Projections
Maintenant que nous avons décrit le concept de réduction de dimension et certaines des applications de l’UDS et de l’analyse en composantes principales, nous nous concentrons sur plus de détails liés aux mathématiques qui les sous-tendent. Nous commençons par les projections. Une projection est un concept d’algèbre linéaire qui nous aide à comprendre un grand nombre des opérations mathématiques que nous effectuons sur des données en haute dimension. Pour plus de détails, vous pouvez examiner les projections dans un livre d’algèbre linéaire. Ici, nous fournissons un examen rapide, puis nous fournissons quelques exemples liés à l’analyse de données.
En guise d’examen, rappelez-vous que les projections minimisent la distance entre les points et le sous-espace.

Dans la figure ci-dessus, le point en haut pointe vers un point dans l’espace. Dans cette caricature particulière, l’espace est à deux dimensions, mais nous devrions penser de manière abstraite. L’espace est représenté par le plan cartésien et la ligne sur laquelle se tient la petite personne est un sous-espace de points. La projection dans ce sous-espace est l’endroit qui est le plus proche du point d’origine. La géométrie nous dit que nous pouvons trouver ce point le plus proche en traçant une ligne perpendiculaire (ligne pointillée) du point à l’espace. La petite personne se tient sur la projection. La quantité que cette personne a dû marcher de l’origine au nouveau point projeté est appelée la coordonnée.
Pour l’explication des projections, nous utiliserons la notation standard d’algèbre matricielle pour les points : est un point dans un espace à -dimension et est plus petit sous-espace.
Exemple simple avec N=2
Si nous laissons . Nous pouvons le tracer comme suit :
mypar (1,1)plot(c(0,4),c(0,4),xlab="Dimension 1",ylab="Dimension 2",type="n")arrows(0,0,2,3,lwd=3)text(2,3," Y",pos=4,cex=3)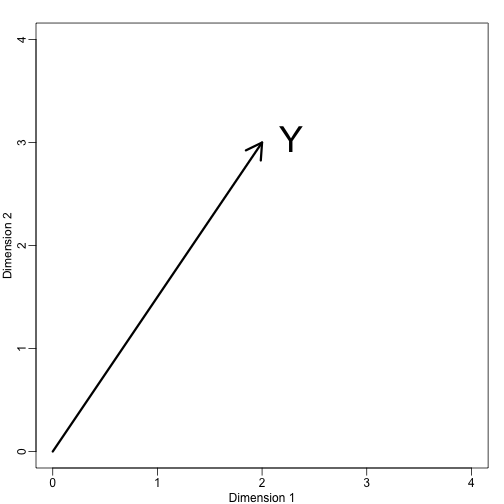
Nous pouvons immédiatement définir un système de coordonnées en projetant ce vecteur sur l’espace défini par : (l’axe des x) et (l’axe des y). Les projections de sur le sous-espace défini par ces points sont respectivement 2 et 3 :
Nous disons que et sont les coordonnées et que sont les bases.
Définissons maintenant un nouveau sous-espace. La ligne rouge dans le tracé ci-dessous est le sous-ensemble défini par les points satisfaisant à . La projection de sur est le point le plus proche de . Nous devons donc trouver le qui minimise la distance entre et . En algèbre linéaire, on apprend que la différence entre ces points est orthogonale à l’espace donc :
cela implique que :
et :
Ici le point représente le produit scalaire : .
Le code R suivant confirme que cette équation fonctionne :
mypar(1,1)plot(c(0,4),c(0,4),xlab="Dimension 1",ylab="Dimension 2",type="n")arrows(0,0,2,3,lwd=3)abline(0,0.5,col="red",lwd=3) #if x=2c and y=c then slope is 0.5 (y=0.5x)text(2,3," Y",pos=4,cex=3)y=c(2,3)x=c(2,1)cc = crossprod(x,y)/crossprod(x)segments(x*cc,x*cc,y,y,lty=2)text(x*cc,x*cc,expression(hat(Y)),pos=4,cex=3)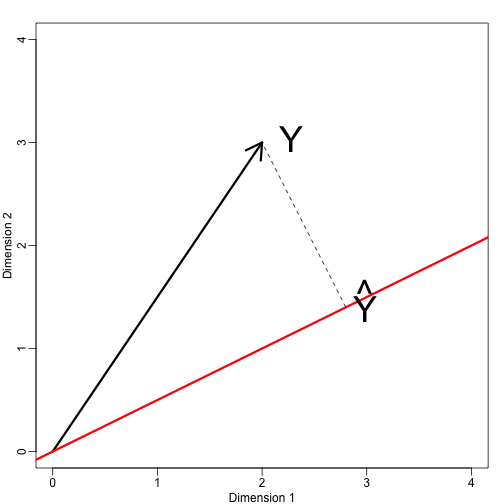
Notez que si était tel que , alors est simplement et l’espace ne change pas. Cette simplification est une des raisons pour lesquelles nous aimons les matrices orthogonales.
Exemple : La moyenne de l’échantillon est une projection
Let et est l’espace couvert par :
Dans cet espace, toutes les composantes des vecteurs ont le même nombre, on peut donc penser que cet espace représente les constantes : dans la projection, chaque dimension aura la même valeur. Donc, qu’est-ce qui minimise la distance entre et ?
Lorsque nous parlons de problèmes comme celui-ci, nous utilisons parfois des figures à 2 dimensions comme celle ci-dessus. Nous abstrayons simplement et pensons à comme un point dans et comme un sous-espace défini par un plus petit nombre de valeurs, dans ce cas une seule : ,
Pour en revenir à notre question, nous savons que la projection est :
ce qui dans ce cas est la moyenne :
Ici, il aurait également été tout aussi facile d’utiliser le calcul :
Exemple : La régression est aussi une projection
Donnons un exemple un peu plus compliqué. La régression linéaire simple peut aussi s’expliquer par des projections. Nos données (nous n’allons plus utiliser la notation) sont à nouveau un vecteur et notre modèle prédit avec une ligne . We want to find the and that minimize the distance between and the space defined by:
with:
Our matrix is and any point in can be written as .
The equation for the multidimensional version of orthogonal projection is:
which we have seen before and gives us:
And the projection to is therefore: