MO elmélet és konjugált pi-kötések
A szerves molekulák kötéseinek megértéséhez az MO elmélet használatának előnye még nyilvánvalóbbá válik, ha a pi-kötésekre gondolunk. Nézzük először az eténben lévő pi-kötést MO-elméleti szempontból (ebben a példában figyelmen kívül hagyjuk a molekulában lévő s-kötéseket, és csak a π-kötésre gondolunk). Két atomi orbitálból indulunk ki: mindkét szénből egy-egy hibridizálatlan 2p orbitál. Mindkettő egy-egy elektront tartalmaz. A MO-elméletben a két atomi matematikailag két pi molekuláris orbitált alkot, egy alacsony energiájú pi kötési orbitált és egy magas energiájú pi* antikötési orbitált.
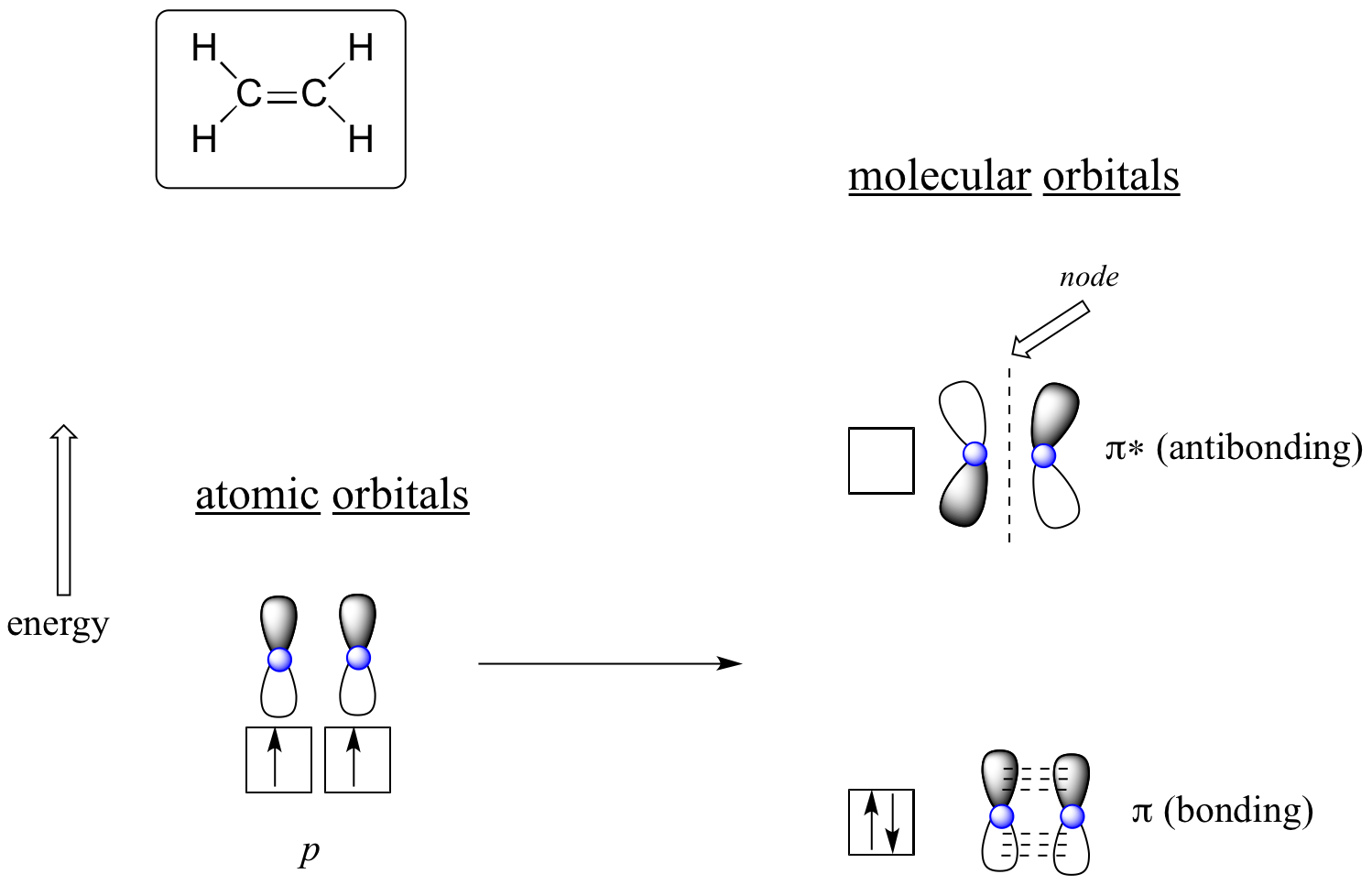
Etén (etilén)
A kötő pi-orbitálon a p-orbitálok két árnyékolt nyalábja konstruktív kölcsönhatásba lép egymással, akárcsak a két árnyékolatlan nyaláb (ne feledjük, az önkényesen választott árnyékolás a matematikai (+) és (-) jeleket jelenti az orbitált leíró matematikai hullámfüggvényben). A molekuláris orbitálisban a két szénatommag között megnövekedett elektronsűrűség van – ez egy kötési kölcsönhatás.
A magasabb energiájú antibonding pi* orbitálisban az egyik p orbitális árnyékolt nyalábja destruktív kölcsönhatásba lép a második p orbitális árnyékolatlan nyalábjával, ami csomópontot eredményez a két atommag között és általános taszítást a szénatommagok között.
Az “építkezés” elvét alkalmazva ismét a két elektront az alacsonyabb energiájú, kötő pi molekuláris orbitálba helyezzük. Az antibonding pi* orbitál üresen marad.
A következőkben az 1,3-butadién molekulát vizsgáljuk meg. Pusztán a valencia-orbitális elmélet alapján azt várhatnánk, hogy ebben a molekulában a C2-C3 kötés, mivel ez egy szigma kötés, szabadon foroghat.

Kísérleti úton azonban megfigyelhető, hogy a C2-C3 kötés körüli forgásnak jelentős akadálya van, és az egész molekula síkban van. Ráadásul a C2-C3 kötés 148 pm hosszú, rövidebb, mint egy tipikus szén-szén egyszerű kötés (kb. 154 pm), bár hosszabb, mint egy tipikus kettős kötés (kb. 134 pm).
A molekuláris orbitális elmélet a delokalizált pi-kötések fogalmával magyarázza ezeket a megfigyeléseket. Ebben a képben a négy 2p atomi pálya matematikailag négy növekvő energiájú pi molekuláris pályává egyesül. Ezek közül kettő – a kötő pi-orbitálok – alacsonyabb energiájú, mint a p atomi pályák, amelyekből kialakultak, míg kettő – az antibonding pi*-orbitálok – magasabb energiájúak.

A legalacsonyabb energiájú molekuláris pálya, a pi1, csak konstruktív kölcsönhatással és nulla csomóponttal rendelkezik. A magasabb energiájú, de még mindig alacsonyabb, mint az izolált p orbitálok, a pi2 orbitálnak egy csomópontja van, de két konstruktív kölcsönhatása – így összességében még mindig kötő orbitál. Ha a két antibonding orbitált nézzük, a pi3*-nak két csomópontja és egy konstruktív kölcsönhatása van, míg a pi4*-nek három csomópontja és nulla konstruktív kölcsönhatása van.
Az aufbau-elv szerint az izolált 2pz atomi orbitálok négy elektronja a kötő pi1 és pi2 MO-ba kerül. Mivel a pi1 konstruktív kölcsönhatást tartalmaz a C2 és C3 között, az 1,3-butadién molekulában bizonyos fokú pi-kötéses kölcsönhatás van e két szénatom között, ami a molekula rövidebb hosszát és a forgási gátat magyarázza. Az 1,3-butadién valenciakötéses képe a két pi-kötést egymástól elszigetelten mutatja, ahol minden pi-elektronpár a saját pi-kötésében “ragadt”. A molekuláris orbitális elmélet azonban (pontosan) azt jósolja, hogy a négy pi-elektron bizonyos mértékig delokalizáltan, azaz az egész pi-rendszerben “szétszórva” helyezkedik el.
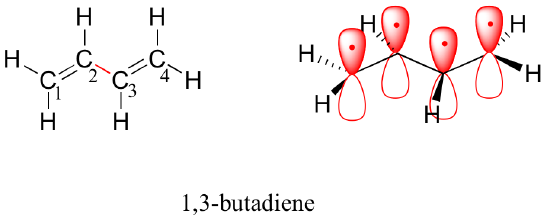
térkitöltő nézet
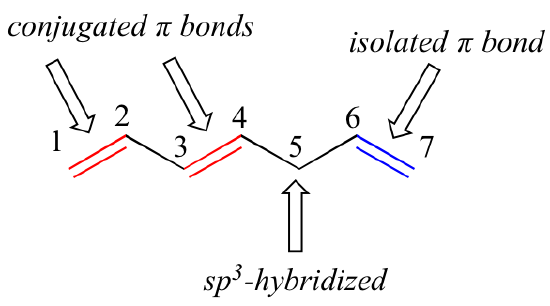
Az 1,3-butadién a legegyszerűbb példa a konjugált pi-kötések rendszerére. Ahhoz, hogy konjugáltnak tekintsük, két vagy több pi-kötést csak egyetlen kötésnek kell elválasztania egymástól – más szóval, nem lehet közte egy sp3-hibridizált szén, mert az felbontaná a párhuzamos p-orbitálisok átfedő rendszerét. Az alábbi vegyületben például a C1-C2 és C3-C4 kettős kötések konjugáltak, míg a C6-C7 kettős kötést az sp3-hibridizált C5 választja el a másik két pi-kötéstől.
Egy nagyon fontos fogalom, amit szem előtt kell tartanunk, hogy a konjugációnak van egy eredendő termodinamikai stabilitása. Ez a stabilitás kísérletileg mérhető két különböző dén hidrogénezési hőjének összehasonlításával. (A hidrogénezés egy olyan reakciótípus, amelyről a 15. fejezetben sokkal többet fogunk megtudni: lényegében egy hidrogénmolekula – két proton és két elektron – hozzáadása egy p-kötéshez). Amikor az 1,3-pentadién két konjugált kettős kötését “hidrogénezve” pentán keletkezik, a keletkező pentán egy móljára körülbelül 225 kJ szabadul fel. Hasonlítsuk ezt össze azzal a körülbelül 250 kJ/mol felszabaduló energiával, amely az 1,4-pentadién két izolált kettős kötésének hidrogénezésekor keletkezik, szintén pentánt képezve.
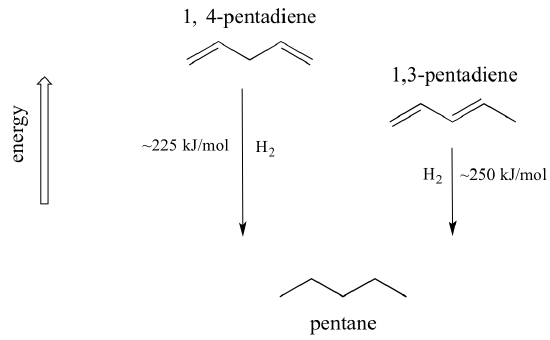
A konjugált diénnek alacsonyabb az energiája: más szóval stabilabb. Általában a konjugált pi-kötések stabilabbak, mint az izolált pi-kötések.
A konjugált pi-rendszerekben a szén mellett oxigén- és nitrogénatomok is részt vehetnek. A zsírmolekulák anyagcseréjében a kulcsreakciók némelyikében karbonilcsoportokhoz konjugált alkének vesznek részt.

A 4. fejezetben látni fogjuk, hogy az MO-elmélet nagyon hasznos annak magyarázatában, hogy a konjugált pi-kötések kiterjedt rendszereit tartalmazó szerves molekulák miért rendelkeznek gyakran jellegzetes színnel. A béta-karotin, a sárgarépa narancssárga színéért felelős vegyület 11 konjugált pi-kötésből álló kiterjedt rendszerrel rendelkezik.
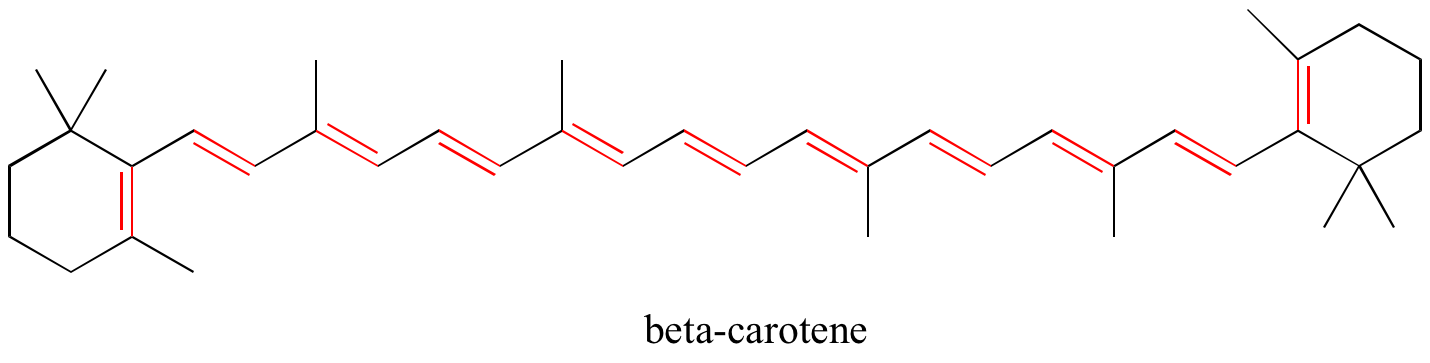
GYakorlat: Azonosítsa az összes konjugált és izolált kettős kötést az alábbi szerkezetekben. Adja meg minden egyes konjugált pi-rendszer esetében az átfedő p-orbitálisok számát, és azt, hogy hány pi-elektron osztozik közöttük.
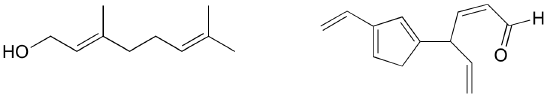
GYakorlat: Azonosítsd az összes izolált és konjugált pi-kötést a likopinban, a paradicsomban található piros színű vegyületben. Hány pi-elektron található a konjugált pi-rendszerben?

A feladatok megoldása
Aroma – A végső konjugált rendszer
A molekuláris orbitális elmélet különösen hasznos az aromás vegyületek, például a benzol egyedi tulajdonságainak magyarázatában:
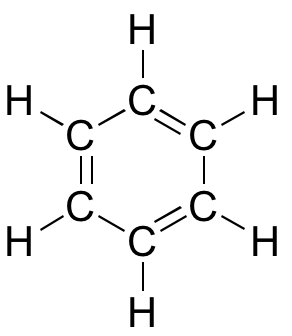
A benzol 3D interaktív modellje
Bár a benzolt leggyakrabban három kettős kötéssel és három egyszerű kötéssel rajzolják, valójában az összes szén-szén kötés pontosan ugyanolyan hosszú (138 pm). Ráadásul a benzolban lévő pi-kötések lényegesen kevésbé reaktívak, mint a “normál” pi-kötések, akár izoláltan, akár konjugáltan. A benzol szerkezetében van valami, ami a pi-kötések elrendezését különösen stabillá teszi. Ennek a “valaminek” neve is van: “aromásságnak” nevezik.
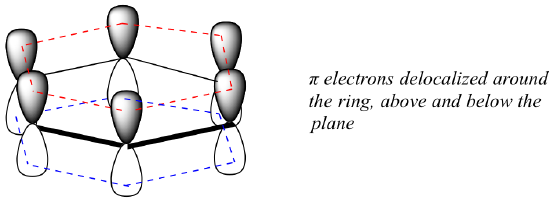
Mi pontosan ez az “aromás” tulajdonság, ami a benzolban lévő pi-kötéseket olyan stabilvá teszi? A kérdésre adott válasz nagyrészt abban rejlik, hogy a benzol egy ciklikus molekula, amelyben a gyűrű összes atomja sp2-hibridizált. Ez lehetővé teszi, hogy a pi-elektronok olyan molekuláris pályákon delokalizálódjanak, amelyek a gyűrű körül, a sík felett és alatt húzódnak. Ehhez természetesen a gyűrűnek síknak kell lennie – különben a p-orbitálisok nem tudnának megfelelően átfedni. A benzolról valóban ismert, hogy sík molekula.
Minden ciklikus, váltakozó egyszerű és kettős kötéssel rendelkező molekulának ugyanez az aromás stabilitása? A válasz valójában nem. Az alább látható nyolctagú ciklooktatetraén gyűrű nem lapos, és π-kötései úgy reagálnak, mint a “normál” alkének.
Az aromássághoz egyértelműen több kell, és ezt a molekuláris orbitálelmélettel lehet a legjobban megmagyarázni. Nézzük meg a benzol pi molekuláris pályáinak energiadiagramját.
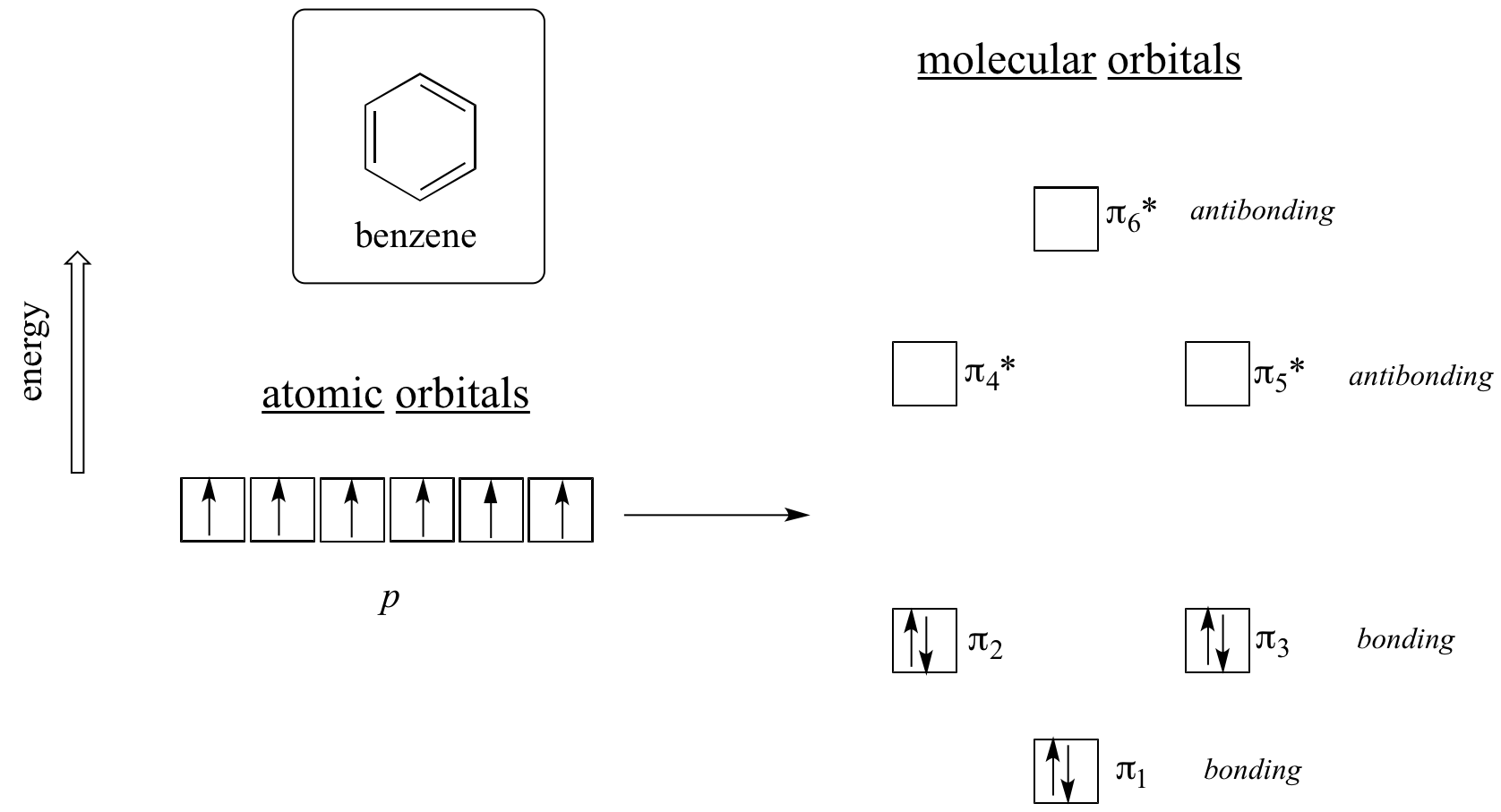
A kvantummechanikai számítások szerint a benzol hat pi molekuláris pályája, amely hat atomi p pályából alakul ki, négy külön energiaszintet foglal el. A pi1 és a pi6* egyedi energiaszintekkel rendelkeznek, míg a pi2 – pi3 és a pi4*- pi5* párok degeneráltak, vagyis ugyanazon az energiaszinten helyezkednek el. Ha az Aufbau-elv segítségével feltöltjük ezeket a pályákat a benzolban lévő hat pi-elektronnal, azt látjuk, hogy a kötési pályák teljesen kitöltöttek, az antibkötési pályák pedig üresek. Ez jó támpontot ad a benzol különleges stabilitásának forrására: a kötési MO-k teljes készlete sok tekintetben hasonlít a stabil nemesgázok, a hélium, a neon és az argon atomi pályáinak “teljes héjú” elektronjaihoz.
Most tegyük ugyanezt a ciklooktatetraén esetében, amelyről már megtudtuk, hogy nem aromás.
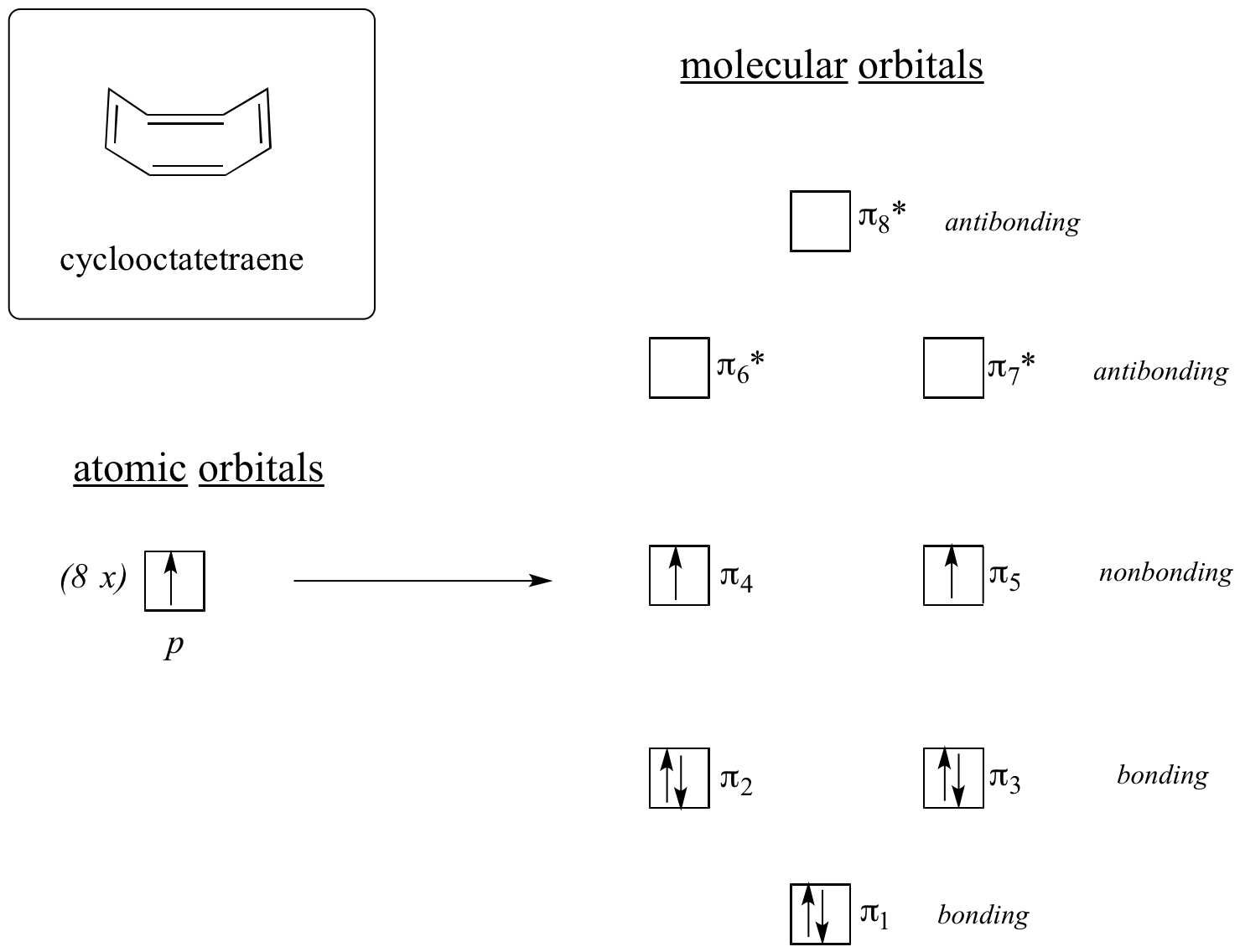
A molekuláris orbitális számítások eredménye azt mutatja, hogy a legalacsonyabb és legmagasabb energiájú MO-k (pi1 és pi8*) egyedi energiaszintekkel rendelkeznek, míg a többi hat elfajult párokat alkot. Vegyük észre, hogy a pi4 és pi5 ugyanazon az energiaszinten van, mint az izolált 2pz atomi pályák: ezek tehát sem nem kötő, sem nem antikötő, inkább nem kötő MO-knak nevezzük őket. A MO-kat a molekula nyolc pi elektronjával feltöltve azt találjuk, hogy az utolsó két elektron párosítatlan, és a két degenerált, nem kötő pályára esik. Mivel nincs tökéletesen kitöltött kötő MO-héj, a molekulánk nem aromás. Ennek következtében a ciklooktatetraénben minden egyes kettős kötés inkább úgy viselkedik, mint egy izolált kettős kötés.
Előre a fontos tanulási cél a konjugált pi-kötésrendszerek felismerése és annak megértése, hogy a benzol kivételesen stabil, és az aromásságnak nevezett tulajdonságot mutatja. Az aromásság és az aromás vegyületek kémiája viszonylag összetett, és a szöveg későbbi fejezeteiben részletesebben tárgyaljuk.
Organic Chemistry With a Biological Emphasis by Tim Soderberg (University of Minnesota, Morris)