Az \(\mu_{Y}\) konfidenciaintervallumának tárgyalásakor a képlet segítségével megvizsgáltuk, hogy milyen tényezők befolyásolják a konfidenciaintervallum szélességét. Nincs szükség arra, hogy ezt megismételjük. Mivel a képletek nagyon hasonlóak, kiderül, hogy az előrejelzési intervallum szélességét befolyásoló tényezők azonosak a konfidenciaintervallum szélességét befolyásoló tényezőkkel.
Vizsgáljuk meg ehelyett az \(y_{új}\) előrejelzési intervallumára vonatkozó képletet:
\(\hat{y}_h \pm t_{(1-\alpha/2, n-2)} \times \sqrt{MSE \times \left( 1+\dfrac{1}{n} + \dfrac{(x_h-\bar{x})^2}{\sum(x_i-\bar{x})^2}\right)}\)
hogy lássuk, hogyan viszonyul ez az \(\mu_{Y}\) konfidenciaintervallumának képletéhez:
\(\hat{y}_h \pm t_{(1-\alpha/2, n-2)} \times \sqrt{MSE \left(\dfrac{1}{n} + \dfrac{(x_h-\bar{x})^2}{\sum(x_i-\bar{x})^2}\right)}\)
Figyeljük meg, hogy az egyetlen különbség a képletekben az, hogy az \(y_{new}\) előrejelzés standard hibája tartalmaz egy extra MSE kifejezést, míg az \(\mu_{Y}\) illesztés standard hibája nem.
Próbáljuk megérteni az előrejelzési intervallumot, hogy lássuk, mi okozza az extra MSE-termet. Ennek során kezdjük először egy egyszerűbb problémával. Gondoljunk arra, hogyan tudnánk megjósolni egy új választ \(y_{new}\) egy adott \(x_{h}\) időpontban, ha a válaszok \(\mu_{Y}\) átlaga \(x_{h}\) időpontban ismert lenne. Vagyis tegyük fel, hogy ismert, hogy a bőrrákos halálozás átlaga \(x_{h} = 40^{o}\) N-nél 150 halálozás millióra (400-as szórással)? Mekkora az előre jelzett bőrrákos halálozás az ohiói Columbusban?
Mivel \(\mu_{Y} = 150 \) és \( \sigma^{2} = 400\) ismert, kihasználhatjuk az “empirikus szabályt”, amely többek között azt mondja ki, hogy a normális eloszlású adatok méréseinek 95%-a az átlag 2 szórásán belül van. Ez azt jelenti, hogy a mérések 95%-a a következő intervallumok közé esik:
\(\mu_{Y}- 2\sigma\) és \(\mu_{Y}+ 2\sigma\).
A 95%-os szabályt alkalmazva példánkra \(\mu_{Y} = 150\) és \(\sigma= 20\):
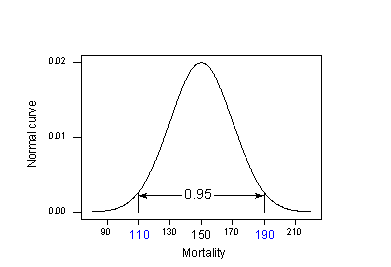
A bőrrák halálozási arányának 95%-a az északi szélesség 40. fokán fekvő helyeken a következő intervallumba esik:
150 – 2(20) = 110 és 150 + 2(20) = 190 között.
Ez azt jelenti, hogy ha valaki tudni szeretné a bőrrák halálozási arányát az északi szélesség 40. fokán fekvő helyeken, a legjobb becslésünk szerint valahol 110 és 190 haláleset között lenne 10 millióra vetítve. A probléma az, hogy a számításunkban \(\mu_{Y}\) és \(\sigma\) népességi értékeket használtunk, amelyeket általában nem ismerünk. A valóságban:
- Az \(\mu_{Y}\) átlaga jellemzően nem ismert. A logikus az lenne, ha a megjósolt válasz \(\hat{y}\) segítségével becsülnénk meg. Az \(\hat{y}\) felhasználásának költsége az \(\mu_{Y}\) becsléséhez az \(\hat{y}\) szórása. Ez azt jelenti, hogy különböző minták különböző előrejelzéseket adnának \(\hat{y}\), és ezért figyelembe kell vennünk \(\hat{y}\) ezen varianciáját.
- Az \( \sigma^{2}\) varianciája általában nem ismert. Logikusan az MSE-vel kell becsülni.
Mivel ezeket az ismeretlen mennyiségeket meg kell becsülnünk, az új válasz előrejelzésének szórása két komponenstől függ:
- az \(\mu_{Y}\) átlag \(\hat{y}_h\) becsléséből adódó szórás, amelyet “\(\sigma^2(\hat{Y}_h)\)”-nek jelölünk.” (Megjegyezzük, hogy ennek a mennyiségnek a becslése nem más, mint az illeszkedés standard hibájának négyzete, amely a konfidenciaintervallum képletében szerepel.)
- az y válaszok szórása, amelyet “\(\sigma^2\)”-ként jelölünk.” (Megjegyezzük, hogy a mennyiséget a szokásos módon az MSE átlagos négyzetes hibával becsüljük.)
A két varianciakomponenst összeadva megkapjuk:
\(\sigma^2+\sigma^2(\hat{Y}_h)\)
amelyet a következő módon becsülünk:
\(MSE+MSE \left( \dfrac{1}{n} + \dfrac{(x_h-\bar{x})^2}{\sum_{i=1}^{n}(x_i-\bar{x})^2} \right) =MSE\left( 1+\dfrac{1}{n} + \dfrac{(x_h-\bar{x})^2}{\sum_{i=1}^{n}(x_i-\bar{x})^2} \right) \)
Megismeri ezt a mennyiséget? Ez nem más, mint az előrejelzés varianciája, amely az \(y_{új}\) előrejelzési intervallum képletében szerepel!
Hasonlítsuk össze újra a két intervallumot:
Az \(\mu_{Y}\colon \hat{y}_h \pm t_{(1-\alpha/2, n-2)} bizalmi intervalluma \times \sqrt{MSE \times \left( \frac{1}{n} + \frac{(x_h-\bar{x})^2}{\sum(x_i-\bar{x})^2}\right)}\)}\)
Prediction interval for \(y_{new}\colon \hat{y}_h \pm t_{(1-\alpha/2, n-2)} \times \sqrt{MSE \left( 1+\frac{1}{n} + \frac{(x_h-\bar{x})^2}{\sum(x_i-\bar{x})^2}\right)}\)}\)
Mi a gyakorlati következménye a két képlet közötti különbségnek?
- Mivel az előrejelzési intervallum tartalmazza az extra MSE-termet, az \(x_{h}\) \( \left( 1-\alpha \right) 100\% \) konfidenciaintervallum \(\mu_{Y}\) esetén mindig szűkebb lesz, mint a megfelelő \( \left( 1-\alpha \right) 100\% \) előrejelzési intervallum \(y_{new}\) esetén \(x_{h}\).
- Az \(\left(x_{h} = \bar{x}\right)\) prediktorértékek mintaátlagánál számított intervallum kiszámításával és az n mintaméret növelésével a konfidenciaintervallum standard hibája megközelítheti a 0-t. Mivel a predikciós intervallum rendelkezik az extra MSE kifejezéssel, a predikciós intervallum standard hibája nem kerülhet közel a 0-hoz.
Az első implikáció legkönnyebben a bőrrákos halálozási példánk alábbi diagramjának tanulmányozásával látható:
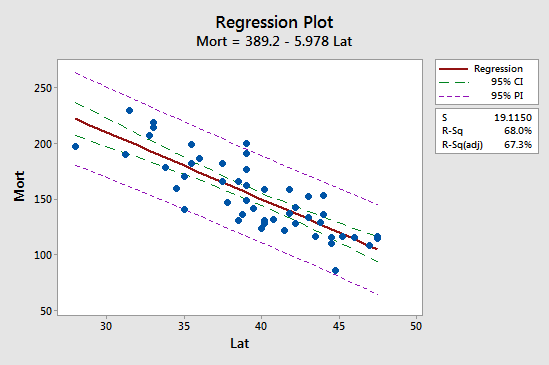
Nézzük meg, hogy az előrejelzési intervallum (95% PI, lila színnel) mindig szélesebb, mint a konfidenciaintervallum (95% CI, zöld színnel). Továbbá mindkét intervallum a prediktív értékek átlagánál (kb. 39,5) a legszűkebb.