A mágikus négyzetek olyan négyzetrácsok, amelyekben a számok különleges elrendezése található. Ezek a számok azért különlegesek, mert minden sor, oszlop és átló ugyanazt a számot adja ki. Az alábbi példában tehát a 15 a mágikus szám. Ki tudod ezt számolni pusztán abból, hogy tudod, hogy a négyzet az 1-től 9-ig terjedő számokat használja?

Az a két szám, amely a középső számmal szemben áll, szintén ugyanazt a számot adja ki. Tehát a fenti négyzetben 8 + 2 = 10 , 6 + 4 = 10, 1 + 9 = 10 és 3 + 7 = 10. Miért van ez?
A bűvös négyzet “sorrendje” megadja, hogy hány sora vagy oszlopa van. Tehát egy 3 soros és 3 oszlopos négyzet a 3-as rend, egy 4 soros és 4 oszlopos négyzet a 4-es rend, és így tovább. Ha többet szeretnél megtudni arról, hogyan állítsd össze a saját mágikus négyzeteidet, és a mögötte álló matematikáról, akkor látogass el a honlap néhány más oldalára, például a Varázsnégyzetek és a Varázsnégyzetek II.
De miért hívják őket mágikusnak?
A mágikus négyzetben lévő számok tehát különlegesek, de miért hívják őket mágikusnak? Úgy tűnik, hogy az ősi idők óta a természetfeletti és mágikus világhoz kapcsolódnak. A legkorábbi feljegyzés a mágikus négyzetekről Kínából származik, i.e. 2200 körülről, és “Lo-Shu” néven szerepel. Egy legenda szerint Yu császár látta ezt a mágikus négyzetet egy isteni teknős hátán a Sárga-folyóban.
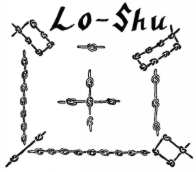
A fekete csomók páros számokat, a fehér csomók pedig páratlan számokat jeleznek. Nézd meg jobban, és látni fogod, hogy ez az ősi mágikus négyzet megegyezik a fenti példánkkal. A mágikus négyzeteket a nyugati világban először a szmirnai Theon munkájában említik. A 9. században arab asztrológusok is használták őket, hogy segítsenek a horoszkópok kidolgozásában. A görög matematikus, Moschopoulos munkája i.sz. 1300-ban segít elterjeszteni a mágikus négyzetekről szóló ismereteket. Így most itt vagyunk, több mint 700 évvel később, és a tanárok használják őket az órákon problémamegoldásra és az összeadás gyakorlására.
Hasonló mágikus négyzeteket készíthetsz, 3-as nagyságrendben, különböző számok felhasználásával. Látsz valamilyen mintát a számok között, ami működik?