Ebben a részben megtanuljuk, hogyan találjuk meg egy kvadratikus egyenlet gyökét (gyökeit). A gyököket x-intervallumoknak vagy nullpontoknak is nevezik. Egy kvadratikus függvényt grafikusan egy parabola ábrázol, amelynek csúcsa az origóban, az x-tengely alatt vagy az x-tengely felett helyezkedik el. Ezért egy kvadratikus függvénynek lehet egy, két vagy nulla gyöke.
Amikor egy kvadratikus egyenlet megoldását kérjük, valójában a gyökerek megtalálását kérjük. Már láttuk, hogy a négyzet kiegészítése hasznos módszer a kvadratikus egyenletek megoldására. Ezzel a módszerrel levezethetjük a kvadratikus képletet, amelyet a kvadratikus egyenletek megoldására használunk. Valójában a
f (x) = ax2 + bx + c
függvény gyökeit a kvadratikus képlet adja meg. A függvény gyökei az x metszéspontjai. Definíció szerint az x-tengelyen fekvő pontok y-koordinátája nulla. Ezért egy kvadratikus függvény gyökeit úgy találjuk meg, hogy f (x) = 0, és megoldjuk az
ax2 + bx + c = 0 egyenletet.
We can do this by completing the square as,
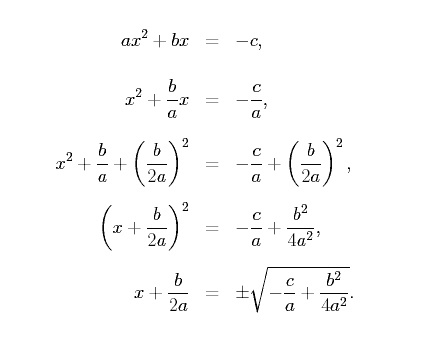
Solving for x and simplifying we have,
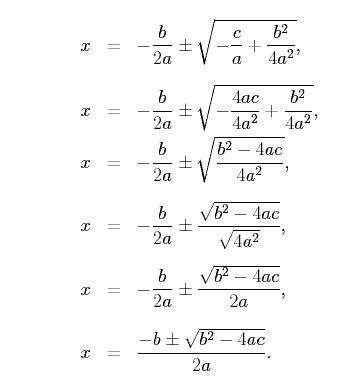
Thus, the roots of a quadratic function are given by,
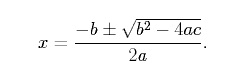
This formula is called the quadratic formula, and its derivation is included so that you can see where it comes from. We call the term b2 −4ac the discriminant. The discriminant is important because it tells you how many roots a quadratic function has. Specifically, if
1. b2 −4ac < 0 There are no real roots.
2. b2 −4ac = 0 There is one real root.
3. b2 −4ac > 0 There are two real roots.
We will examine each case individually.
1. eset: Nincsenek valós gyökök
Ha egy kvadratikus függvény diszkriminanciája kisebb nullánál, akkor a függvénynek nincsenek valós gyökei, és az általa ábrázolt parabola nem metszi az x-tengelyt. Mivel a kvadratikus képlethez a diszkriminancia négyzetgyökét kell venni, a negatív diszkriminancia problémát okoz, mivel a negatív számok négyzetgyöke nem definiált a valós egyenesen. Egy példa olyan kvadratikus függvényre, amelynek nincs valós gyöke, a következő:
f(x) = x2 – 3x + 4.
Megjegyezzük, hogy f(x) diszkriminanciája negatív,
b2 -4ac = (-3)2- 4 – 1 – 4 = 9 – 16 = -7.
Ezt a függvényt grafikusan egy felfelé nyíló parabola ábrázolja, amelynek csúcsa az x-tengely felett van. Így a grafikon soha nem metszheti az x-tengelyt, és nincs gyöke, ahogy az alábbiakban látható
2. eset: Egy valós gyök
Ha egy kvadratikus függvény diszkriminanciája egyenlő nullával, akkor a függvénynek pontosan egy valós gyöke van, és egyetlen pontban metszi az x-tengelyt. Hogy ezt lássuk, a kvadratikus képletben b2 -4ac = 0-t állítunk, így kapjuk:
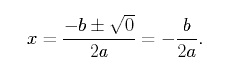
Vegyük észre, hogy 
a parabola csúcsának x-koordinátája. Tehát egy parabolának pontosan egy valós gyöke van, ha a parabola csúcsa pontosan az x-tengelyen fekszik. A legegyszerűbb példa a csak egy valós gyökkel rendelkező kvadratikus függvényre az,
y = x2,
ahol a valós gyök x = 0.
A másik példa az egy valós gyökkel rendelkező kvadratikus függvényre az,
f(x) = -4×2 + 12x – 9.
Vegyük észre, hogy f(x) diszkriminanciája nulla,
b2 -4ac = (12)2- 4 – -4 – -4 – -9 = 144 – 144 = 0.
Ezt a függvényt grafikusan egy lefelé nyíló parabola ábrázolja, amelynek csúcsa (3/2, 0), az x tengelyen fekszik. Thus, the graph intersects the x-axis at exactly one point (i.e. has one root) as shown below,
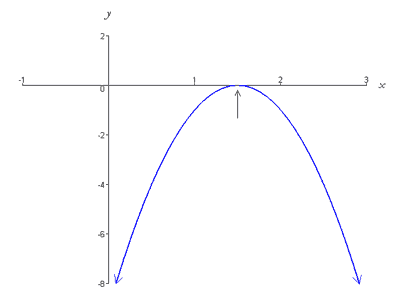
Case 3: Two Real Roots
If the discriminant of a quadratic function is greater than zero, that function has two real roots (x-intercepts). Taking the square root of a positive real number is well defined, and the two roots are given by,
An example of a quadratic function with two real roots is given by,
f(x) = 2×2− 11x + 5.
Notice that the discriminant of f(x) is greater than zero,