A Cobb-Douglas termelési függvény a termelési kibocsátás és a termelési inputok (tényezők) közötti kapcsolatot modellezi. A hatékony termelés érdekében az inputok egymáshoz viszonyított arányainak kiszámítására és a termelési módszerek technológiai változásának becslésére használják. A Cobb-Douglas termelési függvény általános formája \(n\) inputok halmazára a következő: \(Y\) a kibocsátást, \(x_{i}\) az \(i\) inputot, és \(\gamma\) és \(\alpha_{i}\) a termelés általános hatékonyságát és a kibocsátás reagálását az inputmennyiségek változásaira meghatározó paraméterek. Ennek a funkcionális formának a termelés mérésére való alkalmazása Charles Cobb matematikusnak és Paul Douglas közgazdásznak köszönhető, akik ezt a formát arra használták, hogy megvizsgálják a két ráfordítási tényező, a munka és a tőke relatív jelentőségét a feldolgozóipari termelésben az Egyesült Államokban az 1899 és 1922 közötti időszakban. Eredeti modelljükben Cobb és Douglas a \(\alpha_{1}\) és \(\alpha_{2}\) termelési rugalmassági paramétereket a \(\alpha_{i}\in\left(0,1\right)\) tartományra korlátozták, és összegük egy, ami állandó skálahozamot feltételez. A függvény tehát\ ahol \(x_{1}\) és \(x_{2}\) a munkát, illetve a tőkét jelöli. Ha az egyenlet mindkét oldalának természetes logaritmusát vesszük, akkor az \(\gamma\) és \(\alpha_{1}\) paraméterek a kibocsátásra, a munkára és a tőkére vonatkozó adatok esetében a szokásos legkisebb négyzetek segítségével becsülhetők. Adataik alapján Cobb és Douglas az \(\alpha_{1}\) 0,75-ös értékét találta, ami azt jelenti, hogy a vizsgált időszakban az amerikai feldolgozóipari termelés értékének háromnegyedét a munka adta (a fennmaradó negyedet a tőke). Az \(\gamma\) hatékonysági paraméterre vonatkozó becslésük 1,01, ami, mivel nagyobb, mint 1, a nem megfigyelhető erők pozitív hatását tükrözi a termelésre a munka és a tőke kombinációján keresztül.
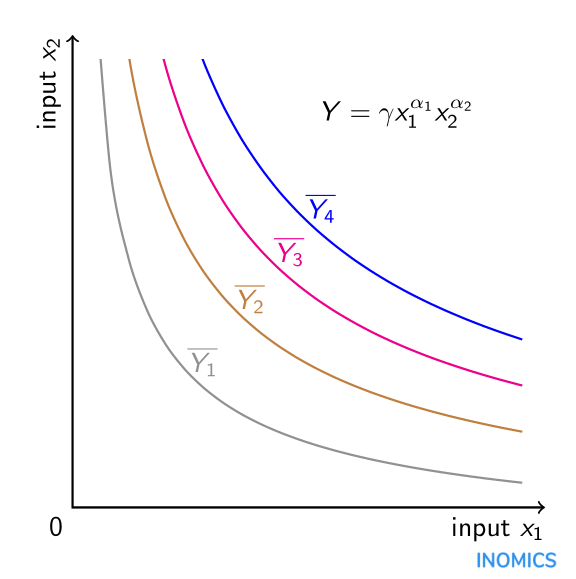
A Cobb-Douglas termelési függvény multiplikatív jellege, az \(\alpha_{i}\) pozitív értékeit feltételezve, azt jelenti, hogy az inputok kiegészítik egymást a termelésben. A munka és tőke standard modelljében a tőke mennyiségének növelése nemcsak közvetlenül növeli a termelést, hanem közvetve a munka termelékenységére gyakorolt hatásán keresztül közvetve is. Matematikailag a termelési kibocsátás \(Y\) keresztparciális deriváltja a munka \(x_{1}\) és a tőke \(x_{2}\) függvényében pozitív. Továbbá, annak a feltételezésnek köszönhetően, hogy \(\alpha_{i}\in\left(0,1\right)\), a termelési kibocsátás másodrendű parciális deriváltja a munka és a tőke tekintetében egyaránt negatív, ami azt jelenti, hogy az egyes ráfordítások határhozama csökken. Ha egyszerűen több munka vagy több tőke (de nem mindkettő) hozzáadása a termelési folyamathoz növeli a kibocsátást, bár csökkenő mértékben. Továbbá a funkcionális forma miatt a ráfordítások közötti helyettesítési rugalmasság állandó és egyenlő eggyel. A két inputból álló Cobb-Douglas termelési függvény grafikusan ábrázolható izoquantumok formájában: a két input olyan kombinációi, amelyek esetében a kibocsátás állandó. Az ábrán négy ilyen izoquantum található az \(\overline{Y_{1}}\), \(\overline{Y_{2}}\), \(\overline{Y_{3}}\) és \(\overline{Y_{4}}}\) (állandó) kibocsátási szintekre. Minél távolabb van az izokvantum az origótól, annál nagyobb az \(\overline{Y_{4}}>\overline{Y_{3}}>\overline{Y_{2}}}>\overline{Y_{1}}\). Azt, hogy az \(x_{1}\) és az \(x_{2}\) inputok melyik pontos kombinációja optimális a termeléshez, a termelő rendelkezésére álló költségvetés, valamint az \(x_{2}\) és az \(x_{1}\) input költségaránya határozza meg, amely a grafikonon izoköltségvonal formájában szerepelhet (lásd a helyettesítési rugalmasságról szóló cikket).
Cobb és Douglas maguk is elismerték, hogy termelési függvényük nem áll szilárd elméleti alapokon, és nem is szabad termelési törvényként értelmezni; csupán a termelési inputok és a kibocsátás között megfigyelt összefüggések statisztikai közelítését jelenti. Mindazonáltal egyszerű matematikai tulajdonságai vonzóak a közgazdászok számára, és ahhoz vezettek, hogy az elmúlt évszázadban a mikroökonómiai elmélet standardjává vált.
További olvasmányok:
A Cobb-Douglas termelési függvények hátterét és főbb tulajdonságainak áttekintését lásd különösen Cobb és Douglas eredeti cikkének, “A Theory of Production” (The American Economic Review, 1928) 6., 7. és 8. szakaszában.
Jó tudni:
A Cobb-Douglas-funkcióformát nemcsak a termeléselméletben használják, hanem a mikroökonómiai fogyasztóelméletben is szokássá vált, ahol hasznossági függvényként alkalmazzák, ahol \(Y\) \(U\) lesz a hasznosságból \(U\). Az \(x_{i}\) a fogyasztási tételeket jelenti, és ha a hasznossági függvényt egy költségvetési korlát mellett maximalizáljuk, akkor az \(\alpha_{i}\) értékek azt jelzik, hogy az egyén hogyan osztja el optimálisan a költségvetést a tételek között.