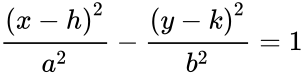by: adminPosted on:

Félnagytengely

Fájl:Félnagytengely.png

Az ellipszis félnagytengelye

A geometriában a félnagytengely (más néven félnagytengely) kifejezést az ellipszisek és hiperbolák méreteinek leírására használják.

Ellipszis

Az ellipszis nagytengelye az alakzat leghosszabb átmérője, a középponton és mindkét fókuszon átmenő egyenes, amelynek végei az alakzat legszélesebb pontjainál vannak. A félnagytengely a nagytengely egyik fele, tehát a középponttól egy fókuszon keresztül az ellipszis széléig fut.

A félnagytengellyel {\displaystyle b\,\!} az excentricitáson keresztül és a semi-latus rectum {\displaystyle \ell \,\!}, a következőképpen:

{\displaystyle b=a{\sqrt {1-e^{2}}}\,\!}{\displaystyle \ell =a(1-e^{2})\,\!}{\displaystyle a\ell =b^{2}\,\!}.

A parabola olyan ellipszisek sorozatának határértékeként kapható, ahol az egyik fókuszt fixen tartjuk, miközben a másik fókuszt tetszőlegesen messzire engedjük elmozdulni az egyik irányba, {\displaystyle \ell \,\!} fixen tartva. Így {\displaystyle a\,\!} és {\displaystyle b\,\!} a végtelenbe tendál, {\displaystyle a\,\!} gyorsabban, mint {\displaystyle b\,\!}.

A félnagytengely a legkisebb és legnagyobb távolságok középértéke az ellipszis egyik fókuszpontjától az ellipszis pontjaihoz képest. Tekintsük most az egyenletet polárkoordinátákban, ahol az egyik fókusz az origóban, a másik pedig a pozitív x-tengelyen van,

{\displaystyle r(1-e\cos \theta )=l\,\!}

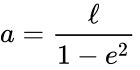
The mean value of {\displaystyle r={\ell \over {1+e}}\,\!} and {\displaystyle r={\ell \over {1-e}}\,\!}, is {\displaystyle a={\ell \over {1-e^{2}}}\,\!}.

Hyperbola

The semi-major axis of a hyperbola is one half of the distance between the two branches; if this is a in the x-direction the equation is:

{\displaystyle {\frac {\left(x-h\right)^{2}}{a^{2}}}-{\frac {\left(y-k\right)^{2}}{b^{2}}}=1}

In terms of the semi-latus rectum and the eccentricity we have

{\displaystyle a={\ell \over e^{2}-1}}

Astronomy

Orbital period

In astrodynamics the orbital period 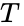{\displaystyle T\,} of a small body orbiting a central body in a circular or elliptical orbit is:

{\displaystyle T=2\pi {\sqrt {a^{3}/\mu }}}

where:

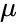
{\displaystyle a\,} a pálya félnagytengelyének hossza {\displaystyle \mu } a standard gravitációs paraméter

Megjegyezzük, hogy minden adott félnagytengellyel rendelkező ellipszis esetében a pálya periódusa az excentricitástól függetlenül azonos.

A csillagászatban a félnagytengely a pálya egyik legfontosabb keringési eleme, a keringési periódussal együtt. A Naprendszer objektumai esetében a félnagytengelyt Kepler harmadik (eredetileg empirikusan levezetett) törvénye kapcsolja össze a pálya időtartamával,

{\displaystyle T^{2}=a^{3}\,}

ahol T az időtartam években, a pedig a félnagytengely csillagászati egységekben. Ez a forma a Newton által meghatározott kéttest-probléma általános formájának egyszerűsítése:

{\displaystyle T^{2}={\frac {4\pi ^{2}}{G(M+m)}}a^{3}\,}

ahol G a gravitációs állandó, M a központi test tömege, m pedig a keringő test tömege. Általában a központi test tömege annyival nagyobb, mint a keringő testé, hogy m figyelmen kívül hagyható. Ha ezt feltételezzük, és a tipikus csillagászati mértékegységeket használjuk, akkor a Kepler által felfedezett egyszerűbb formát kapjuk.

Figyelemre méltó, hogy a keringő test pályája a barycentrum körül és az elsődleges testhez viszonyított pályája is ellipszis. A csillagászatban használt félnagytengely mindig a primer-szekunder távolságot jelenti; így a bolygók pályaparamétereit heliocentrikusan adjuk meg. A primocentrikus és az “abszolút” pályák közötti különbséget legjobban a Föld-Hold rendszerrel szemléltethetjük. A tömegarány ebben az esetben 81,30059. A Föld-Hold jellemző távolság, a geocentrikus holdpálya félnagytengelye 384 400 km. A barycentrikus holdpálya félnagytengelye ezzel szemben 379 700 km, a Föld ellenpályája a különbözetet, 4700 km-t veszi fel. A Hold átlagos barycentrikus keringési sebessége 1,010 km/s, míg a Földé 0,012 km/s. E sebességek összege adja a geocentrikus Hold átlagos keringési sebességét, 1,022 km/s; ugyanezt az értéket kaphatjuk, ha csak a geocentrikus félnagytengely értékét vesszük figyelembe.

Átlagos távolság

Sokszor mondják, hogy a félnagytengely az elsődleges (az ellipszis fókuszpontja) és a keringő test közötti “átlagos” távolság. Ez nem egészen pontos, mivel attól függ, hogy mi felett vesszük az átlagot.

  • A távolság átlagolása az excentrikus anomália (lásd még) felett valóban a félnagytengelyt eredményezi.
  • A valódi anomália (a fókuszban mért valódi keringési szög) feletti átlagolás furcsa módon a félkisebb tengelyt eredményezi {\displaystyle b=a{\sqrt {1-e^{2}}}}\,\\!}.
  • az átlagos anomália (a pericentrum óta eltelt keringési periódus szögben kifejezett hányada) átlagolása végül az időátlagot adja (a laikusok számára az “átlag” általában ezt jelenti): {\displaystyle a(1+{\frac {e^{2}}}{2}})\,\!}.

A sugár inverzének időbeli átlaga, {\displaystyle r^{-1}\,\!}{\displaystyle a^{-1}\,\!}.

Energia; a félnagytengely számítása az állapotvektorokból

Asztrodinamikában a félnagytengely {\displaystyle a\,} a pályaállapotvektorokból számítható:

{\displaystyle a={-\mu \over {2\epsilon }}\,} for an elliptical orbit and {\displaystyle a={\mu \over {2\epsilon }}\,} for a hyperbolic trajectory

and

{\displaystyle \epsilon ={v^{2} \over {2}}-{\mu \over \left|\mathbf {r} \right|}} (specific orbital energy)

and

{\displaystyle \mu =GM\,} (standard gravitational parameter),

where:

  • {\displaystyle v\,} is orbital velocity from velocity vector of an orbiting object,
  • {\displaystyle \mathbf {r} \,} is cartesian position vector of an orbiting object in coordinates of a reference frame with respect to which the elements of the orbit are to be calculated (e.g. geocentrikus egyenlítői a Föld körüli pálya esetén, vagy heliocentrikus ekliptikus a Nap körüli pálya esetén),
  • {\displaystyle G\,} a gravitációs állandó,
  • {\displaystyle M\,} a központi test tömege.

Megjegyezzük, hogy adott központi test és teljes fajlagos energia esetén a félnagytengely az excentricitástól függetlenül mindig azonos. Megfordítva, adott központi test és félnagytengely esetén a teljes fajlagos energia mindig azonos.

Példa

A Nemzetközi Űrállomás keringési ideje 91,74 perc, ezért a félnagytengelye 6738 km . Minden további perc kb. 50 km-rel többnek felel meg: a 300 km plusz pályahossz 40 másodpercet vesz igénybe, a kisebb sebesség további 20 másodpercet tesz ki.

Vélemény, hozzászólás?

Az e-mail-címet nem tesszük közzé. A kötelező mezőket * karakterrel jelöltük