Vetítések
Most, miután ismertettük a dimenziócsökkentés fogalmát, valamint az SVD és a főkomponens-elemzés néhány alkalmazását, a mögöttük álló matematikával kapcsolatos további részletekre összpontosítunk. A vetítésekkel kezdjük. A vetület egy lineáris algebrai fogalom, amely segít megérteni számos olyan matematikai műveletet, amelyet nagydimenziós adatokon végzünk. További részletekért a vetületeket egy lineáris algebrai könyvben tekintheti át. Itt egy gyors áttekintést nyújtunk, majd néhány adatelemzéssel kapcsolatos példát adunk.
Az áttekintéshez ne feledjük, hogy a vetületek minimalizálják a pontok és az altér közötti távolságot.

A fenti ábrán a fenti pont a tér egy pontjára mutat. Ebben a konkrét rajzfilmben a tér kétdimenziós, de absztrakt módon kell gondolkodnunk. A teret a kartéziánus sík ábrázolja, és a vonal, amelyen a kis emberke áll, a pontok egy résztér. Ennek az altérnek a vetülete az a hely, amelyik a legközelebb van az eredeti ponthoz. A geometria azt mondja, hogy ezt a legközelebbi pontot úgy találhatjuk meg, ha a pontból a térre merőleges egyenest (szaggatott vonal) húzunk. A kis emberke a vetületen áll. Azt az utat, amit ennek az emberkének az origótól az új vetített pontig meg kellett tennie, koordinátának nevezzük.
A vetületek magyarázatához a pontok szokásos mátrixalgebrai jelölését fogjuk használni: a pont a -dimenziós térben és a kisebb résztér.
Egyszerű példa N=2-vel
Ha hagyjuk, hogy . Ezt így ábrázolhatjuk:
mypar (1,1)plot(c(0,4),c(0,4),xlab="Dimension 1",ylab="Dimension 2",type="n")arrows(0,0,2,3,lwd=3)text(2,3," Y",pos=4,cex=3)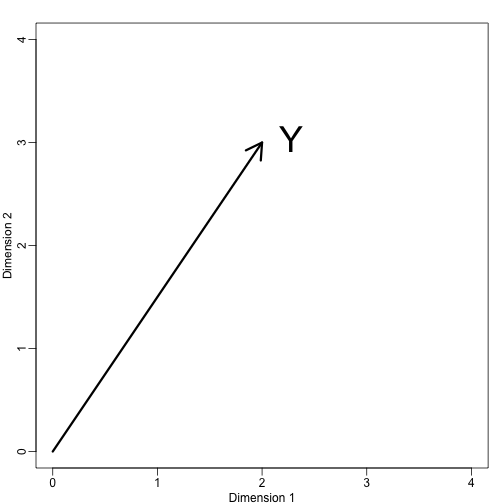
Ezt a vektort az által meghatározott térbe vetítve azonnal meghatározhatunk egy koordinátarendszert: (az x-tengely) és (az y-tengely). Az e pontok által definiált altérre való vetületek 2, illetve 3:
Mondjuk, hogy és a koordináták és hogy a bázisok.
Most definiáljunk egy új altérséget. Az alábbi ábrán látható piros vonal a pontok által definiált részhalmaz, amely kielégíti a . Az onto vetülete a legközelebbi pont a . Tehát meg kell találnunk azt, amely minimalizálja az és közötti távolságot. A lineáris algebrában megtanuljuk, hogy e pontok különbsége ortogonális a térre, tehát:
ez azt jelenti, hogy:
és:
Itt a pont a pontszorzatot jelenti: .
Az alábbi R-kód megerősíti, hogy ez az egyenlet működik:
mypar(1,1)plot(c(0,4),c(0,4),xlab="Dimension 1",ylab="Dimension 2",type="n")arrows(0,0,2,3,lwd=3)abline(0,0.5,col="red",lwd=3) #if x=2c and y=c then slope is 0.5 (y=0.5x)text(2,3," Y",pos=4,cex=3)y=c(2,3)x=c(2,1)cc = crossprod(x,y)/crossprod(x)segments(x*cc,x*cc,y,y,lty=2)text(x*cc,x*cc,expression(hat(Y)),pos=4,cex=3)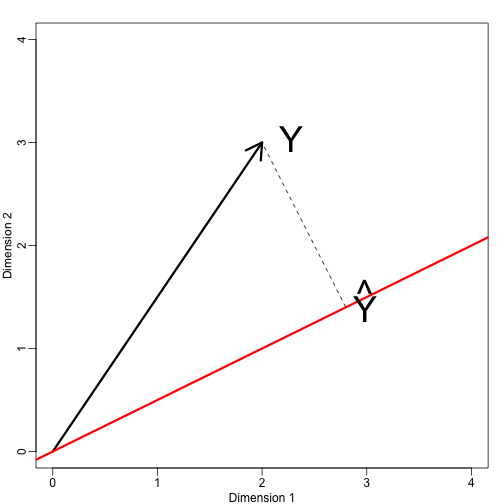
Megjegyezzük, hogy ha volt olyan, hogy , akkor egyszerűen és a tér nem változik. Ez az egyszerűsítés az egyik ok, amiért szeretjük az ortogonális mátrixokat.
Példa: A mintaátlag egy vetület
Legyen és az által átfogott tér:
Ebben a térben a vektorok minden összetevője azonos számú, így úgy gondolhatunk erre a térre, mint ami az állandókat képviseli: a vetületben minden dimenzió azonos értékű lesz. Mi minimalizálja tehát az és közötti távolságot?
Az ilyen problémákról beszélve néha kétdimenziós ábrákat használunk, mint például a fenti. Egyszerűen elvonatkoztatunk, és úgy gondolunk egy pontra az és-ben, mint egy kisebb számú, ebben az esetben csak egy érték által meghatározott altérre: .
A kérdésünkre visszatérve tudjuk, hogy a vetület:
amely ebben az esetben az átlag:
Ez esetben ugyanilyen egyszerű lett volna számtant is használni:
Példa: A regresszió is egy vetület
Adjunk egy kicsit bonyolultabb példát. Az egyszerű lineáris regresszió is magyarázható vetületekkel. Adataink (a továbbiakban nem fogjuk használni a jelölést) ismét egy vektor, a modellünk pedig egy egyenessel jósol . We want to find the and that minimize the distance between and the space defined by:
with:
Our matrix is and any point in can be written as .
The equation for the multidimensional version of orthogonal projection is:
which we have seen before and gives us:
And the projection to is therefore: