Nella nostra discussione sull’intervallo di confidenza per \(\mu_{Y}}), abbiamo usato la formula per studiare quali fattori influenzano la larghezza dell’intervallo di confidenza. Non c’è bisogno di farlo di nuovo. Poiché le formule sono così simili, si scopre che i fattori che influenzano l’ampiezza dell’intervallo di predizione sono identici ai fattori che influenzano l’ampiezza dell’intervallo di confidenza.
Indaghiamo invece la formula per l’intervallo di predizione per \(y_{new}}:
(\hat{y}_h \pm t_{(1-\alpha/2, n-2)} \tempi \sqrt{MSE \tempi \sinistra( 1+dfrac{1}{n} + \dfrac{(x_h-\bar{x})^2}{\sum(x_i-\bar{x})^2}\destra)
per vedere come si confronta con la formula dell’intervallo di confidenza per \(\mu_{Y}\):
(\hat{y}_h \pm t_{(1-\alfa/2, n-2)} \tempi \sqrt{MSE \sinistra(\dfrac{1}{n} + \dfrac{(x_h-\bar{x})^2}{\sum(x_i-\bar{x})^2}\destra)})
Osserva che l’unica differenza nelle formule è che l’errore standard della predizione per \(y_{new}\ ha un termine MSE extra in esso che l’errore standard del fit per \(\mu_{Y}\) non ha.
Cerchiamo di capire l’intervallo di predizione per vedere cosa causa il termine MSE extra. Nel farlo, iniziamo prima con un problema più semplice. Pensate a come potremmo predire una nuova risposta \(y_new}\ ad un particolare \(x_{h}\ se la media delle risposte \(\mu_{Y}\ a \(x_{h}\ fosse nota. Cioè, supponiamo che sia noto che la mortalità media per cancro della pelle a \(x_{h} = 40^{o}) N è di 150 morti per milione (con varianza 400)? Qual è la mortalità prevista per il cancro alla pelle a Columbus, Ohio?
Poiché \mu_{Y} = 150 \) e \(\sigma^{2} = 400 \) sono noti, possiamo sfruttare la “regola empirica”, che afferma tra l’altro che il 95% delle misure dei dati normalmente distribuiti sono entro 2 deviazioni standard della media. Cioè, dice che il 95% delle misure sono nell’intervallo compreso tra:
(\mu_{Y}- 2\sigma\) e \(\mu_{Y}+ 2\sigma\).
Applicando la regola del 95% al nostro esempio con \(\mu_{Y} = 150\) e \(\sigma= 20\):
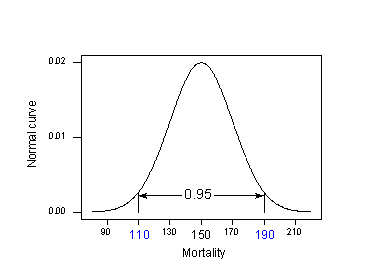
95% dei tassi di mortalità per cancro della pelle delle località a 40 gradi di latitudine nord sono nell’intervallo tra:
150 – 2(20) = 110 e 150 + 2(20) = 190.
Ovvero, se qualcuno volesse conoscere il tasso di mortalità per cancro della pelle per una località a 40 gradi nord, la nostra migliore ipotesi sarebbe tra 110 e 190 morti su 10 milioni. Il problema è che il nostro calcolo ha usato \(\mu_{Y}}) e \(\sigma\), valori di popolazione che tipicamente non conosciamo. La realtà si impone:
- La media \(\mu_{Y}}) non è tipicamente nota. La cosa più logica da fare è stimarla con la risposta prevista \(\mu_{y}}). Il costo dell’uso di \hat{y} per stimare \mu_{Y} è la varianza di \hat{y}. Cioè, diversi campioni produrrebbero diverse previsioni \(\hat{y}}), e quindi dobbiamo tenere conto di questa varianza di \(\hat{y}}).
- La varianza \(\sigma^{2}) non è tipicamente nota. La cosa più logica da fare è stimarla con l’MSE.
Perché dobbiamo stimare queste quantità sconosciute, la variazione nella previsione di una nuova risposta dipende da due componenti:
- la variazione dovuta alla stima della media \(\mu_{Y}}) con \hat{y}_h\, che denotiamo “\(\sigma^2(\hat{Y}_h)\).”(Si noti che la stima di questa quantità è solo il quadrato dell’errore standard dell’adattamento che appare nella formula dell’intervallo di confidenza.)
- la variazione nelle risposte y, che denotiamo come “\(\sigma^2\).”(Si noti che la quantità è stimata, come al solito, con l’errore quadratico medio MSE.)
Aggiungendo le due componenti della varianza, otteniamo:
(\sigma^2+ \sigma^2(\hat{Y}_h)\)
che è stimato da:
(MSE+MSE \left( \dfrac{1}{n} + \dfrac{(x_h-\bar{x})^2}{\sum_{i=1}^{n}(x_i-\bar{x})^2} \destra) =MSE\sinistra( 1+\dfrac{1}{n} + \dfrac{(x_h-\bar{x})^2}{\sum_{i=1}^{n}(x_i-\bar{x})^2}
Riconosci questa quantità? E’ solo la varianza della predizione che appare nella formula dell’intervallo di predizione \(y_{new}\)!
Confrontiamo di nuovo i due intervalli:
Intervallo di confidenza per \(\mu_{Y}\colon \hat{y}_h \pm t_{(1-\alpha/2, n-2)} \volte \sqrt{MSE \tempi \sinistra( \frac{1}{n} + \frac{(x_h-\bar{x})^2}{somma(x_i-\bar{x})^2}}destra)})
Intervallo di previsione per \(y_{new}\colon \hat{y}_h \pm t_{(1-\alfa/2, n-2)} \volte \sqrt{MSE \sinistra( 1+frac{1}{n}
Quali sono le implicazioni pratiche della differenza tra le due formule?
- Perché l’intervallo di predizione ha il termine MSE extra, un intervallo di confidenza per \mu_{Y} a \(x_h}) sarà sempre più stretto del corrispondente intervallo di predizione per \(y_new}) a \(x_h}).
- Calcolando l’intervallo alla media del campione dei valori del predittore \(\left(x_{h} = \bar{x}\right)\) e aumentando la dimensione del campione n, l’errore standard dell’intervallo di confidenza può avvicinarsi a 0. Poiché l’intervallo di predizione ha il termine extra MSE, l’errore standard dell’intervallo di predizione non può avvicinarsi a 0.
La prima implicazione si vede più facilmente studiando il seguente grafico per il nostro esempio di mortalità da cancro della pelle:
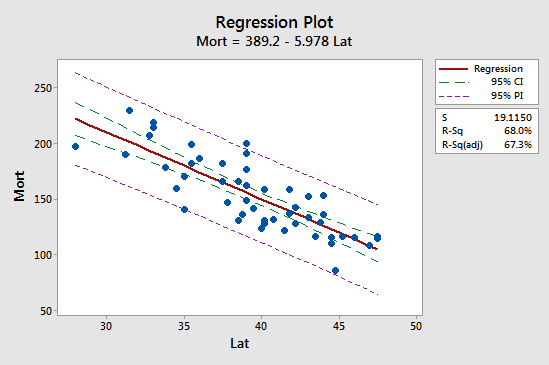
Osserva che l’intervallo di previsione (95% PI, in viola) è sempre più ampio dell’intervallo di confidenza (95% CI, in verde). Inoltre, entrambi gli intervalli sono più stretti alla media dei valori predittivi (circa 39,5).