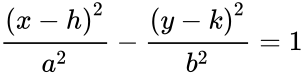Asse semimaggiore | Space Wiki

File:Asse semimaggiore.png

Il semiasse maggiore di un’ellisse

In geometria, il termine semiasse maggiore (anche asse semimaggiore) è usato per descrivere le dimensioni di ellissi e iperboli.

Elisse
Hyperbola
Astronomy
Orbital period
Distanza media
Energia; calcolo del semiasse maggiore dai vettori di stato
Esempio

Elisse

L’asse maggiore di un’ellisse è il suo diametro più lungo, una linea che passa per il centro ed entrambi i fuochi, le cui estremità sono nei punti più larghi della forma. Il semiasse maggiore è la metà dell’asse maggiore, e quindi va dal centro, attraverso un fuoco, fino al bordo dell’ellisse.

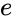
E’ legato al semiasse minore ${{displaystyle b\\code(TM)}$ attraverso l’eccentricità ${displaystyle e\code(TM)}$ e il semiasse maggiore.e il semi-lato retto ${{displaystyle \ell \\\,\\!$ , come segue:

${displaystyle b=a{sqrt {1-e^{2}}},\\!}$ ${displaystyle \ell =a(1-e^{2})\,\!}$ ${{displaystyle a\ell =b^{2},\!}$ .

Una parabola può essere ottenuta come il limite di una sequenza di ellissi in cui un fuoco è mantenuto fisso mentre l’altro è permesso di muoversi arbitrariamente lontano in una direzione, mantenendo ${displaystyle ell \\\,\!}$ fisso. Così ${{displaystyle a\,\\!}$ e ${displaystyle b\,\!}$ tendono all’infinito, ${displaystyle a\,\!$ più velocemente di ${{displaystyle b\\,\!}$ .

Il semiasse maggiore è il valore medio delle distanze più piccole e più grandi da un fuoco ai punti dell’ellisse. Consideriamo ora l’equazione in coordinate polari, con un fuoco nell’origine e l’altro sull’asse x positivo,

${{displaystyle r(1-e\cos \theta )=l\,\!}$

The mean value of $r={\ell \over {1+e}}\,\!$ and $r={\ell \over {1-e}}\,\!$ , is $a={\ell \over {1-e^{2}}}\,\!$ .

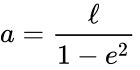
Hyperbola

The semi-major axis of a hyperbola is one half of the distance between the two branches; if this is a in the x-direction the equation is:

${\frac {\left(x-h\right)^{2}}{a^{2}}}-{\frac {\left(y-k\right)^{2}}{b^{2}}}=1$

In terms of the semi-latus rectum and the eccentricity we have

$a={\ell \over e^{2}-1}$

Astronomy

Orbital period

In astrodynamics the orbital period 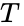$T\,$ of a small body orbiting a central body in a circular or elliptical orbit is:

$T=2\pi {\sqrt {a^{3}/\mu }}$

where:

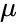
${displaystyle a\\,}$ è la lunghezza del semiasse maggiore dell’orbita ${displaystyle \mu }$ è il parametro gravitazionale standard

Nota che per tutte le ellissi con un dato semiasse maggiore, il periodo orbitale è lo stesso, indipendentemente dall’eccentricità.

In astronomia, il semiasse maggiore è uno degli elementi orbitali più importanti di un’orbita, insieme al suo periodo orbitale. Per gli oggetti del sistema solare, il semiasse maggiore è legato al periodo dell’orbita dalla terza legge di Keplero (originariamente derivata empiricamente),

${displaystyle T^{2}=a^{3},}$

dove T è il periodo in anni, e a è il semiasse maggiore in unità astronomiche. Questa forma risulta essere una semplificazione della forma generale per il problema dei due corpi, come determinato da Newton:

${displaystyle T^{2}={frac {4\pi ^{2}}{G(M+m)}}a^{3},}$

dove G è la costante gravitazionale, e M è la massa del corpo centrale, e m è la massa del corpo orbitante. Tipicamente, la massa del corpo centrale è talmente maggiore di quella del corpo orbitante, che m può essere ignorata. Facendo questa assunzione e usando le unità tipiche dell’astronomia si ottiene la forma più semplice che Keplero ha scoperto.

Sorprendentemente, il percorso del corpo orbitante intorno al baricentro e il suo percorso rispetto al suo primario sono entrambi ellissi. Il semiasse maggiore usato in astronomia è sempre la distanza primaria-secondaria; così, i parametri orbitali dei pianeti sono dati in termini eliocentrici. La differenza tra le orbite primocentriche e “assolute” può essere meglio illustrata guardando il sistema Terra-Luna. Il rapporto di massa in questo caso è 81,30059. La distanza caratteristica Terra-Luna, il semi-asse maggiore dell’orbita lunare geocentrica, è di 384.400 km. L’orbita lunare baricentrica, invece, ha un semiasse maggiore di 379.700 km, la differenza è data dalla contro-orbita terrestre, 4.700 km. La velocità orbitale baricentrica media della Luna è di 1,010 km/s, mentre quella della Terra è di 0,012 km/s. Il totale di queste velocità dà la velocità orbitale media geocentrica lunare, 1,022 km/s; lo stesso valore può essere ottenuto considerando solo il valore del semiasse maggiore geocentrico.

Distanza media

Si dice spesso che il semiasse maggiore è la distanza “media” tra il primario (il centro dell’ellisse) e il corpo orbitante. Questo non è del tutto esatto, in quanto dipende da cosa viene presa la media.

facendo la media della distanza sull’anomalia eccentrica (q.v.) si ottiene infatti il semiasse maggiore.
facendo la media sulla vera anomalia (il vero angolo orbitale, misurato al centro) si ottiene, stranamente, il semiasse minore ${{displaystyle b=a{sqrt {1-e^{2}}},\!$ .
facendo la media sull’anomalia media (la frazione del periodo orbitale che è trascorsa dal pericentro, espressa come angolo), infine, si ottiene la media temporale (che è ciò che “media” significa di solito per i profani): ${{displaystyle a(1+{frac {e^{2}}{2}})\,\\!}$ .

La media temporale dell’inverso del raggio, ${displaystyle r^{-1}},$ ${displaystyle a^{-1},$ .

Energia; calcolo del semiasse maggiore dai vettori di stato

In astrodinamica il semiasse maggiore ${displaystyle a\\,}$ può essere calcolato dai vettori di stato orbitale:

$a={-\mu \over {2\epsilon }}\,$ for an elliptical orbit and $a={\mu \over {2\epsilon }}\,$ for a hyperbolic trajectory

and

$\epsilon ={v^{2} \over {2}}-{\mu \over \left|\mathbf {r} \right|}$ (specific orbital energy)

and

$\mu =GM\,$ (standard gravitational parameter),

where:

$v\,$ is orbital velocity from velocity vector of an orbiting object,
$\mathbf {r} \,$ is cartesian position vector of an orbiting object in coordinates of a reference frame with respect to which the elements of the orbit are to be calculated (e.g. geocentrica equatoriale per un’orbita intorno alla Terra, o eclittica eliocentrica per un’orbita intorno al Sole),
${displaystyle G\,}$ è la costante gravitazionale,
${displaystyle M\,}$ la massa del corpo centrale.

Nota che per un dato corpo centrale e una data energia specifica totale, il semi-asse maggiore è sempre lo stesso, indipendentemente dall’eccentricità. Al contrario, per un dato corpo centrale e un dato semi-asse maggiore, l’energia specifica totale è sempre la stessa.

Esempio

La Stazione Spaziale Internazionale ha un periodo orbitale di 91,74 minuti, quindi il semi-asse maggiore è 6738 km . Ogni minuto in più corrisponde a circa 50 km in più: i 300 km in più di lunghezza dell’orbita richiedono 40 secondi, la velocità inferiore conta per altri 20 secondi.