In questa sezione, impareremo come trovare la radice (o le radici) di un’equazione quadratica. Le radici sono anche chiamate intercette x o zeri. Una funzione quadratica è rappresentata graficamente da una parabola con il vertice situato nell’origine, sotto l’asse x o sopra l’asse x. Pertanto, una funzione quadratica può avere una, due o zero radici.
Quando ci viene chiesto di risolvere un’equazione quadratica, in realtà ci viene chiesto di trovare le radici. Abbiamo già visto che il completamento del quadrato è un metodo utile per risolvere le equazioni quadratiche. Questo metodo può essere usato per ricavare la formula quadratica, che viene usata per risolvere le equazioni quadratiche. Infatti, le radici della funzione
f (x) = ax2 + bx + c
sono date dalla formula quadratica. Le radici di una funzione sono le intercette x. Per definizione, la coordinata y dei punti che giacciono sull’asse x è zero. Quindi, per trovare le radici di una funzione quadratica, poniamo f (x) = 0, e risolviamo l’equazione,
ax2 + bx + c = 0.
We can do this by completing the square as,
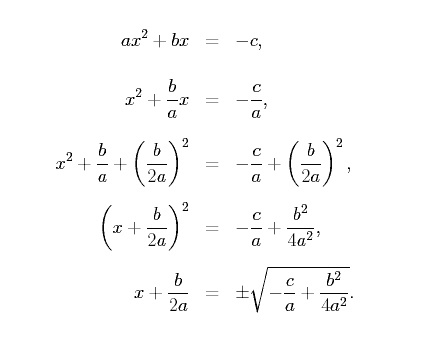
Solving for x and simplifying we have,
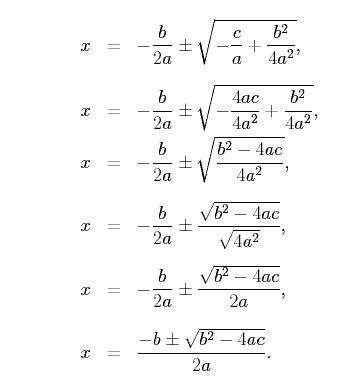
Thus, the roots of a quadratic function are given by,
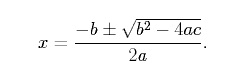
This formula is called the quadratic formula, and its derivation is included so that you can see where it comes from. We call the term b2 −4ac the discriminant. The discriminant is important because it tells you how many roots a quadratic function has. Specifically, if
1. b2 −4ac < 0 There are no real roots.
2. b2 −4ac = 0 There is one real root.
3. b2 −4ac > 0 There are two real roots.
We will examine each case individually.
Caso 1: Nessuna radice reale
Se il discriminante di una funzione quadratica è minore di zero, quella funzione non ha radici reali, e la parabola che rappresenta non interseca l’asse delle x. Poiché la formula quadratica richiede di prendere la radice quadrata del discriminante, un discriminante negativo crea un problema perché la radice quadrata di un numero negativo non è definita sulla linea reale. Un esempio di funzione quadratica senza radici reali è dato da,
f(x) = x2 – 3x + 4.
Notare che il discriminante di f(x) è negativo,
b2 -4ac = (-3)2- 4 – 1 – 4 = 9 – 16 = -7.
Questa funzione è rappresentata graficamente da una parabola che si apre verso l’alto il cui vertice si trova sopra l’asse x. Quindi il grafico non può mai intersecare l’asse x e non ha radici, come mostrato qui sotto,
Caso 2: Una radice reale
Se il discriminante di una funzione quadratica è uguale a zero, quella funzione ha esattamente una radice reale e incrocia l’asse x in un solo punto. Per vedere questo, impostiamo b2 -4ac = 0 nella formula quadratica per ottenere,
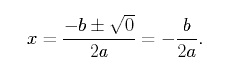
Si noti che 
è la coordinata x del vertice di una parabola. Così, una parabola ha esattamente una radice reale quando il vertice della parabola si trova proprio sull’asse x. L’esempio più semplice di una funzione quadratica che ha una sola radice reale è,
y = x2,
dove la radice reale è x = 0.
Un altro esempio di funzione quadratica con una radice reale è dato da,
f(x) = -4×2 + 12x – 9.
Si noti che il discriminante di f(x) è zero,
b2 -4ac = (12)2- 4 – -4 -9 = 144 – 144 = 0.
Questa funzione è rappresentata graficamente da una parabola che si apre verso il basso e ha vertice (3/2, 0), che giace sull’asse delle x. Thus, the graph intersects the x-axis at exactly one point (i.e. has one root) as shown below,
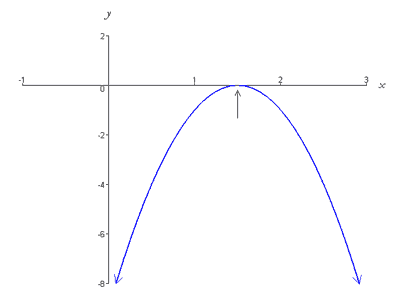
Case 3: Two Real Roots
If the discriminant of a quadratic function is greater than zero, that function has two real roots (x-intercepts). Taking the square root of a positive real number is well defined, and the two roots are given by,
An example of a quadratic function with two real roots is given by,
f(x) = 2×2− 11x + 5.
Notice that the discriminant of f(x) is greater than zero,