MO-teori och konjugerade pi-bindningar
Fördelen med att använda MO-teori för att förstå bindningar i organiska molekyler blir tydligare när vi tänker på pi-bindningar. Låt oss först betrakta pi-bindningen i eten ur en MO-teoretisk synvinkel (i det här exemplet kommer vi att bortse från s-bindningarna i molekylen och bara tänka på π-bindningen). Vi börjar med två atomorbitaler: en ohybridiserad 2p-orbital från varje kol. Var och en innehåller en enda elektron. I MO-teorin kombineras de två atomära matematiskt för att bilda två pi-molekylära orbitaler, en pi-bindningsorbital med låg energi och en pi*-antibindningsorbital med hög energi.

Molekylära orbitaler för eten (eten)
I den bindande pi-orbitalen interagerar de två skuggade loberna i p-orbitalerna konstruktivt med varandra, liksom de två oskuggade loberna (kom ihåg att det godtyckliga valet av skuggning representerar matematiska (+) och (-)-tecken för den matematiska vågfunktion som beskriver orbitalet). Det finns en ökad elektrontäthet mellan de två kolkärnorna i molekylorbitalet – det är en bindningsinteraktion.
I den högre energirelaterade antibindande pi*-orbitalet interagerar den skuggade loben i den ena p-orbitalet destruktivt med den oskuggade loben i den andra p-orbitalet, vilket leder till en knut mellan de två atomkärnorna och en övergripande repulsion mellan kolkärnorna.
Också med hjälp av ”uppbyggnadsprincipen” placerar vi de två elektronerna i den molekylära pi-orbitalen med lägre energi och bindning. Den antibindande pi*-orbitalen förblir tom.
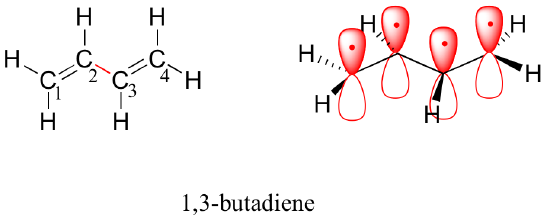
Nästan ska vi betrakta 1,3-butadienmolekylen. Enbart utifrån teorin om valensorbitaler skulle vi kunna förvänta oss att C2-C3-bindningen i denna molekyl, eftersom den är en sigma-bindning, skulle kunna rotera fritt.

Experimentellt observeras dock att det finns en betydande barriär för rotation kring C2-C3-bindningen, och att hela molekylen är planär. Dessutom är C2-C3-bindningen 148 pm lång, vilket är kortare än en typisk kol-kol enkelbindning (ca 154 pm), men längre än en typisk dubbelbindning (ca 134 pm).
Molekylärorbitalteori förklarar dessa observationer med begreppet delokaliserade pi-bindningar. I denna bild kombineras de fyra 2p-atomorbitalerna matematiskt för att bilda fyra pi-molekylorbitaler med ökande energi. Två av dessa – de bindande pi-orbitalerna – har lägre energi än de p-atomorbitaler från vilka de bildas, medan två – de antibindande pi*-orbitalerna – har högre energi.

Den molekylära orbital som har den lägsta energin, pi1, har endast konstruktiva växelverkningar och noll noder. Högre i energi, men fortfarande lägre än de isolerade p-orbitalerna, har orbital pi2 en nod men två konstruktiva interaktioner – det är alltså fortfarande en bindande orbital totalt sett. Om man tittar på de två antibindande orbitalerna har pi3* två noder och en konstruktiv växelverkan, medan pi4* har tre noder och noll konstruktiva växelverkningar.
Enligt aufbau-principen placeras de fyra elektronerna från de isolerade 2pz-atomorbitalerna i de bindande pi1- och pi2-obbitalerna. Eftersom pi1 innefattar konstruktiv växelverkan mellan C2 och C3 finns det i 1,3-butadienmolekylen en viss grad av pi-bindande växelverkan mellan dessa två kolväten, vilket förklarar dess kortare längd och barriär för rotation. Bilden av valensbindningen av 1,3-butadien visar att de två pi-bindningarna är isolerade från varandra, med varje par pi-elektroner ”fast” i sin egen pi-bindning. Molekylorbitalteorin förutsäger dock (korrekt) att de fyra pi-elektronerna i viss utsträckning är delokaliserade, eller ”utspridda”, över hela pi-systemet.
Rymdfyllnadsvy
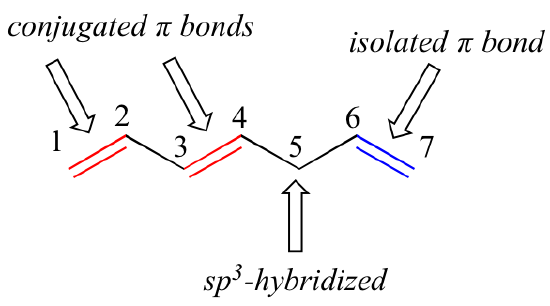
1,3-butadien är det enklaste exemplet på ett system av konjugerade pi-bindningar. För att betraktas som konjugerade måste två eller flera pi-bindningar separeras av endast en enkel bindning – med andra ord kan det inte finnas ett mellanliggande sp3-hybridiserat kol, eftersom detta skulle bryta upp det överlappande systemet av parallella p-orbitaler. I föreningen nedan är till exempel dubbelbindningarna C1-C2 och C3-C4 konjugerade, medan dubbelbindningen C6-C7 är isolerad från de andra två pi-bindningarna genom den sp3-hybridiserade C5.
Ett mycket viktigt begrepp att ha i åtanke är att det finns en inneboende termodynamisk stabilitet förknippad med konjugering. Denna stabilitet kan mätas experimentellt genom att jämföra hydreringsvärmen för två olika diener. (Hydrogenering är en reaktionstyp som vi kommer att lära oss mycket mer om i kapitel 15: i huvudsak är det processen att lägga till en vätemolekyl – två protoner och två elektroner – till en p-bindning). När de två konjugerade dubbelbindningarna i 1,3-pentadien ”hydreras” för att producera pentan frigörs cirka 225 kJ per mol pentan som bildas. Jämför det med de cirka 250 kJ/mol som frigörs när de två isolerade dubbelbindningarna i 1,4-pentadien hydreras, vilket också bildar pentan.
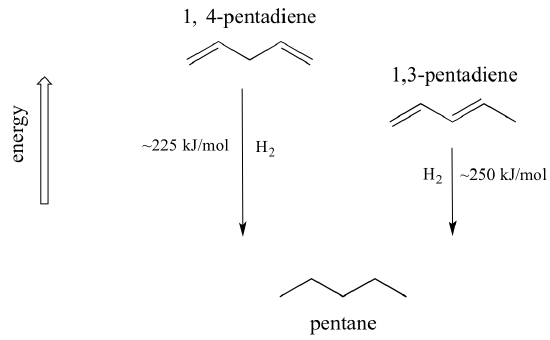
Den konjugerade dienen har lägre energi: den är med andra ord mer stabil. I allmänhet är konjugerade pi-bindningar stabilare än isolerade pi-bindningar.
Konjugerade pi-system kan innefatta syre- och kväveatomer samt kol. I fettmolekylers ämnesomsättning involverar några av nyckelreaktionerna alkener som är konjugerade till karbonylgrupper.

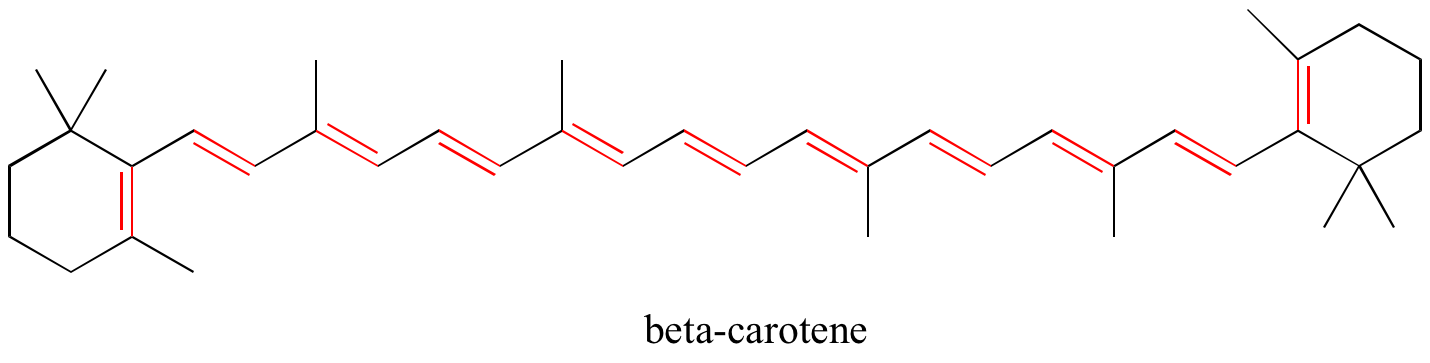
I kapitel 4 kommer vi att se att MO-teorin är mycket användbar när det gäller att förklara varför organiska molekyler som innehåller utökade system av konjugerade pi-bindningar ofta har distinkta färger. Betakaroten, den förening som är ansvarig för morötternas orange färg, har ett utvidgat system med 11 konjugerade pi-bindningar.
Övning: Identifiera alla konjugerade och isolerade dubbelbindningar i strukturerna nedan. För varje konjugerat pi-system, ange antalet överlappande p-orbitaler och hur många pi-elektroner som delas mellan dem.
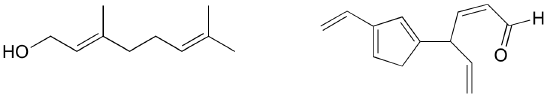
Övning: Identifiera alla isolerade och konjugerade pi-bindningar i lykopen, den rödfärgade föreningen i tomater. Hur många pi-elektroner ingår i det konjugerade pi-systemet?

Lösningar till övningar
Aromatik – det ultimata konjugerade systemet
Molekylärorbitalteori är särskilt användbar när det gäller att förklara de unika egenskaperna hos aromatiska föreningar som bensen:
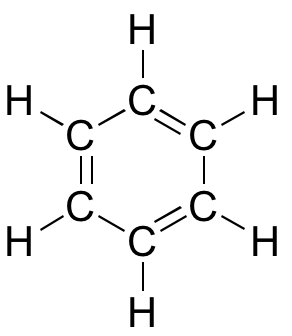
3D interaktiv modell av bensen
Och även om bensen oftast ritas med tre dubbelbindningar och tre enkelbindningar är i själva verket alla kol-kol-bindningar exakt lika långa (138 pm). Dessutom är pi-bindningarna i bensen betydligt mindre reaktiva än ”normala” pi-bindningar, antingen isolerade eller konjugerade. Något i bensenens struktur gör att dess pi-bindningar är särskilt stabila. Detta ”något” har ett namn: det kallas ”aromaticitet”.
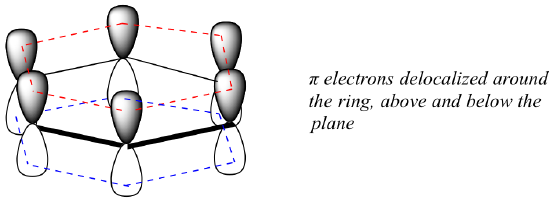
Vad exakt är denna ”aromatiska” egenskap som gör pi-bindningarna i bensen så stabila? Till stor del ligger svaret på denna fråga i det faktum att bensen är en cyklisk molekyl där alla ringatomer är sp2-hybridiserade. Detta gör det möjligt för pi-elektronerna att vara delokaliserade i molekylära orbitaler som sträcker sig hela vägen runt ringen, över och under planet. För att detta ska kunna ske måste naturligtvis ringen vara plan – annars skulle p-orbitalerna inte kunna överlappa varandra ordentligt. Bensen är faktiskt känd för att vara en plan molekyl.
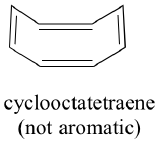
Har alla cykliska molekyler med omväxlande enkel- och dubbelbindningar samma aromatiska stabilitet? Svaret är faktiskt nej. Den åttadelade cyklooktatetraenringen som visas nedan är inte platt, och dess π-bindningar reagerar som ”normala” alkener.
Det krävs uppenbarligen något mer för att den ska vara aromatisk, och detta kan bäst förklaras med molekylär orbitalteori. Låt oss titta på ett energidiagram över pi-molekylorbitalerna i bensen.
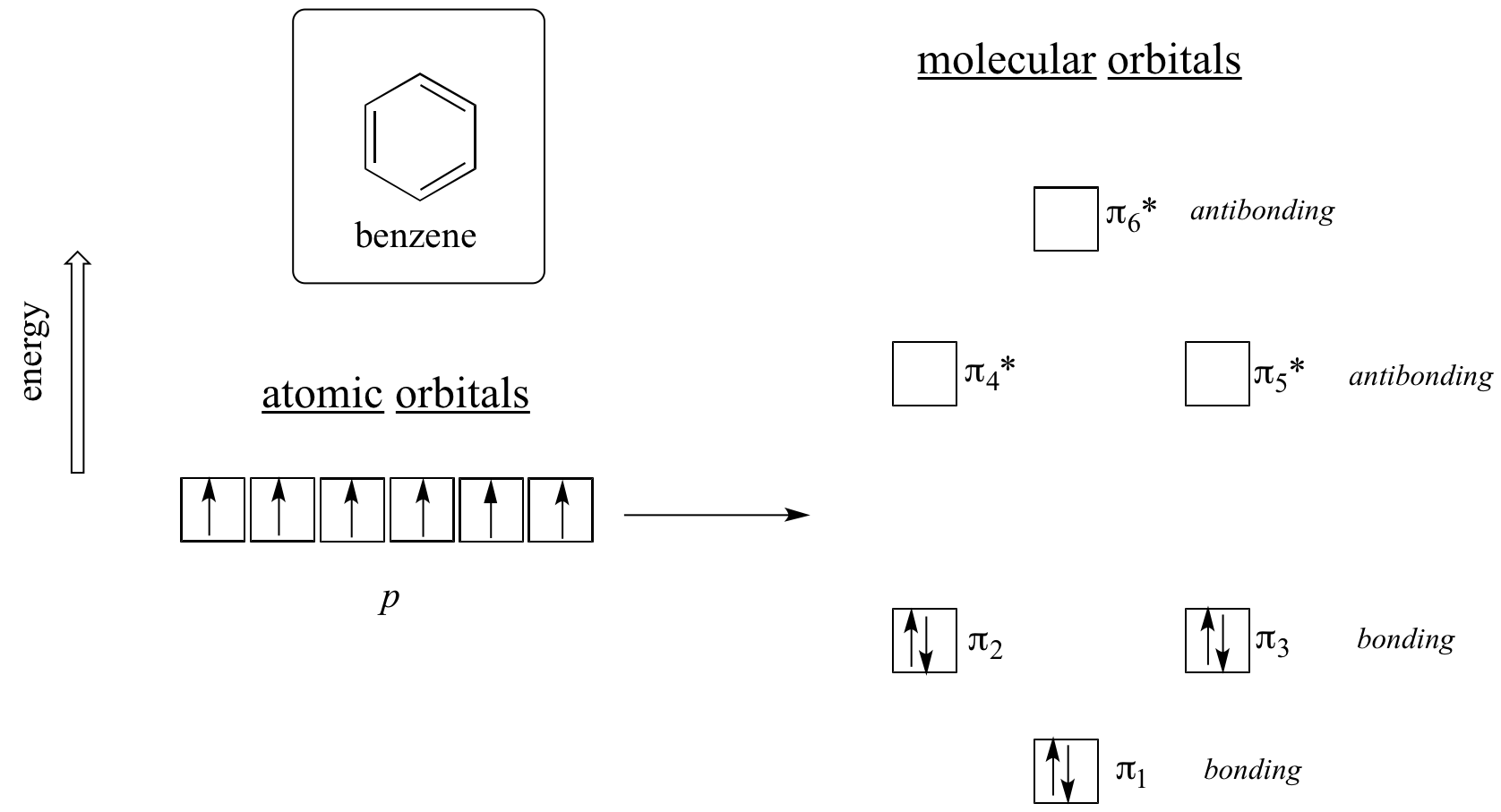
Kvantmekaniska beräkningar talar om för oss att de sex pi-molekylorbitalerna i bensen, som bildas av sex atomära p-orbitaler, upptar fyra separata energinivåer. Pi1 och pi6* har unika energinivåer, medan paren pi2 – pi3 och pi4* – pi5* är degenererade, vilket innebär att de befinner sig på samma energinivå. När vi använder aufbau-principen för att fylla dessa orbitaler med de sex pi-elektronerna i bensen ser vi att de bindande orbitalerna är helt fyllda och att de antibindande orbitalerna är tomma. Detta ger oss en bra ledtråd till källan till bensenens speciella stabilitet: en full uppsättning bindnings-MO:s liknar på många sätt det ”fulla skalet” av elektroner i atomorbitalerna hos de stabila ädelgaserna helium, neon och argon.
Nu gör vi samma sak för cyklooktatetraen, som vi redan har lärt oss att det inte är aromatiskt.
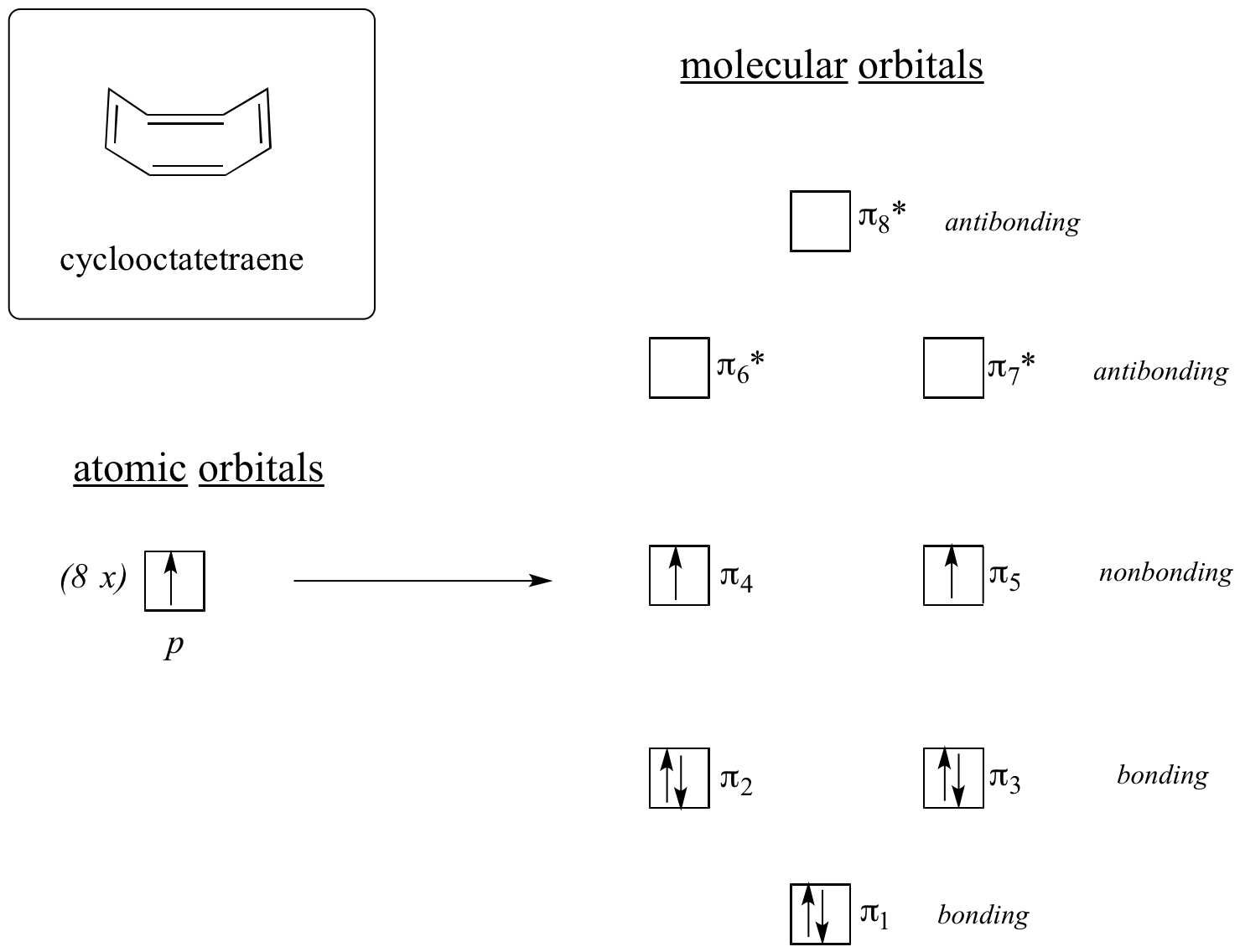
Resultatet av beräkningar av molekylära orbitaler talar om för oss att de MO med lägst och högst energi (pi1 och pi8*) har unika energinivåer, medan de övriga sex bildar degenererade par. Lägg märke till att pi4 och pi5 ligger på samma energinivå som de isolerade 2pz-atomorbitalerna: dessa är därför varken bindande eller antibindande, utan kallas snarare icke-bindande MOs. Genom att fylla MOs med de åtta pi-elektronerna i molekylen finner vi att de sista två elektronerna är oparade och faller in i de två degenererade icke-bindande orbitaler. Eftersom vi inte har ett perfekt fyllt skal av bindande MOs är vår molekyl inte aromatisk. Följaktligen fungerar var och en av dubbelbindningarna i cyklooktatetraen mer som en isolerad dubbelbindning.
För tillfället är det viktiga inlärningsmålet att känna igen konjugerade pi-bindningssystem och förstå att bensen är exceptionellt stabilt och uppvisar en egenskap som kallas aromaticitet. Aromaticitet och kemin hos aromatiska föreningar är relativt komplex och diskuteras mer ingående i efterföljande kapitel i denna text.
Organic Chemistry With a Biological Emphasis av Tim Soderberg (University of Minnesota, Morris)