I vår diskussion om konfidensintervallet för \(\mu_{Y}\) använde vi formeln för att undersöka vilka faktorer som påverkar bredden på konfidensintervallet. Det finns ingen anledning att göra det igen. Eftersom formlerna är så lika visar det sig att de faktorer som påverkar prediktionsintervallets bredd är identiska med de faktorer som påverkar konfidensintervallets bredd.
Låt oss istället undersöka formeln för prediktionsintervallet för \(y_{new}\):
\(\hat{y}_h \pm t_{(1-\alpha/2, n-2)} \times \sqrt{MSE \times \left( 1+\dfrac{1}{n} + \dfrac{(x_h-\bar{x})^2}{\sum(x_i-\bar{x})^2}\right)}\)
för att se hur det går att jämföra med formeln för konfidensintervallet för \(\mu_{Y}\):
\(\hat{y}_h \pm t_{(1-\alpha/2, n-2)} \times \sqrt{MSE \left(\dfrac{1}{n} + \dfrac{(x_h-\bar{x})^2}{\sum(x_i-\bar{x})^2}\right)}\)
Observera att den enda skillnaden i formlerna är att standardfelet för förutsägelsen för \(y_{new}\) har en extra MSE-term i sig som standardfelet för anpassningen för \(\mu_{Y}\) inte har.
Låt oss försöka förstå prediktionsintervallet för att se vad som orsakar den extra MSE-termen. När vi gör det börjar vi med ett enklare problem först. Tänk på hur vi skulle kunna förutsäga ett nytt svar \(y_{new}\) vid en viss \(x_{h}\) om medelvärdet av svaren \(\mu_{Y}\) vid \(x_{h}\) var känt. Anta att man vet att den genomsnittliga dödligheten i hudcancer vid \(x_{h} = 40^{o}\) N är 150 dödsfall per miljon (med en varians på 400)? Vad är den förutspådda hudcancerdödligheten i Columbus, Ohio?
Då \(\mu_{Y} = 150 \) och \( \sigma^{2} = 400\) är kända kan vi dra nytta av den ”empiriska regeln”, som bland annat säger att 95 % av mätningarna av normalfördelade data ligger inom 2 standardavvikelser från medelvärdet. Den säger alltså att 95 % av mätningarna ligger i intervallet mellan:
\(\mu_{Y}- 2\sigma\) och \(\mu_{Y}+ 2\sigma\).
Användning av 95 %-regeln på vårt exempel med \(\mu_{Y} = 150\) och \(\sigma= 20\):
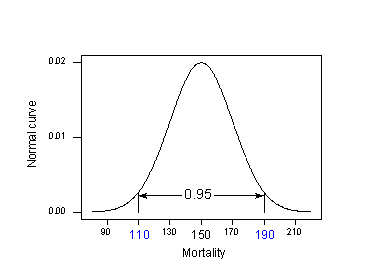
95 % av dödligheten i hudcancer på platser vid 40 graders nordlig latitud ligger i intervallet mellan:
150 – 2(20) = 110 och 150 + 2(20) = 190.
Det vill säga, om någon vill veta dödligheten i hudcancer för en plats på 40 grader nordlig bredd skulle vår bästa gissning vara någonstans mellan 110 och 190 dödsfall per 10 miljoner. Problemet är att vår beräkning använde \(\mu_{Y}\) och \(\sigma\), befolkningsvärden som vi vanligtvis inte känner till. Verkligheten sätter in:
- Medelvärdet \(\mu_{Y}\) är vanligtvis inte känt. Det logiska är att uppskatta den med hjälp av det förutspådda svaret \(\hat{y}\). Kostnaden för att använda \(\hat{y}\) för att uppskatta \(\mu_{Y}\) är variansen i \(\hat{y}\). Det vill säga, olika stickprov skulle ge olika förutsägelser \(\hat{y}\), och därför måste vi ta hänsyn till denna varians av \(\hat{y}\).
- Variansen \( \sigma^{2}\) är vanligtvis inte känd. Det logiska är att skatta den med MSE.
Eftersom vi måste skatta dessa okända storheter beror variationen i förutsägelsen av ett nytt svar på två komponenter:
- variationen på grund av att skatta medelvärdet \(\mu_{Y}\) med \(\hat{y}_h\) , som vi benämner ”\(\sigma^2(\hat{Y}_h)\)”.” (Observera att uppskattningen av denna kvantitet bara är kvadraten på standardfelet för anpassningen som visas i formeln för konfidensintervallet.)
- variationen i svaren y, som vi betecknar som ”\(\sigma^2\).” (Observera att kvantiteten skattas som vanligt med medelkvadratfelet MSE.)
Om vi adderar de två varianskomponenterna får vi:
\(\sigma^2+\sigma^2(\hat{Y}_h)\)
som skattas genom:
\(MSE+MSE \left( \dfrac{1}{n} + \dfrac{(x_h-\bar{x})^2}{\sum_{i=1}^{n}(x_i-\bar{x})^2} \right) =MSE\left( 1+\dfrac{1}{n} + \dfrac{(x_h-\bar{x})^2}{\sum_{i=1}^{n}(x_i-\bar{x})^2} \right) \)
Känner du igen denna kvantitet? Det är bara variansen för förutsägelsen som visas i formeln för förutsägelseintervallet \(y_{new}\)!
Låt oss jämföra de två intervallen igen:
Konfidensintervallet för \(\(\mu_{Y}\kolon \hat{y}_h \pm t_{(1-\alpha/2, n-2)} \times \sqrt{MSE \times \left( \frac{1}{n} + \frac{(x_h-\bar{x})^2}{\sum(x_i-\bar{x})^2}\right)}\)
Prediktionsintervall för \(y_{new}\colon \hat{y}_h \pm t_{(1-\alpha/2, n-2)} \times \sqrt{MSE \left( 1+\frac{1}{n} + \frac{(x_h-\bar{x})^2}{\sum(x_i-\bar{x})^2}\right)}\)
Vad innebär skillnaden mellan de två formlerna i praktiken?
- Eftersom prediktionsintervallet har den extra MSE-termen kommer ett \( \left( 1-\alpha \right) 100\% \) konfidensintervall för \(\mu_{Y}\) vid \(x_{h}\) alltid att vara smalare än motsvarande \( \left( 1-\alpha \right) 100\% \) prediktionsintervall för \(y_{new}\) vid \(x_{h}\).
- Om man beräknar intervallet vid provets medelvärde av prediktorvärdena \(\left(x_{h} = \bar{x}\right)\) och ökar provstorleken n, kan konfidensintervallets standardfel närma sig 0. Eftersom prediktionsintervallet har den extra MSE-termen kan prediktionsintervallets standardfel inte komma i närheten av 0.
Den första implikationen syns lättast genom att studera följande plot för vårt exempel på dödlighet i hudcancer:
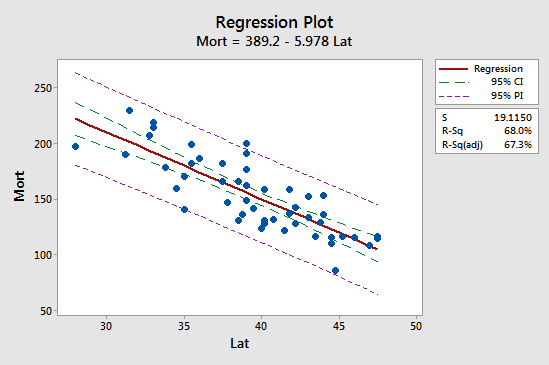
Observera att prediktionsintervallet (95 % PI, i lila) alltid är bredare än konfidensintervallet (95 % CI, i grönt). Dessutom är båda intervallen smalast vid medelvärdet av prediktionsvärdena (ca 39,5).