En Cobb-Douglas produktionsfunktion modellerar förhållandet mellan produktionsresultat och produktionsinsatser (faktorer). Den används för att beräkna förhållandet mellan insatsvaror för effektiv produktion och för att uppskatta tekniska förändringar i produktionsmetoder. Den allmänna formen för en Cobb-Douglas produktionsfunktion för en uppsättning \(n\) insatsvaror är\ där \(Y\) står för produktionen, \(x_{i}\) för insatsvaror \(i\) och \(\gamma\) och \(\alpha_{i}\) är parametrar som bestämmer produktionens totala effektivitet och produktionens reaktionsförmåga på förändringar i insatsvarornas kvantiteter. Tillämpningen av denna funktionella form för att mäta produktionen beror på matematikern Charles Cobb och ekonomen Paul Douglas, som använde den för att undersöka den relativa betydelsen av de två insatsfaktorerna arbete och kapital för tillverkningsindustrins produktion i USA under perioden 1899-1922. I sin ursprungliga modell begränsar Cobb och Douglas produktionselasticitetsparametrarna \(\alpha_{1}\) och \(\alpha_{2}\) till intervallet \(\alpha_{i}\in\left(0,1\right)\) och till att summera till ett, vilket innebär konstant skalavkastning. Funktionen är således\ där \(x_{1}\) och \(x_{2}\) står för arbete respektive kapital. Genom att ta den naturliga logaritmen av båda sidorna av ekvationen fås\ så att parametrarna \(\gamma\) och \(\alpha_{1}\) för uppgifter om produktion, arbete och kapital kan uppskattas med hjälp av Ordinary Least Squares. På grundval av sina uppgifter finner Cobb och Douglas ett värde på 0,75 för \(\alpha_{1}\), vilket innebär att arbetskraften stod för tre fjärdedelar av värdet av den amerikanska tillverkningsindustrins produktion (kapitalet stod för den resterande fjärdedelen) under den undersökta perioden. Deras uppskattning av effektivitetsparametern \(\gamma\) är 1,01, vilket, eftersom det är större än 1, återspeglar de positiva effekterna av icke observerbara krafter på produktionen genom kombinationen av arbete och kapital.
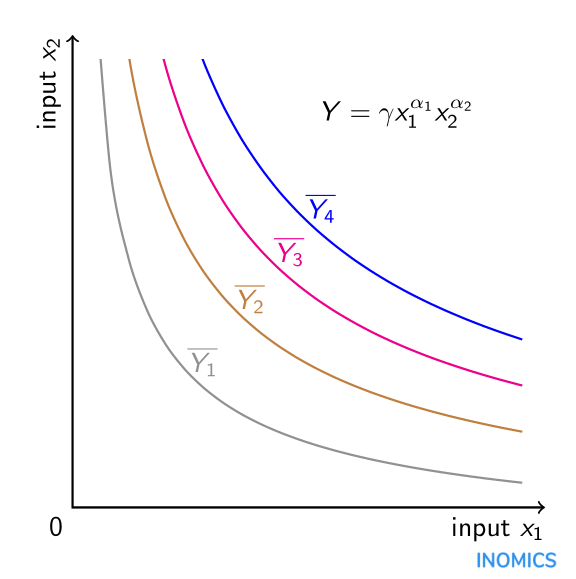
Den multiplikativa karaktären hos en Cobb-Douglas-produktionsfunktion, med positiva värden för \(\alpha_{i}\), innebär att insatsvarorna kompletterar varandra i produktionen. I standardmodellen för arbete och kapital ökar en ökning av kapitalmängden produktionen inte bara direkt, utan också indirekt genom dess inverkan på arbetets produktivitet. Matematiskt sett är den tvärpartiella derivatan av produktionsresultatet \(Y\) med avseende på arbete \(x_{1}\) och kapital \(x_{2}\) positiv. På grund av antagandet att \(\(\alpha_{i}\i\in\vänster(0,1\right)\) är dessutom den andra ordningens partiella derivat av produktionsresultatet med avseende på arbete och kapital båda negativa, vilket innebär minskande marginalavkastning för varje enskild insatsvara. Genom att helt enkelt lägga till antingen mer arbete eller mer kapital (men inte båda) i produktionsprocessen ökar produktionen, men i minskande takt. Substitutionselasticiteten mellan insatsvarorna är dessutom konstant och lika med ett på grund av den funktionella formen. En Cobb-Douglas-produktionsfunktion med två insatsvaror kan representeras grafiskt i form av isokvanter: kombinationer av båda insatsvarorna för vilka produktionen är konstant. Det finns fyra sådana isokvanter i grafen här för de (konstanta) produktionsnivåerna \(\overline{Y_{1}}}\), \(\overline{Y_{2}}}\), \(\(\overline{Y_{3}}}\) och \(\(\overline{Y_{4}}}\). Ju längre isokvant från ursprunget, desto större är produktionsnivån \(\(\overline{Y_{4}}}>\overline{Y_{3}}>\overline{Y_{2}}>\overline{Y_{1}}}\). Vilken exakt kombination av insatsvarorna \(x_{1}\) och \(x_{2}\) som är optimal för produktionen bestäms av den budget som producenten har till sitt förfogande samt kostnadsförhållandet mellan insatsvaran \(x_{2}\) och insatsvaran \(x_{1}\), vilket kan ingå i grafen i form av en isokostnadslinje (se artikeln om substitutionselasticitet).
Cobb och Douglas erkände själva att deras produktionsfunktion inte vilar på en solid teoretisk grund, och att den inte heller ska uppfattas som en produktionslag, utan endast utgör en statistisk approximation av de observerade sambanden mellan produktionsinsatser och produktion. Trots detta är dess enkla matematiska egenskaper attraktiva för ekonomer och har lett till att den har blivit en standard inom mikroekonomisk teori under det senaste århundradet.
Fortsatt läsning:
För bakgrunden och en översikt över de viktigaste egenskaperna hos Cobb-Douglas produktionsfunktioner, se framför allt avsnitten 6, 7 och 8 i Cobbs och Douglas ursprungliga artikel, ”A Theory of Production” (The American Economic Review, 1928).
Godt att veta:
Cobb-Douglas funktionella form används inte bara i produktionsteorin utan har också blivit standard i mikroekonomisk konsumentteori där den tillämpas som en nyttofunktion, där \(Y\) blir \(U\) för nyttan. \(x_{i}\) representerar då konsumtionsobjekt och när nyttofunktionen maximeras med en budgetrestriktion anger värdena för \(\alpha_{i}\) hur individen optimalt kommer att fördela budgeten mellan objekten.