
När man tänker på spioner och hemliga agenter kan man tänka på många saker: smarta prylar, utlandsresor, farliga missiler, snabba bilar och att bli skakad men inte rörd. Du skulle förmodligen inte tänka på matematik. Men det borde du göra.
Att knäcka koder och avslöja den sanna innebörden i hemliga meddelanden kräver massor av matematik, från enkel addition och subtraktion till datahantering och logiskt tänkande. Faktum är att några av de mest berömda kodknäckarna i historien har varit matematiker som har kunnat använda ganska enkel matematik för att avslöja komplotter, identifiera förrädare och påverka strider.
The Roman Geezer
Låt mig ge dig ett exempel. För nästan 2000 år sedan var Julius Caesar upptagen med att ta över världen och invadera länder för att öka romarrikets storlek. Han behövde ett sätt att kommunicera sina stridsplaner och taktik till alla på hans sida utan att fienden fick reda på det. So Caesar would write messages to his generals in code. Instead of writing the letter ’A’, he would write the letter thatcomes three places further on in the alphabet, the letter ’D’. Instead of a ’B’, he would write an ’E’, instead of a ’C’, he would write an ’F’ and so on. When he got to the end of the alphabet, however, he would have to go right back to the beginning, so instead of an ’X’, he would write an ’A’, instead of a ’Y’, he’d write a ’B’ and instead of ’Z’, he’d write a ’C’.
Complete the table to find out how Caesar would encode the following message:
| Caesar’s message | A | T | T | A | C | K | A | T | D | A | W | N | ||
| B | U | |||||||||||||
| C | V | |||||||||||||
| Coded message | D |
When Caesar’s generals came to decipher the messages, they knew that all they had to do was go back three places in the alphabet. Have a go at trying to work out these messages which could have been sent by Caesar or his generals:
hqhpb dssurdfklqj
wkluwb ghdg
uhwuhdw wr iruhvw
Easy as 1, 2, 3
This all seems very clever, but so far it’s all been letters and no numbers. So where’s the maths? The maths comes if you think of the letters as numbers from 0 to 25 with A being 0, B being 1, C being 2 etc. Then encoding, shifting the alphabet forward three places, is the same as adding three to your starting number:
| A | B | C | D | E | F | G | H | I | J | K | L | M | N | O | P | Q | R | S | T | U | V | W | X | Y | Z |
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 |
For example, encoding the letter ’A’ is 0+3=3, which is a ’D’.
Coding ’I’ is: 8+3=11, which is ’L’.
However, you do have to be careful when you get to the end of the alphabet, because there is no letter number 26, so you have to go back to number 0. In maths we call this ’MOD 26’, instead of writing 26, we go back to 0.
Have a go at coding your name by adding 3 to every letter. Then have a go at coding your name by shifting the alphabet forward by more places by adding greater numbers eg adding 5, then adding 10. Then have a go at decoding. Om bokstäverna är siffror och kodning är addition är avkodning subtraktion, så om du har kodat ett meddelande genom att lägga till 5 måste du avkoda meddelandet genom att subtrahera 5.
Rsak!
Om du har lärt dig att koda meddelanden genom att flytta alfabetet framåt har du kanske insett att det faktiskt är ganska enkelt att knäcka denna typ av kod. Det kan lätt göras bara genom försök och misstag. En fientlig kodknäckare skulle bara behöva prova 25 olika möjliga förskjutningar innan de kunde läsa dina meddelanden, vilket innebär att dina meddelanden inte skulle vara hemliga på mycket länge.
Så, vad sägs om att koda meddelanden på ett annat sätt? I stället för att skriva en bokstav skulle vi kunna skriva en symbol eller rita en bild. I stället för ett ”A” skulle vi kunna skriva *, i stället för ett ”B” skriva + osv. Länge trodde man att denna typ av kod skulle vara mycket svår att knäcka. Det skulle ta fienden alldeles för lång tid att räkna ut vilken bokstav i alfabetet varje symbol stod för bara genom att prova alla möjliga kombinationer av bokstäver och symboler. Det finns 400 miljoner miljarder miljarder miljarder möjliga kombinationer!
Denna typ av kod användes av Mary Queen of Scots när hon konspirerade mot Elizabeth den första. Mary ville döda Elizabeth så att hon själv kunde bli drottning av England och skickade kodade meddelanden av detta slag till sin medkonspiratör Anthony Babington. Tyvärr för Mary finns det ett mycket enkelt sätt att knäcka koden, som inte kräver försök och misstag, men som däremot, överraskande nog, kräver matematik.

Brev skickat av Mary Queen of Scots till sin medkonspiratör Anthony Babington. Varje symbol står för en bokstav i alfabetet.
Brev i ett språk är ganska ovanliga eftersom vissa används oftare än andra bokstäver. Ett enkelt experiment som du kan göra för att testa detta är att få alla i klassen att räcka upp handen om de har bokstaven ”E” i sitt namn. Låt sedan alla som har ett ”Z” räcka upp handen, sedan ett ”Q” och sedan ett ”A”. Du kommer förmodligen att upptäcka att ”E” och ”A” är vanligare än ”Z” och ”Q”. Grafen nedan visar den genomsnittliga frekvensen av bokstäver på engelska. För att sammanställa informationen har människor tittat igenom tusentals och åter tusentals böcker, tidskrifter och tidningar och räknat hur många gånger varje bokstav har dykt upp.
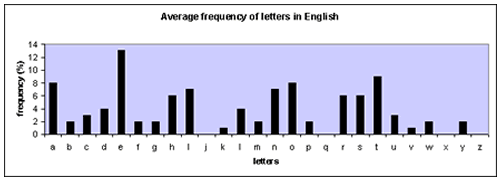
På engelska är E den vanligaste bokstaven. I varje skrift använder vi E ungefär 13 % av tiden i genomsnitt. ’T’ är den näst vanligaste bokstaven och ’A’ är den tredje vanligaste bokstaven.
Och det är denna information som kan hjälpa dig att knäcka koder. Allt Elisabet den förstas spionmästare behövde göra för att knäcka Marys kod var att titta igenom det kodade meddelandet och räkna hur många gånger varje symbol dök upp. Den symbol som dök upp flest gånger skulle förmodligen stå för bokstaven ”E”. Titta på vårt problem med forntida runor för en annan kod som kan dechiffreras genom att räkna hur ofta varje symbol dyker upp.
När man knäcker sådana här koder genom att leta efter den vanligaste bokstaven kallas det för ”frekvensanalys”, och det var denna smarta metod för att knäcka koder som resulterade i att Maria fick sitt huvud avhugget. CHOP!
Testa dina talanger
Att knäcka dessa kodade meddelanden innebär inte bara att leta efter den vanligaste symbolen, du kan också leta efter symboler som står helt ensamma i meddelandet, dvs. ord med en bokstav. Det finns bara två enbokstavsord på engelska, ”A” och ”I”, så en ensam symbol måste stå för ett ”A” eller ”I”. En annan sak du kan hålla utkik efter är vanliga ord. De vanligaste orden med tre bokstäver på engelska är ”the” och ”and”, så om du ser en grupp av tre symboler som dyker upp ganska ofta kan de stå för ”the” eller ”and”.
Om du vill testa dessa tips för att bryta koder och dina nya talanger för att bryta koder kan du ta en titt på Simon Singhs Black Chamber. Där finns Caesar shift- och frekvensanalyspussel som du kan knäcka och andra koder som du kan försöka lösa.
För mer information om andra hemliga koder som har använts genom historien kan du kolla in Simon Singhs webbplats. Den är full av information om alla sorters koder, inklusive den berömda historien Enigma, den kodmaskin som tyskarna använde under andra världskriget. Tyskarna trodde att deras kod var oövervinnerlig, men otroligt nog lyckades brittiska matematiker knäcka koden och läsa alla meddelanden som tyskarna skickade under kriget. Historiker tror att denna insiderinformation förkortade kriget med två hela år.
VARNING
När du har läst det här kanske du vill hitta på egna koder och skriva egna hemliga meddelanden. VAR FÖRSIKTIG. Andra människor har också läst den här artikeln och de kommer också att bli toppmatematiska kodknäckare. Spioner finns överallt, så var försiktig – vem läser dina meddelanden?
Claire Ellis, författaren till den här artikeln, var chef för Enigmaprojektet, som tar upp koder och kodbrytning, och en äkta Enigma-maskin från andra världskriget, i klassrummet. För mer information kontakta den nya direktören, Claire Greer, via webbplatsen Enigma Schools’ Project.