Magiska kvadrater är kvadratiska rutnät med ett speciellt arrangemang av siffror i dem. Dessa nummer är speciella eftersom varje rad, kolumn och diagonal summerar till samma nummer. I exemplet nedan är alltså 15 det magiska talet. Kan du räkna ut detta bara genom att veta att kvadraten använder siffrorna från 1 till 9?

Och de två siffrorna som står mittemot varandra över mittensiffran kommer att summera till samma tal. Så i kvadraten ovan är 8 + 2 = 10 , 6 + 4 = 10, 1 + 9 = 10 och 3 + 7 = 10. Varför är det så?
Den magiska kvadratens ”ordning” anger hur många rader och kolumner den har. Så en kvadrat med 3 rader och kolumner är ordning 3, och en kvadrat med 4 rader och kolumner är ordning 4 och så vidare. Om du vill veta mer om hur du kan skapa dina egna magiska kvadrater, och om matematiken bakom det hela, kan du gå till några andra sidor på webbplatsen, t.ex. magiska kvadrater och magiska kvadrater II .
Men varför kallas de magiska?
Så siffrorna i den magiska kvadraten är speciella, men varför kallas de magiska? Det verkar som om de sedan urminnes tider var kopplade till den övernaturliga och magiska världen. Den tidigaste uppgiften om magiska kvadrater är från Kina omkring 2200 f.Kr. och kallas ”Lo-Shu”. Det finns en legend som säger att kejsaren Yu såg denna magiska kvadrat på ryggen av en gudomlig sköldpadda i Gula floden.
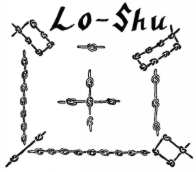
De svarta knutarna visar jämna tal och de vita knutarna visar udda tal. Titta noga och du kommer att se att denna gamla magiska kvadrat är densamma som vårt exempel ovan. Magiska kvadrater nämns för första gången i västvärlden i Theon av Smyrna. De användes också av arabiska astrologer på 800-talet för att hjälpa till att utarbeta horoskop. Den grekiske matematikern Moschopoulos arbete år 1300 e.Kr. bidrog till att sprida kunskapen om magiska kvadrater. Så här är vi nu, mer än 700 år senare, och lärare använder dem i klassen för problemlösning och för att öva addition.
Du kan göra liknande magiska kvadrater, av ordning 3, med hjälp av olika tal. Kan du se några mönster i de nummer som fungerar?