Projektioner
Nu när vi har beskrivit begreppet dimensionsminskning och några av tillämpningarna av SVD och huvudkomponentanalys fokuserar vi på mer detaljer kring matematiken bakom dessa. Vi börjar med projektioner. En projektion är ett begrepp inom linjär algebra som hjälper oss att förstå många av de matematiska operationer vi utför på högdimensionella data. För mer detaljer kan du gå igenom projektioner i en bok om linjär algebra. Här ger vi en snabb genomgång och ger sedan några dataanalysrelaterade exempel.
Som en genomgång, kom ihåg att projektioner minimerar avståndet mellan punkter och underrymden.

I figuren ovan pekar punkten överst på en punkt i rummet. I just den här teckningen är rummet tvådimensionellt, men vi bör tänka abstrakt. Rymden representeras av den kartesiska planen och linjen som den lilla personen står på är ett underrum av punkter. Projektionen till detta delområde är den plats som ligger närmast den ursprungliga punkten. Geometrin säger oss att vi kan hitta denna närmaste punkt genom att släppa en vinkelrät linje (streckad linje) från punkten till utrymmet. Den lilla personen står på projektionen. Den sträcka som denna person var tvungen att gå från ursprunget till den nya projicerade punkten kallas koordinat.
För förklaringen av projektioner kommer vi att använda den vanliga matrisalgebra-notationen för punkter: är en punkt i ett -dimensionellt rum och är mindre delutrymme.
Enkel exempel med N=2
Om vi låter . Vi kan plotta den så här:
mypar (1,1)plot(c(0,4),c(0,4),xlab="Dimension 1",ylab="Dimension 2",type="n")arrows(0,0,2,3,lwd=3)text(2,3," Y",pos=4,cex=3)
Vi kan genast definiera ett koordinatsystem genom att projicera denna vektor till det rum som definieras av: (x-axeln) och (y-axeln). Projektionerna av till det delutrymme som definieras av dessa punkter är 2 respektive 3:
Vi säger att och är koordinaterna och att är baserna.
Nu ska vi definiera ett nytt delutrymme. Den röda linjen i diagrammet nedan är delmängden definierad av punkter som uppfyller med . Projektionen av på är den närmaste punkten på till . Vi måste alltså hitta den som minimerar avståndet mellan och . I linjär algebra lär vi oss att skillnaden mellan dessa punkter är ortogonal till utrymmet så:
Detta innebär att:
och:
Här representerar pricken punktprodukten: .
Följande R-kod bekräftar att ekvationen fungerar:
mypar(1,1)plot(c(0,4),c(0,4),xlab="Dimension 1",ylab="Dimension 2",type="n")arrows(0,0,2,3,lwd=3)abline(0,0.5,col="red",lwd=3) #if x=2c and y=c then slope is 0.5 (y=0.5x)text(2,3," Y",pos=4,cex=3)y=c(2,3)x=c(2,1)cc = crossprod(x,y)/crossprod(x)segments(x*cc,x*cc,y,y,lty=2)text(x*cc,x*cc,expression(hat(Y)),pos=4,cex=3)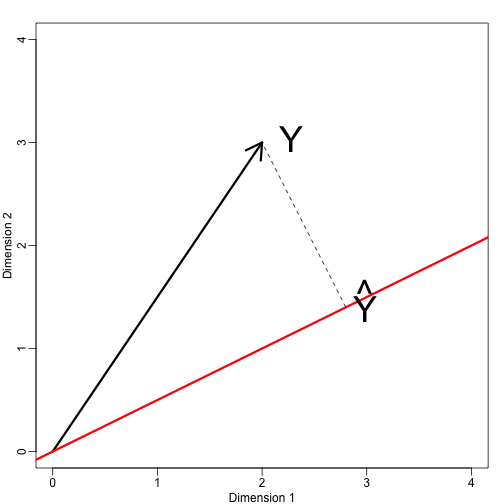
Notera att om var så att , då är helt enkelt och utrymmet ändras inte. Denna förenkling är en anledning till att vi gillar ortogonala matriser.
Exempel:
Låt och är det utrymme som spänns upp av:
I detta utrymme är alla komponenter av vektorerna samma antal, så vi kan tänka oss att detta utrymme representerar konstanterna: i projektionen kommer varje dimension att vara samma värde. Så vad minimerar avståndet mellan och ?
När vi talar om problem som detta använder vi ibland tvådimensionella figurer som den ovan. Vi abstraherar helt enkelt och tänker på som en punkt i och som ett delområde som definieras av ett mindre antal värden, i det här fallet bara ett: .
För att återgå till vår fråga vet vi att projektionen är:
vilket i det här fallet är medelvärdet:
Här hade det också varit lika enkelt att använda kalkyl:
Exempel: Regression är också en projektion
Låt oss ge ett lite mer komplicerat exempel. Enkel linjär regression kan också förklaras med projektioner. Våra data (vi kommer inte längre att använda notationen) är återigen en vektor och vår modell förutsäger med en linje . We want to find the and that minimize the distance between and the space defined by:
with:
Our matrix is and any point in can be written as .
The equation for the multidimensional version of orthogonal projection is:
which we have seen before and gives us:
And the projection to is therefore: