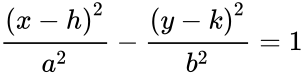av: adminPublicerat den:

Semi-major axel

File:Semimajoraxis.png

Den semimajoralaxeln för en ellips

Inom geometri används begreppet semimajoralaxel (även semimajoralaxel) för att beskriva dimensionerna hos ellipser och hyperbolae.

Ellips

En ellips’ huvudaxel är dess längsta diameter, en linje som går genom centrum och båda fokalerna och vars ändar befinner sig vid formens bredaste punkter. Den halva huvudaxeln är hälften av huvudaxeln och går alltså från centrum, genom ett fokus och till kanten av ellipsen.

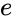
Den är relaterad till den halva huvudaxeln {\displaystyle b\,\!} genom excentriciteten {\displaystyle e\,\!} och semi-latus rectum {\displaystyle \ell \ell \,\!} på följande sätt:

{\displaystyle b=a{\sqrt {1-e^{2}}}}\,\!}{\displaystyle \ell =a(1-e^{2})\,\!}{\displaystyle a\ell =b^{2}\,\!}.

En parabel kan erhållas som gränsen för en sekvens av ellipser där ett fokus hålls fast medan det andra tillåts röra sig godtyckligt långt bort i en riktning, samtidigt som {\displaystyle \ell \,\!} hålls fast. Således tenderar {\displaystyle a\,\!} och {\displaystyle b\,\!} mot oändligheten, {\displaystyle a\,\!} snabbare än {\\displaystyle b\,\!}.

Den halva huvudaxeln är medelvärdet av de minsta och största avstånden från ett fokus till punkterna på ellipsen. Betrakta nu ekvationen i polära koordinater, med ett fokus vid ursprunget och det andra på den positiva x-axeln,

{\displaystyle r(1-e\cos \theta )=l\,\!}

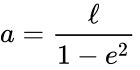
The mean value of {\displaystyle r={\ell \over {1+e}}\,\!} and {\displaystyle r={\ell \over {1-e}}\,\!}, is {\displaystyle a={\ell \over {1-e^{2}}}\,\!}.

Hyperbola

The semi-major axis of a hyperbola is one half of the distance between the two branches; if this is a in the x-direction the equation is:

{\displaystyle {\frac {\left(x-h\right)^{2}}{a^{2}}}-{\frac {\left(y-k\right)^{2}}{b^{2}}}=1}

In terms of the semi-latus rectum and the eccentricity we have

{\displaystyle a={\ell \over e^{2}-1}}

Astronomy

Orbital period

In astrodynamics the orbital period 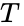{\displaystyle T\,} of a small body orbiting a central body in a circular or elliptical orbit is:

{\displaystyle T=2\pi {\sqrt {a^{3}/\mu }}}

where:

{\displaystyle a\,} är längden på banans halva huvudaxel {\displaystyle \mu } är den vanliga gravitationsparametern

Bemärk att för alla ellipser med en given halva huvudaxel är omloppstiden densamma, oavsett excentricitet.

I astronomin är den halva huvudaxeln en av de viktigaste banelementen för en omloppsbana, tillsammans med dess omloppsperiod. För objekt i solsystemet relateras semimajoraxeln till banans period genom Keplers tredje lag (ursprungligen empiriskt härledd),

{\displaystyle T^{2}=a^{3}\,}

där T är perioden i år, och a är semimajoraxeln i astronomiska enheter. Denna form visar sig vara en förenkling av den allmänna formen för tvåkroppsproblemet, som bestämdes av Newton:

{\displaystyle T^{2}={\frac {4\pi ^{2}}}{G(M+m)}}a^{3}\,}

varvid G är gravitationskonstanten, och M är massan av den centrala kroppen, och m är massan av den kretsande kroppen. Vanligtvis är den centrala kroppens massa så mycket större än den kretsande kroppens att m kan ignoreras. Om man gör detta antagande och använder typiska astronomiska enheter får man den enklare form som Kepler upptäckte.

Märkligt nog är banan för den omgivande kroppen runt barycentret och dess bana i förhållande till sin primära kropp båda ellipser. Den halvmajoraxel som används inom astronomin är alltid avståndet mellan primär och sekundär; planeternas banparametrar anges alltså i heliocentriska termer. Skillnaden mellan primocentriska och ”absoluta” banor kan bäst illustreras genom att titta på jord-mån-systemet. Massförhållandet i detta fall är 81,30059. Det karakteristiska avståndet mellan jorden och månen, den geocentriska månbanans halva huvudaxel, är 384 400 km. Den barycentriska månbanan har å andra sidan en halvstor axel på 379 700 km, och jordens motorbana tar upp skillnaden, 4 700 km. Månens genomsnittliga barycentriska banhastighet är 1,010 km/s, medan jordens är 0,012 km/s. Summan av dessa hastigheter ger den geocentriska månens genomsnittliga omloppshastighet, 1,022 km/s. Samma värde kan erhållas genom att bara betrakta det geocentriska halvmajoraxelvärdet.

Genomsnittligt avstånd

Det sägs ofta att halvmajoraxeln är det ”genomsnittliga” avståndet mellan primären (ellipsens fokus) och den omloppande kroppen. Detta är inte helt korrekt, eftersom det beror på vad genomsnittet tas över.

  • Avsnittet av avståndet över den excentriska anomalin (q.v.) resulterar faktiskt i den halva huvudaxeln.
  • Medelvärdeberäkning över den sanna anomalin (den sanna banvinkeln, mätt i fokus) resulterar, märkligt nog, i den halvminora axeln {\displaystyle b=a{\sqrt {1-e^{2}}}\,\!}.
  • Genomsnittet över den genomsnittliga anomalin (den del av omloppstiden som har förflutit sedan pericentrum, uttryckt som en vinkel) ger slutligen tidsgenomsnittet (vilket är vad ”genomsnitt” vanligtvis betyder för lekmannen): {\displaystyle a(1+{{\frac {e^{2}}}{2}}})\,\!}.

Tidsgenomsnittet av radien invers, {\displaystyle r^{-1}\,\!}, är {\displaystyle a^{-1}\,\!}.

Energi; beräkning av semimajoraxel från tillståndsvektorer

I astrodynamiken kan semimajoraxel {\displaystyle a\,} beräknas från banans tillståndsvektorer:

{\displaystyle a={-\mu \over {2\epsilon }}\,} for an elliptical orbit and {\displaystyle a={\mu \over {2\epsilon }}\,} for a hyperbolic trajectory

and

{\displaystyle \epsilon ={v^{2} \over {2}}-{\mu \over \left|\mathbf {r} \right|}} (specific orbital energy)

and

{\displaystyle \mu =GM\,} (standard gravitational parameter),

where:

  • {\displaystyle v\,} is orbital velocity from velocity vector of an orbiting object,
  • {\displaystyle \mathbf {r} \,} is cartesian position vector of an orbiting object in coordinates of a reference frame with respect to which the elements of the orbit are to be calculated (e.g. geocentrisk ekvatorial för en bana runt jorden, eller heliocentrisk ekliptik för en bana runt solen),
  • {\displaystyle G\,} är gravitationskonstanten,
  • {\displaystyle M\,} massan av den centrala kroppen.

Bemärk att för en given centralkropp och total specifik energi är halvmajoraxeln alltid densamma, oavsett excentricitet. Omvänt är den totala specifika energin alltid densamma för en given centralkropp och en given halvstor axel.

Exempel

Den internationella rymdstationen har en omloppstid på 91,74 minuter, och därmed är den halvstora axeln 6738 km . Varje minut mer motsvarar ca 50 km mer: den extra 300 km långa omloppsbanan tar 40 sekunder, den lägre hastigheten står för ytterligare 20 sekunder.

Lämna ett svar

Din e-postadress kommer inte publiceras. Obligatoriska fält är märkta *