Proiezioni
Ora che abbiamo descritto il concetto di riduzione delle dimensioni e alcune delle applicazioni di SVD e analisi delle componenti principali, ci concentriamo su più dettagli relativi alla matematica che sta dietro a queste. Iniziamo con le proiezioni. Una proiezione è un concetto di algebra lineare che ci aiuta a capire molte delle operazioni matematiche che eseguiamo sui dati ad alta dimensione. Per maggiori dettagli, potete rivedere le proiezioni in un libro di algebra lineare. Qui forniamo un rapido ripasso e poi forniamo alcuni esempi relativi all’analisi dei dati.
Come ripasso, ricordate che le proiezioni minimizzano la distanza tra punti e sottospazio.

Nella figura sopra, il punto in alto sta indicando un punto nello spazio. In questa particolare vignetta, lo spazio è bidimensionale, ma dovremmo pensare in modo astratto. Lo spazio è rappresentato dal piano cartesiano e la linea su cui sta la piccola persona è un sottospazio di punti. La proiezione in questo sottospazio è il luogo più vicino al punto originale. La geometria ci dice che possiamo trovare questo punto più vicino facendo cadere una linea perpendicolare (linea tratteggiata) dal punto allo spazio. La piccola persona è in piedi sulla proiezione. La quantità che questa persona ha dovuto camminare dall’origine al nuovo punto proiettato si chiama coordinata.
Per la spiegazione delle proiezioni, useremo la notazione standard dell’algebra matriciale per i punti: è un punto nello spazio -dimensionale ed è un sottospazio più piccolo.
Esempio semplice con N=2
Se lasciamo che . Possiamo tracciarlo così:
mypar (1,1)plot(c(0,4),c(0,4),xlab="Dimension 1",ylab="Dimension 2",type="n")arrows(0,0,2,3,lwd=3)text(2,3," Y",pos=4,cex=3)
Possiamo immediatamente definire un sistema di coordinate proiettando questo vettore nello spazio definito da: (l’asse x) e (l’asse y). Le proiezioni di al sottospazio definito da questi punti sono rispettivamente 2 e 3:
Diciamo che e sono le coordinate e che sono le basi.
Ora definiamo un nuovo sottospazio. La linea rossa nel grafico qui sotto è il sottoinsieme definito dai punti che soddisfano con . La proiezione di onto è il punto più vicino a . Quindi dobbiamo trovare il che minimizza la distanza tra e . In algebra lineare, impariamo che la differenza tra questi punti è ortogonale allo spazio così:
questo implica che:
e:
Qui il punto rappresenta il prodotto dei punti: .
Il seguente codice R conferma che questa equazione funziona:
mypar(1,1)plot(c(0,4),c(0,4),xlab="Dimension 1",ylab="Dimension 2",type="n")arrows(0,0,2,3,lwd=3)abline(0,0.5,col="red",lwd=3) #if x=2c and y=c then slope is 0.5 (y=0.5x)text(2,3," Y",pos=4,cex=3)y=c(2,3)x=c(2,1)cc = crossprod(x,y)/crossprod(x)segments(x*cc,x*cc,y,y,lty=2)text(x*cc,x*cc,expression(hat(Y)),pos=4,cex=3)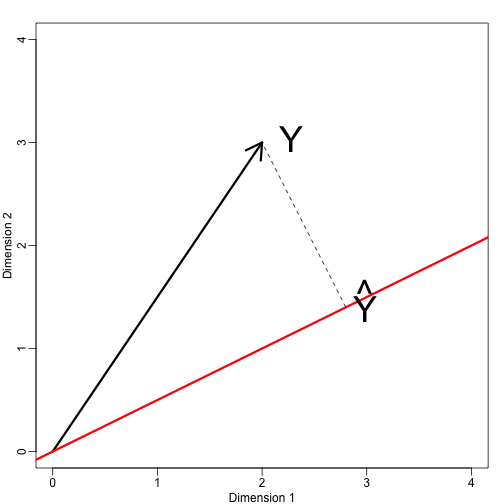
Nota che se era tale che , allora è semplicemente e lo spazio non cambia. Questa semplificazione è uno dei motivi per cui ci piacciono le matrici ortogonali.
Esempio: La media del campione è una proiezione
Lasciamo che e sia lo spazio attraversato da:
In questo spazio, tutte le componenti dei vettori sono lo stesso numero, quindi possiamo pensare a questo spazio come se rappresentasse le costanti: nella proiezione ogni dimensione avrà lo stesso valore. Quindi cosa minimizza la distanza tra e ?
Quando si parla di problemi come questo, a volte usiamo figure bidimensionali come quella sopra. Semplicemente astraiamo e pensiamo ad un punto in e come ad un sottospazio definito da un numero minore di valori, in questo caso uno solo: .
Tornando alla nostra domanda, sappiamo che la proiezione è:
che in questo caso è la media:
Qui, sarebbe stato altrettanto facile usare il calcolo:
Esempio: La regressione è anche una proiezione
Facciamo un esempio leggermente più complicato. La regressione lineare semplice può anche essere spiegata con delle proiezioni. I nostri dati (non useremo più la notazione) sono di nuovo un vettore e il nostro modello predice con una linea. We want to find the and that minimize the distance between and the space defined by:
with:
Our matrix is and any point in can be written as .
The equation for the multidimensional version of orthogonal projection is:
which we have seen before and gives us:
And the projection to is therefore: