ここ数日、数学界は、フィールズ賞やアーベル賞を受賞した有名なマイケル・アティーヤ卿がリーマン仮説を解決したと主張するニュースで沸き返っています。
彼の証明が正しいことが判明すれば、これは長年にわたる最も重要な数学的成果の 1 つとなります。 実際、これは1994年のフェルマーの最終定理の証明や2002年のポアンカレ予想の証明に匹敵する、数学における最大の成果のひとつとなるでしょう。
数学における偉大な未解決問題の 1 つであり、したがって、それを解決した人に栄光がもたらされるだけでなく、リーマン仮説は Clay Mathematics Institute の「ミリオンダラー問題」の 1 つでもあります。 解ければ100万ドルという大金を手にすることができるのだ。
リーマン仮説は、素数の分布と関係があります。素数とは、3、5、7、11などのように、自分自身と1だけで割り切れる整数のことです。 私たちは、素数が無限にあることをギリシア人から聞いて知っています。 しかし、素数が整数内でどのように分布しているかは分かっていない。
この問題は、いわゆる「素数π」関数(与えられた数より小さい素数の数を求める方程式)の推定に端を発しています。 しかし、1858 年にドイツの数学者ベルンハルト・リーマンが行った現代的な再定式化は、現在リーマンのゼータ関数として知られているもののゼロの位置と関係があります。
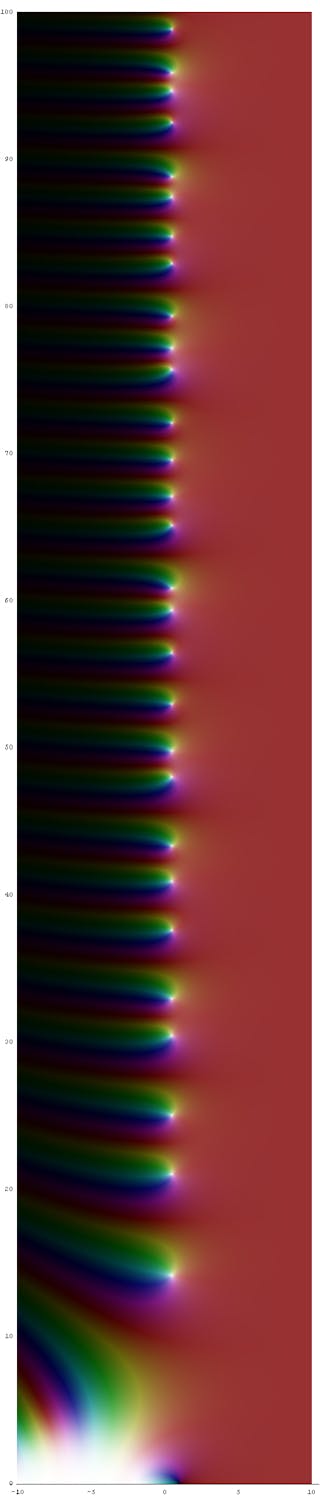
リーマン仮説の技術的な声明は「臨界帯にあるリーマンゼータ関数のゼロは、臨界線上にあるはずだ」です。 この文を理解するにも、複素解析学の大学院レベルの数学のコースが必要です。
ほとんどの数学者は、リーマン仮説が本当に正しいと信じています。 これまでの計算では、臨界線上にない行儀の悪いゼロは見つかっていません。 しかし、確認すべきゼロは無限にあるので、コンピュータの計算では、すべてを確認することはできません。 抽象的な証明しかできない。
もし、リーマン仮説が正しくないとしたら、素数の分布に関する数学者の現在の考え方は大きく外れてしまい、素数について真剣に考え直さなければならないでしょう。
リーマン仮説は、数学界の大物たちによって1世紀半以上にわたって検証されており、経験の浅い数学者が暇つぶしで遊べるような問題ではありません。 この問題の検証には、複雑系解析の非常に深い道具が多く使われ、数学界の名士たちによって行われる非常に真剣なものであるのが普通です。
Atiyahは9月25日にドイツで講演を行い、リーマン仮説を検証するための彼のアプローチの概要を発表しました。 このアウトラインは、しばしば解決策の最初の発表となりますが、問題が解決されたとは受け取られるべきではありません–そうではありません。 私のような数学者にとっては、「証明はプリンにあり」であり、アティヤの解決策が正しいと社会が認めるまでには、多くの段階を踏む必要がある。 まず、解答の詳細を記した原稿を回覧しなければならない。 そして、その証明を検証するという骨の折れる作業が待っている。 これにはかなりの時間がかかるだろう。数ヶ月、あるいは数年かかるかもしれない。
リーマンの仮説に対するAtiyahの試みは真剣なのでしょうか? おそらくそうでしょう。 彼の評判は上々で、それをやり遂げるだけの能力があることは確かです。 一方、この問題に対する他の真剣な試みは、うまくいかなかったものがいくつかあります。 ある時点で、Atiyahは専門家が虱潰しにチェックできるような原稿を回覧する必要があるでしょう。