De afgelopen dagen is de wiskundewereld in rep en roer geraakt door het nieuws dat Sir Michael Atiyah, de beroemde Fields Medalist en Abel Prize-winnaar, beweert de Riemann-hypothese te hebben opgelost.
Als zijn bewijs correct blijkt te zijn, zou dit een van de belangrijkste wiskundige successen in vele jaren zijn. In feite zou dit een van de grootste resultaten in de wiskunde zijn, vergelijkbaar met het bewijs van de Laatste Stelling van Fermat uit 1994 en het bewijs van het Conjectuur van Poincare uit 2002.
De Riemann-hypothese is niet alleen een van de grote onopgeloste problemen in de wiskunde en dus roem voor degene die het oplost, maar het is ook een van de “Million Dollar Problems” van het Clay Mathematics Institute. Een oplossing zou zeker een behoorlijk lucratieve vangst opleveren: een miljoen dollar.
De Riemann-hypothese heeft te maken met de verdeling van de priemgetallen, de gehele getallen die alleen door zichzelf en één gedeeld kunnen worden, zoals 3, 5, 7, 11 enzovoort. Van de Grieken weten we dat er oneindig veel priemgetallen zijn. Wat we niet weten is hoe ze verdeeld zijn binnen de gehele getallen.
Het probleem ontstond bij het schatten van de zogenaamde “priem pi”-functie, een vergelijking om het aantal priemgetallen kleiner dan een bepaald getal te vinden. Maar de moderne herformulering, door de Duitse wiskundige Bernhard Riemann in 1858, heeft te maken met de plaats van de nulpunten van wat nu bekend staat als de Riemann zeta-functie.
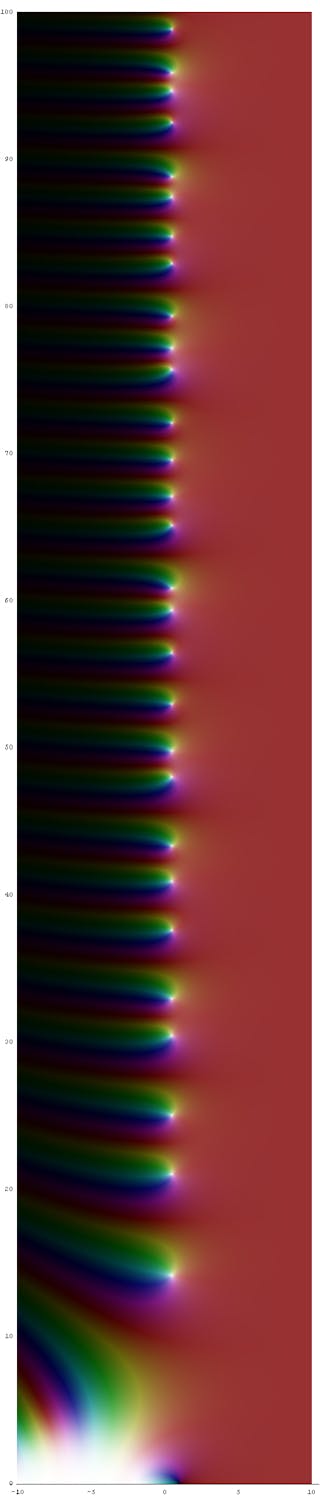
De technische verklaring van de Riemann-hypothese is “de nullen van de Riemann zeta-functie die in de kritische strook liggen, moeten op de kritische lijn liggen”. Zelfs om die uitspraak te begrijpen, moet je wiskundecursussen in complexe analyse volgen.
De meeste wiskundigen geloven dat de Riemann-hypothese inderdaad waar is. Berekeningen hebben tot nu toe geen foutieve nulpunten opgeleverd die niet in de kritische lijn liggen. Er zijn echter oneindig veel van die nullen te controleren, en dus zal een computerberekening niet veel verifiëren. Alleen een abstract bewijs is voldoende.
Als de Riemann-hypothese inderdaad niet waar zou zijn, dan zou het huidige denken van wiskundigen over de verdeling van de priemgetallen er ver naast zitten, en zouden we de priemgetallen serieus moeten heroverwegen.
De Riemann-hypothese wordt al meer dan anderhalve eeuw onderzocht door enkele van de grootste namen uit de wiskunde en is niet het soort probleem waar een onervaren wiskundestudent in zijn of haar vrije tijd mee kan spelen. Pogingen om het te verifiëren vergen veel zeer diepgaande hulpmiddelen uit de complexe analyse en zijn meestal zeer serieus gedaan door enkele van de beste namen in de wiskunde.
Atiyah heeft op 25 sept. in Duitsland een lezing gehouden waarin hij een schets gaf van zijn aanpak om de Riemann-hypothese te verifiëren. Deze schets is vaak de eerste aankondiging van de oplossing, maar moet niet worden opgevat als een oplossing van het probleem – verre van dat. Voor wiskundigen zoals ik zit het “bewijs in de pudding”, en er moeten nog vele stappen worden genomen voordat de gemeenschap de oplossing van Atiyah als correct zal bestempelen. Eerst zal hij een manuscript moeten laten circuleren waarin hij zijn oplossing uiteenzet. Dan is er nog de moeizame taak om zijn bewijs te verifiëren. Dat kan heel wat tijd in beslag nemen, misschien wel maanden of zelfs jaren.
Is Atiyah’s poging tot de Riemann-hypothese serieus? Misschien. Hij heeft een uitstekende reputatie, en hij is zeker capabel genoeg om het voor elkaar te krijgen. Aan de andere kant, er zijn verschillende andere serieuze pogingen geweest om dit probleem op te lossen, maar dat is niet gelukt. Op een gegeven moment zal Atiyah een manuscript moeten laten rondgaan dat deskundigen met een fijne kam kunnen controleren.