W ciągu ostatnich kilku dni świat matematyki zawrzał na wieść o tym, że Sir Michael Atiyah, słynny medalista Fieldsa i laureat Nagrody Abla, twierdzi, że rozwiązał hipotezę Riemanna.
Jeśli jego dowód okaże się poprawny, będzie to jedno z najważniejszych osiągnięć matematycznych od wielu lat. W rzeczywistości byłby to jeden z największych wyników w matematyce, porównywalny z dowodem ostatniego twierdzenia Fermata z 1994 roku i dowodem twierdzenia Poincarego z 2002 roku.
Prócz tego, że hipoteza Riemanna jest jednym z wielkich nierozwiązanych problemów w matematyce i dlatego przyniesie chwałę osobie, która ją rozwiąże, jest też jednym z „problemów miliona dolarów” Clay Mathematics Institute. Jej rozwiązanie z pewnością przyniosłoby całkiem pokaźny zysk: milion dolarów.
Hipoteza Riemanna dotyczy rozkładu liczb pierwszych, tych liczb całkowitych, które mogą być podzielne tylko przez siebie i przez jeden, jak 3, 5, 7, 11 i tak dalej. Wiemy od Greków, że jest nieskończenie wiele liczb pierwszych. Nie wiemy jednak, jak są one rozmieszczone w liczbach całkowitych.
Problem wziął się z szacowania tak zwanej funkcji „prime pi”, równania pozwalającego znaleźć liczbę liczb pierwszych mniejszych od danej liczby. Jednak jego współczesne sformułowanie, dokonane przez niemieckiego matematyka Bernharda Riemanna w 1858 roku, dotyczy położenia zer funkcji znanej obecnie jako funkcja zeta Riemanna.
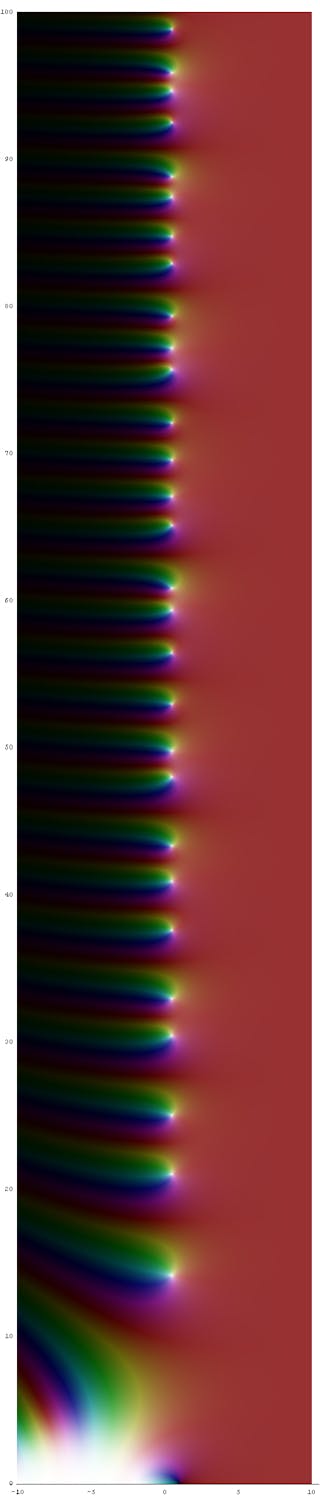
Techniczne stwierdzenie hipotezy Riemanna brzmi: „zera funkcji zeta Riemanna, które leżą w pasie krytycznym, muszą leżeć na linii krytycznej”. Nawet zrozumienie tego stwierdzenia wymaga kursów matematyki na poziomie absolwenta z zakresu analizy złożonej.
Większość matematyków wierzy, że hipoteza Riemanna jest rzeczywiście prawdziwa. Obliczenia do tej pory nie przyniosły żadnych niepoprawnie zachowujących się zer, które nie leżą w linii krytycznej. Jednak tych zer jest nieskończenie wiele, więc obliczenia komputerowe nie sprawdzą aż tak wiele. Wystarczy abstrakcyjny dowód.
Jeśli w rzeczywistości hipoteza Riemanna nie byłaby prawdziwa, to obecne myślenie matematyków o rozkładzie liczb pierwszych byłoby dalekie od prawdy i musielibyśmy poważnie przemyśleć kwestię liczb pierwszych.
Hipoteza Riemanna była badana przez ponad półtora wieku przez największe nazwiska w matematyce i nie jest to problem, z którym niedoświadczony student matematyki może się bawić w wolnym czasie. Próby jego weryfikacji angażują wiele bardzo głębokich narzędzi analizy złożonej i są zazwyczaj bardzo poważne, podejmowane przez jedne z najlepszych nazwisk w matematyce.
Atiyah wygłosił 25 września w Niemczech wykład, w którym przedstawił zarys swojego podejścia do weryfikacji hipotezy Riemanna. Taki zarys jest często pierwszą zapowiedzią rozwiązania, ale nie należy uważać, że problem został rozwiązany – daleko nam do tego. Dla matematyków takich jak ja, „dowód jest w puddingu”, i jest wiele kroków, które muszą być podjęte, zanim społeczność ogłosi rozwiązanie Atiyah jako poprawne. Po pierwsze, będzie on musiał rozprowadzić manuskrypt szczegółowo opisujący jego rozwiązanie. Następnie czeka go żmudne zadanie zweryfikowania dowodu. To może zająć sporo czasu, może miesiące, a nawet lata.
Czy próba Atiyah dotycząca hipotezy Riemanna jest poważna? Być może. Jego reputacja jest znakomita, a on sam jest z pewnością wystarczająco zdolny, by to osiągnąć. Z drugiej strony, było kilka innych poważnych prób rozwiązania tego problemu, które nie wypaliły. W pewnym momencie Atiyah będzie musiał rozprowadzić manuskrypt, który eksperci będą mogli sprawdzić za pomocą grzebienia z drobnymi zębami.