| Astrodynamics | ||
| Orbital mechanics | Equations | Efficiencymeasures |
|---|---|---|
| v · d · e |
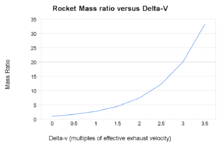
Rocket mass ratios versus velocidade final calculada a partir da equação do foguetão
A equação do foguetão de Tsiolkovsky, ou equação ideal do foguete, é uma equação matemática que relaciona o delta-v (a variação máxima de velocidade do foguete se nenhuma outra força externa agir) com a velocidade efetiva de escape e a massa inicial e final de um motor de reação de outro foguete.Itconsidera o princípio de um foguete: um dispositivo que pode aplicar a aceleração a si mesmo (um impulso) expulsando parte da sua massa com alta velocidade na direcção oposta à da conservação do momento.
Para qualquer manobra deste tipo (ou viagem envolvendo um número de manobras de suchmaneuvers):
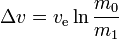
where:
m0 is the initialtotal mass, including propellant. m1 is the finaltotal mass. ve is the effectiveexhaust velocity. (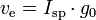 where Isp is the specific impulse expressed as a timeperiod)
where Isp is the specific impulse expressed as a timeperiod) 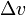 is delta-v-the maximum change of speed of the vehicle (with noexternal forces acting)
is delta-v-the maximum change of speed of the vehicle (with noexternal forces acting)
Units used for mass or velocity do not matter as long as they areconsistent.
- 1 History
- 2 Stages
- 3 Energy
- 4 Derivation
- 5 Examples
- 6 Applicability
- 7 See also
- 8 References
- 9 External links
History
This equation was independently derived by Konstantin Tsiolkovsky towards theend of the 19th century and is widely known under this name and idealrocket equation. Contudo, um panfleto recentemente descoberto “A Treatiseon the Motion of Rockets” por William Mooreshows mostra que a primeira derivação conhecida deste tipo de equação foi na Royal Military Academy atWoolwichin England em 1813, e foi usada para pesquisa de armas.
Etapas
No caso de seqüencialmente empurrando estágios de foguete, a equação se aplica para cada estágio, onde para cada estágio a massa inicial da equação é a massa total do foguete após descartar o estágio anterior, e a massa final na equação é a massa total do foguete imediatamente antes de descartar o estágio em questão. Para cada estágio, o impulso específico pode ser diferente.
Por exemplo, se 80% da massa de um foguete é o combustível do primeiro estágio, e 10% é a massa seca do primeiro estágio, e 10% é o foguete principal, então
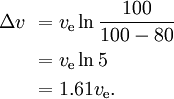
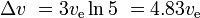
e a carga útil é 10%*10%*10% = 0,1% da massa inicial.
Um foguete SSTO comparável, também com uma carga de 0,1%pay, poderia ter uma massa de 11% para tanques de combustível e motores, e 88,9% para combustível. Isto daria
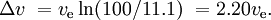
Se o motor de um novo estágio for inflamado antes do estágio anterior ter sido descartado e os motores em funcionamento simultâneo tiverem um impulso específico diferente (como é frequentemente o caso de impulsionadores de foguetes sólidos e estágio de combustível aliquídico), a situação é mais complicada.
Energia
No caso ideal m1 é carga útil e m0 – m1 é massa de reação (isto corresponde a tanques vazios sem massa,etc.). A energia necessária pode simplesmente ser calculada como
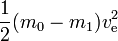
Isto corresponde à energia cinética que a massa de reacção expelida teria a uma velocidade igual à velocidade de escape. Se a massa de reacção tivesse de ser acelerada da velocidade zero para a velocidade de escape, a energia de alergia produzida entraria na massa de reacção e nada iria depender do ganho de energia cinética do foguetão e da carga útil. No entanto, se o foguete já se mover e acelerar (a massa de reacção é expelida na direcção oposta à direcção em que o foguete se move) a energia lesskinetic é adicionada à massa de reacção. Para ver isto, se, por exemplo, ve=10 km/s e a velocidade do foguete for 3 km/s, então a velocidade de uma pequena quantidade de massa de reacção gasta muda de 3 para a frente para 7 km/s para a retaguarda. Assim, enquanto a energia necessária é de 50 MJ por kg de massa de reacção, apenas 20 MJ são utilizados para o aumento da velocidade da massa de reacção. Os 30 MJ restantes são o aumento da energia cinética do bolso e da carga útil.
Em geral:
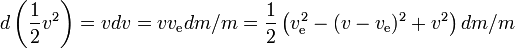
Assim o ganho específico de energia do foguete em qualquer pequeno intervalo de tempo é o ganho de energia do foguete incluindo o combustível restante,dividido pela sua massa, onde o ganho de energia é igual à energia produzida pelo combustível menos o ganho de energia da massa da reação. Quanto maior a velocidade do foguete, menor o ganho de energia da massa de reação; se a velocidade do foguete for mais da metade da velocidade do escape, a massa de reação perde energia ao ser expelida, em benefício do ganho de energia do foguete; quanto maior a velocidade do foguete, maior a perda de energia da massa de reação.
Temos
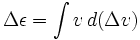
where ε é a energia específica do therocket (potencial mais energia cinética) e Δvis uma variável separada, não apenas a mudança em v.No caso de usar o foguete para desaceleração, ou seja, massa de expulsão na direção da velocidade, v deve ser tomada negativa.
A fórmula é para o caso ideal novamente, sem perda de energia sobreaquecida, etc. Esta última causa uma redução do impulso, portanto é uma vantagem mesmo quando o objetivo é perder energia (desaceleração).
Se a energia é produzida pela própria massa, como numa rocha química, o valor do combustível deve ser 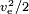 ,onde para o valor do combustível também a massa do oxidante deve ser levada em conta. Um valor típico é ve= 4,5 km/s, correspondendo a um valor de combustível de 10,1 MJ/kg. O valor real do combustível é mais alto, mas grande parte da energia é perdida como calor residual no escape que o bico não foi capaz de extrair.
,onde para o valor do combustível também a massa do oxidante deve ser levada em conta. Um valor típico é ve= 4,5 km/s, correspondendo a um valor de combustível de 10,1 MJ/kg. O valor real do combustível é mais alto, mas grande parte da energia é perdida como calor residual no escape que o bico não foi capaz de extrair.
A energia requerida E é
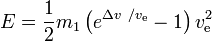
Conclusões:
- for
 temos
temos 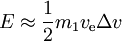
- para um dado Δv, a energia mínima é necessária se ve =0.6275Δv, exigindo uma energia de
E = 0.772m1(Δv)2. A partir da velocidade zero, isto é 54,4 % mais do que apenas a energia cinética da carga útil. Neste caso ideal a massa inicial é 4,92 vezes a massa final.
Estes resultados aplicam-se a uma velocidade de escape fixa.
Due ao efeito Oberth, e partindo de uma velocidade diferente de zero a energia potencial necessária do propulsor pode ser menor o aumento de energia no veículo e da carga útil. Isto pode ser o caso quando a massa de reação tem uma velocidade menor após ser expelida do que antes – foguetes são capazes de liberar alguma ou toda a cinética inicial do propulsor.
Também, para um determinado objetivo, como mover-se de uma órbita para outra, a Δv necessária pode depender muito da taxa a que o motor pode produzir Δv e as manobras podem até ser impossíveis se essa taxa for muito baixa. Por exemplo, um lançamento para LEO normalmente requer um Δv de ca. 9,5 km/s (a maior parte para a velocidade a ser adquirida), mas se o motor pudesse produzir Δv a uma velocidade apenas ligeiramente superior a g,seria um lançamento lento exigindo um Δv muito grande (pense em pairar sem fazer nenhum progresso em velocidade ou altitude, custaria um Δvof 9,8 m/s cada segundo). Se a velocidade possível for apenas g ou menos, a manobra não pode ser feita com este motor.
A potência é dada por
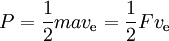
onde F é o impulso e a aceleração devido a ele. Assim, o impulso teoricamente possível por unidade de potência é 2 dividido pelo impulso específico em m/s. A eficiência do impulso é a actualthrust como percentagem disto.
se, por exemplo Se, por exemplo, for utilizada energia solar, isso restringe a; no caso de um ve grande, a aceleração possível é inversamente proporcional a ela, portanto o tempo para atingir um requireddelta-v é proporcional a ve;com 100% de eficiência:
- para
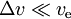 temos
temos 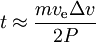
p>Exemplos:
- potência 1000 W, massa 100 kg, Δv=5 km/s, ve=16 km/s, leva 1.5 months.
- power 1000 W, mass 100 kg, Δv=5 km/s, ve=50 km/s, takes 5 months.
Thus ve should notbe too large.
Derivation
Consider the following system:
In the following derivation, “the rocket” is taken to mean “therocket and all of its unburned propellant”. Newton’s second law ofmotion relates external forces (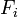 )to the change in linear momentum of the system as follows:
)to the change in linear momentum of the system as follows:
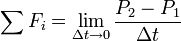
where 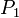 is the momentum of the rocket at time t=0:
is the momentum of the rocket at time t=0:
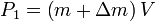
and 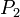 is the momentum of the rocket and exhausted mass at time
is the momentum of the rocket and exhausted mass at time  :
:
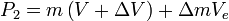
and where, with respect to the observer:
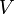 is thevelocity of the rocket at time t=0
is thevelocity of the rocket at time t=0
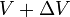 is thevelocity of the rocket at time
is thevelocity of the rocket at time 
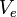 is thevelocity of the mass added to the exhaust (and lost by therocket) during time
is thevelocity of the mass added to the exhaust (and lost by therocket) during time 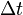
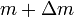 is the massof the rocket at time t=0
is the massof the rocket at time t=0
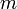 is the massof the rocket at time
is the massof the rocket at time 
The velocity of the exhaust Vein the observer frame is related to the velocity of the exhaust in therocket frame veby
Ve = V − ve
Solving yields:
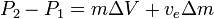
and
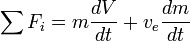
If there are no external forces then 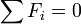 and
and
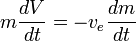 p>assumindo
p>assumindo 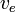 é constante, isto pode ser integrado para render:
é constante, isto pode ser integrado para render: 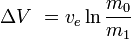
ou equivalente
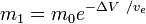 ou
ou 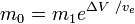
onde m0 é a massa total inicial incluindo o propulsor, e m1 a massa total final e a velocidade do escape do foguete em relação ao foguete (o impulso específico, ou, se medido a tempo, aquele multiplicado pela aceleração gravítica sobre a Terra).
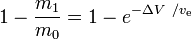 é a massfracção (a parte da massa total inicial que é gasta como massa de reacção).
é a massfracção (a parte da massa total inicial que é gasta como massa de reacção).
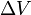 (delta v) é a integração ao longo do tempo da magnitude da aceleração produzida pela utilização do motor de foguete (o que seria a aceleração real se não houvesse forças externas). Espaço livre, para o caso da aceleração no sentido davelocidade, este é o aumento da velocidade. No caso da aceleração em direção oposta (desaceleração) é a diminuição da velocidade.
(delta v) é a integração ao longo do tempo da magnitude da aceleração produzida pela utilização do motor de foguete (o que seria a aceleração real se não houvesse forças externas). Espaço livre, para o caso da aceleração no sentido davelocidade, este é o aumento da velocidade. No caso da aceleração em direção oposta (desaceleração) é a diminuição da velocidade.
Da gravidade do curso e do arrasto também aceleram o veículo, e eles canadenses ou subtraem à mudança de velocidade experimentada pelo veículo. Assim, delta-v não é geralmente a mudança real da velocidade ou velocidade do veículo.
Apesar de uma simplificação extrema, a equação do foguete capta os aspectos essenciais da física do vôo do foguete em uma única equação curta. Também é possível perceber que delta-v é uma das quantidades mais importantes na orbitalmecânica, que quantifica quão difícil é realizar uma determinada manobra orbital.
Claramente, para alcançar um grande delta-v, ou m0m deve ser enorme (crescendo exponencialmente como delta-vrises), ou m1 deve apostar, ou deve beber alto, ou alguma combinação de todos eles.
Na prática, isto foi conseguido usando foguetes muito grandes (aumentando m0), com etapas múltiplas (diminuindo m1),androckets com velocidades de escape muito altas. Os Saturn Vrockets usados no programa espacial Apollo e os propulsores iônicos usados em sondas não tripuladas de longa distância são bons exemplos disso.
A equação do foguete mostra uma espécie de “decadência exponencial” da massa m1, não em função do tempo, mas em função do delta-v produzido. O delta-v que é o “semi-vida” correspondente é 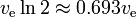
Exemplos
Assumir uma velocidade de escape de 4,5 km/s e um Δv de 9,7 km/s (Terra para LEO).
- Estágio único para o orbitrocket: 1 – e – 9,7 / 4,5= 0,884, portanto 88,4 % da massa total inicial tem de bepropelente. O restante 11,6 % é para os motores, o tanque e a carga útil. No caso de um vaivém espacial, também incluiria theorbiter.
- Dois estágios para orbitar:suponha que o primeiro estágio deve fornecer um Δvof 5.0 km/s; 1 – e – 5.0 / 4.5= 0.671, portanto 67.1% da massa total inicial tem que ser propulsor para o primeiro estágio. A massa restante é de 32,9 %. Após a eliminação do primeiro estágio, uma massa permanece igual a estes 32.9 %, menos a massa do tanque e dos motores da primeira fase. Suponha que isto é 8% da massa total inicial, então 24,9% permanece. Este segundo estágio deve fornecer um Δvof 4,7 km/s; 1 – e – 4,7 / 4,5= 0,648, portanto 64,8% da massa restante tem que ser propulsor,que é 16,2%, e 8,7% permanece para o tanque e motores do segundo estágio, a carga útil, e no caso de um ônibus espacial,também o orbital. Assim, em conjunto, 16,7% está disponível para todos os motores, os tanques, a carga útil e o possível orbitador.
Aplicabilidade
A equação do foguetão é válida para veículos de reacção do tipo foguetão quando a velocidade de escape efectiva é constante; e pode ser somada ou integrada quando a velocidade de escape efectiva varia.
No entanto, não se aplica a outras tecnologias, tais como: canhões de lançamento, elevadores espaciais, lançadores, motores de propulsão por cabo e de respiração de ar.
Ver também
- Delta-v
- Delta-v budget
- Efeito Oberth aplicando delta-v in a gravitywell increases the final velocity
- Specific impulse
- Spacecraft propulsion
- Mass ratio
- Working mass
- Relativistic rocket
- Reversibility oforbits
|
|
This article includes a list of references, but itssources remain unclear because it has insufficient inline citations. Please help to improvethis article by introducing more precise citations where appropriate. (February2009) |
- ^К. Э. Циолковский, Исследование мировых пространств реактивнымиприборами, 1903. It is available online here in a RARed PDF
- ^ Moore, William; ofthe MilitaryAcademy at Woolwich (1813). A Treatise on the Motion ofRockets. To which is added, An Essay on Naval Gunnery. London: G.and S. Robinson.
- ^ Johnson, W. (1995). “Contents and commentary onWilliam Moore’s a treatise on the motion of rockets and an essay onnaval gunnery”. International Journal of Impact Engineering 16 (3): 499–521. doi:10.1016/0734-743X(94)00052-X. ISSN 0734-743X. http://www.sciencedirect.com/science/article/B6V3K-3Y5FP5P-11/2/c3e98a6cec8f083c93dc4e4e157282bb.
- How to derive the rocket equation
- Relativity Calculator – LearnTsiolkovsky’s rocket equations