| Astrodynamics | ||
| Orbital mechanics | Equations | Efficiencymeasures |
|---|---|---|
| v · d · e |
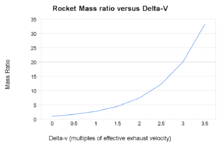
Ratios de masse des fusées en fonction de la vitesse finale calculée à partir de l’équation de la fusée
L’équation de la fusée de Tsiolkovsky, ou équation de la fusée idéale, est une équation mathématique qui relie le delta-v (le changement maximal de vitesse de la fusée si aucune autre force externe n’agit) à la vitesse d’échappement effective et à la masse initiale et finale d’une fusée ou d’un autre moteur à réaction.
L’équation porte le nom de KonstantinTsiolkovsky qui l’a dérivée indépendamment et publiée dans son ouvrage de 1903.Elleconsidère le principe d’une fusée :un dispositif qui peut s’appliquer une accélération à lui-même (une poussée)en expulsant une partie de sa masse à grande vitesse dans la direction opposéeen raison de la conservation de la quantité de mouvement.
Pour toute manœuvre de ce type (ou voyage impliquant un certain nombre de ces manœuvres):
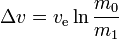
where:
m0 is the initialtotal mass, including propellant. m1 is the finaltotal mass. ve is the effectiveexhaust velocity. (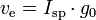 where Isp is the specific impulse expressed as a timeperiod)
where Isp is the specific impulse expressed as a timeperiod)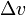 is delta-v-the maximum change of speed of the vehicle (with noexternal forces acting)
is delta-v-the maximum change of speed of the vehicle (with noexternal forces acting)
Units used for mass or velocity do not matter as long as they areconsistent.
- 1 History
- 2 Stages
- 3 Energy
- 4 Derivation
- 5 Examples
- 6 Applicability
- 7 See also
- 8 References
- 9 External links
History
This equation was independently derived by Konstantin Tsiolkovsky towards theend of the 19th century and is widely known under this name and idealrocket equation. Cependant, un pamphlet récemment découvert « A Treatiseon the Motion of Rockets » par William Mooreshows que la plus ancienne dérivation connue de ce type d’équation était en fait à l’Académie militaire royale deWoolwich en Angleterre en 1813,et a été utilisé pour la recherche sur les armes.
Étages
Dans le cas d’étages de fusée à poussée séquentielle, l’équation s’applique pour chaque étage, où pour chaque étage la masse initiale dans l’équation est la masse totale de la fusée après avoir écarté l’étage précédent, et la masse finale dans l’équation est la masse totale de la fusée juste avant d’écarter l’étage concerné. Pour chaque étage, l’impulsion spécifique peut être différente.
Par exemple, si 80 % de la masse d’une fusée est le carburant du premier étage, et 10 % est la masse sèche du premier étage, et 10 % est la fusée restante, alors
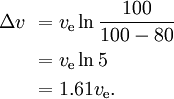
Avec trois étapes similaires, puis plus petites, avec le même ve pour chaque étape, nous avons
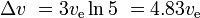
et la charge utile est de 10%*10%*10% = 0,1% de la masse initiale.
Une fusée SSTO comparable, également avec une charge utile de 0,1%, pourrait avoir une masse de 11% pour les réservoirs et les moteurs, et 88,9% pour le carburant. Cela donnerait
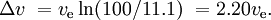
Si le moteur d’un nouvel étage est allumé avant que l’étage précédent ait été mis au rebut et que les moteurs fonctionnant simultanément ont une impulsion spécifique différente (comme c’est souvent le cas avec les propulseurs à poudre et l’étage à combustible liquide), la situation est plus compliquée.
Energie
Dans le cas idéal, m1est la charge utile et m0 – m1est la masse de réaction (cela correspond à des réservoirs vides n’ayant pas de masse,etc). L’énergie nécessaire peut être simplement calculée comme
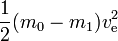
Cela correspond à l’énergie cinétique que la masse de réaction expulsée aurait à une vitesse égale à celle de l’échappement. Si la masse de réaction devait être accélérée de la vitesse zéro à la vitesse d’échappement, toute l’énergie produite irait dans la masse de réaction et il ne resterait rien pour le gain d’énergie cinétique de la fusée et de la charge utile. Cependant, si la fusée se déplace et accélère déjà (la masse de réaction est expulsée dans la direction opposée à celle dans laquelle la fusée se déplace), moins d’énergie cinétique est ajoutée à la masse de réaction. Pour s’en convaincre, si, par exemple, ve=10 km/s et que la vitesse de la fusée est de 3 km/s, la vitesse d’une petite quantité de masse de réaction expulsée passe de 3 vers l’avant à 7 km/s vers l’arrière. Ainsi, alors que l’énergie requise est de 50 MJ par kg de masse de réaction, seuls 20 MJ sont utilisés pour l’augmentation de la vitesse de la masse de réaction. Les 30 MJ restants correspondent à l’augmentation de l’énergie cinétique de la fusée et de la charge utile.
En général :
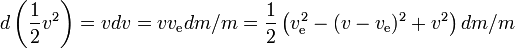
Donc le gain d’énergie spécifique de la fusée dans tout petit intervalle de temps est le gain d’énergie de la fusée incluant le carburant restant,divisé par sa masse, où le gain d’énergie est égal à l’énergie produite par le carburant moins le gain d’énergie de la masse de réaction. Plus la vitesse de la fusée est grande, plus le gain d’énergie de la masse de réaction est faible ; si la vitesse de la fusée est supérieure à la moitié de la vitesse d’échappement, la masse de réaction perd même de l’énergie en étant expulsée, au profit du gain d’énergie de la fusée ; plus la vitesse de la fusée est grande, plus la perte d’énergie de la masse de réaction est importante.
On a
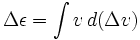
où ε est l’énergie spécifique de la fusée (énergie potentielle plus énergie cinétique) et Δvis une variable distincte, pas seulement la variation de v.Dans le cas de l’utilisation de la fusée pour la décélération, c’est-à-dire l’expulsion de la masse de réaction dans la direction de la vitesse, vdoit être pris négatif.
La formule est à nouveau pour le cas idéal, sans perte d’énergie sur la chaleur, etc. Cette dernière entraîne une réduction de la poussée, c’est donc un inconvénient même lorsque l’objectif est de perdre de l’énergie (décélération).
Si l’énergie est produite par la masse elle-même, comme dans une fusée chimique, la valeur du carburant doit être 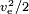 ,où pour la valeur du carburant, il faut également tenir compte de la masse de l’oxydant. Une valeur typique est ve= 4,5 km/s, correspondant à une valeur de combustible de 10,1 MJ/kg. La valeur réelle du carburant est plus élevée, mais une grande partie de l’énergie est perdue sous forme de chaleur résiduelle dans l’échappement que la buse n’a pas pu extraire.
,où pour la valeur du carburant, il faut également tenir compte de la masse de l’oxydant. Une valeur typique est ve= 4,5 km/s, correspondant à une valeur de combustible de 10,1 MJ/kg. La valeur réelle du carburant est plus élevée, mais une grande partie de l’énergie est perdue sous forme de chaleur résiduelle dans l’échappement que la buse n’a pas pu extraire.
L’énergie requise E est
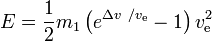
Conclusions :
- pour
 nous avons
nous avons 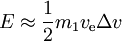
- pour un Δv donné, l’énergie minimale est nécessaire si ve =0.6275Δv, nécessitant une énergie de
E = 0,772m1(Δv)2. En partant d’une vitesse nulle, cela représente 54,4 % de plus que la seule énergie cinétique de la charge utile. Dans ce cas optimal, la masse initiale est4,92 fois la masse finale.
Ces résultats s’appliquent pour une vitesse d’échappement fixe.
En raison de l’effet Oberth, et en partant d’une vitesse non nulle, l’énergie potentielle requise du propergol peut être inférieure à l’augmentation de l’énergie dans le véhicule et la charge utile. Cela peut être le cas lorsque la masse de réaction a une vitesse plus faible après avoir été expulsée qu’avant- les fusées sont capables de libérer une partie ou la totalité de l’énergie cinétique initiale du propergol.
De plus, pour un objectif donné tel que le déplacement d’une orbite à une autre, le Δv requis peut dépendre grandement du taux auquel le moteur peut produire du Δv et les manœuvres peuvent même être impossibles si ce taux est trop faible. Par exemple, un lancement vers LEO nécessite normalement un Δv d’environ 9,5 km/s (principalement pour acquérir la vitesse), mais si le moteur pouvait produire un Δv à un taux à peine supérieur à g, il s’agirait d’un lancement lent nécessitant un Δv très important (pensez au vol stationnaire sans progression de la vitesse ou de l’altitude, cela coûterait un Δv de 9,8 m/s chaque seconde). Si la vitesse possible n’est que de g ou moins, la manœuvre ne peut absolument pas être réalisée avec ce moteur.
La puissance est donnée par
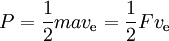
où F est la poussée et a l’accélération qui lui est due. Ainsi, la poussée théoriquement possible par unité de puissance est égale à 2 divisé par l’impulsion spécifique en m/s. L’efficacité de la poussée est la poussée réelle en pourcentage de celle-ci.
Si l’on utilise par ex. l’énergie solaire est utilisée, cela limite a ; dans le cas d’une grande ve, l’accélération possible est inversement proportionnelle à celle-ci, donc le temps pour atteindre une delta-v requise est proportionnel à ve;avec une efficacité de100% :
- pour
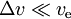 on a
on a 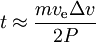
Exemples :
- Puissance 1000 W, masse 100 kg, Δv=5 km/s, ve=16 km/s, prend 1.5 months.
- power 1000 W, mass 100 kg, Δv=5 km/s, ve=50 km/s, takes 5 months.
Thus ve should notbe too large.
Derivation
Consider the following system:
In the following derivation, « the rocket » is taken to mean « therocket and all of its unburned propellant ». Newton’s second law ofmotion relates external forces (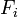 )to the change in linear momentum of the system as follows:
)to the change in linear momentum of the system as follows:
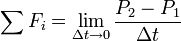
where 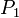 is the momentum of the rocket at time t=0:
is the momentum of the rocket at time t=0:
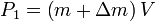
and 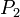 is the momentum of the rocket and exhausted mass at time
is the momentum of the rocket and exhausted mass at time  :
:
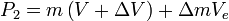
and where, with respect to the observer:
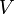 is thevelocity of the rocket at time t=0
is thevelocity of the rocket at time t=0
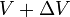 is thevelocity of the rocket at time
is thevelocity of the rocket at time 
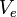 is thevelocity of the mass added to the exhaust (and lost by therocket) during time
is thevelocity of the mass added to the exhaust (and lost by therocket) during time 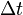
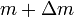 is the massof the rocket at time t=0
is the massof the rocket at time t=0
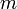 is the massof the rocket at time
is the massof the rocket at time 
The velocity of the exhaust Vein the observer frame is related to the velocity of the exhaust in therocket frame veby
Ve = V − ve
Solving yields:
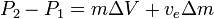
and
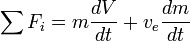
If there are no external forces then 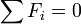 and
and
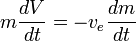
En supposant que 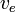 est constant, on peut l’intégrer pour obtenir :
est constant, on peut l’intégrer pour obtenir :
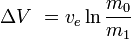
ou de manière équivalente
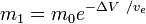 ou
ou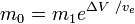
où m0 est la masse totale initiale incluant le propergol, et m1la masse totale finale et vela vitesse de l’échappement de la fusée par rapport à la fusée (l’impulsion spécifique ou, si elle est mesurée dans le temps, celle multipliée par l’accélération terrestre de la gravité).
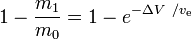 est la fraction de masse (la partie de la masse totale initiale qui est dépensée comme masse de réaction).
est la fraction de masse (la partie de la masse totale initiale qui est dépensée comme masse de réaction).
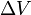 (delta v) est l’intégration dans le temps de la grandeur de l’accélération produite par l’utilisation du moteur de la fusée (ce que serait l’accélération réelle si les forces externes étaient absentes). Dans l’espace libre, pour le cas d’une accélération dans la direction de la vitesse, c’est l’augmentation de la vitesse. Dans le cas d’une accélération en sens inverse (décélération), il s’agit de la diminution de la vitesse.
(delta v) est l’intégration dans le temps de la grandeur de l’accélération produite par l’utilisation du moteur de la fusée (ce que serait l’accélération réelle si les forces externes étaient absentes). Dans l’espace libre, pour le cas d’une accélération dans la direction de la vitesse, c’est l’augmentation de la vitesse. Dans le cas d’une accélération en sens inverse (décélération), il s’agit de la diminution de la vitesse.
Bien sûr, la gravité et la traînée accélèrent également le véhicule, et elles peuvent ajouter ou soustraire à la variation de la vitesse subie par le véhicule.
Donc, le delta-v n’est généralement pas la variation réelle de la vitesse ou de la vélocité du véhicule.
Bien qu’il s’agisse d’une simplification extrême, l’équation de la fusée capture l’essentiel de la physique du vol en fusée en une seule équation courte. Il se trouve également que le delta-v est l’une des quantités les plus importantes en mécanique orbitale, qui quantifie la difficulté d’effectuer une manœuvre orbitale donnée.
Il est clair que pour obtenir un grand delta-v, soit m0doit être énorme (croissant exponentiellement à mesure que le delta-v augmente), soit m1 doit être minuscule, soit ve doit être très élevé, soit une combinaison de tout cela.
Dans la pratique, on y est parvenu en utilisant de très grandes fusées(augmentant m0), à étages multiples (diminuant m1), et des fusées à très haute vitesse d’échappement. Les fusées Saturn V utilisées dans le programme spatial Apollo et les propulseurs ioniques utilisés dans les sondes non habitées à longue distance en sont de bons exemples.
L’équation de la fusée montre une sorte de « décroissance exponentielle » de la masse m1, non pas en fonction du temps, mais en fonction du delta-v produit. Le delta-v qui est la « demi-vie » correspondante est 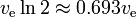
Exemples
Supposons une vitesse d’échappement de 4,5 km/s et un Δv de 9,7 km/s (Terre à LEO).
- Fusée à un seul étage vers l’orbite : 1 – e – 9,7 / 4,5= 0,884, donc 88,4 % de la masse totale initiale doit être du propergol. Les 11,6 % restants sont destinés aux moteurs, au réservoir et à la charge utile. Dans le cas d’une navette spatiale, elle comprendrait également l’orbiteur.
- Deux étages vers l’orbite :supposons que le premier étage doive fournir un Δvde 5,0 km/s ; 1 – e – 5,0 / 4,5= 0,671, donc 67,1 % de la masse totale initiale doit être du propergol au premier étage. La masse restante est de 32,9 %. Après l’élimination du premier étage, il reste une masse égale à ces 32.9 %, moins la masse du réservoir et des moteurs du premier étage. Supposons que cette masse représente 8 % de la masse totale initiale, il reste donc 24,9 %. Le deuxième étage doit fournir un Δvde 4,7 km/s ; 1 – e – 4,7 / 4,5= 0,648, donc 64,8 % de la masse restante doit être constituée de propergol, soit 16,2 %, et 8,7 % reste pour le réservoir et les moteurs du deuxième étage, la charge utile, et dans le cas d’une navette spatiale, également l’orbiteur. Ainsi, ensemble, 16,7 % sont disponibles pour tous les moteurs, les réservoirs, la charge utile et l’éventuel orbiteur.
Applicabilité
L’équation de la fusée est valable pour les véhicules à réaction de type fusée chaque fois que la vitesse d’échappement effective est constante ; et peut être additionnée ou intégrée lorsque la vitesse d’échappement effective varie.
Cependant, elle ne s’applique pas à d’autres technologies telles que les lanceurs à canon, les ascenseurs spatiaux, les boucles de lancement, la propulsion par longeur et les moteurs à air comprimé.
Voir aussi
- Delta-v
- Budget delta-v
- Effet Oberth l’application du delta-.v in a gravitywell increases the final velocity
- Specific impulse
- Spacecraft propulsion
- Mass ratio
- Working mass
- Relativistic rocket
- Reversibility oforbits
|
|
This article includes a list of references, but itssources remain unclear because it has insufficient inline citations. Please help to improvethis article by introducing more precise citations where appropriate. (February2009) |
- ^К. Э. Циолковский, Исследование мировых пространств реактивнымиприборами, 1903. It is available online here in a RARed PDF
- ^ Moore, William; ofthe MilitaryAcademy at Woolwich (1813). A Treatise on the Motion ofRockets. To which is added, An Essay on Naval Gunnery. London: G.and S. Robinson.
- ^ Johnson, W. (1995). « Contents and commentary onWilliam Moore’s a treatise on the motion of rockets and an essay onnaval gunnery ». International Journal of Impact Engineering 16 (3): 499–521. doi:10.1016/0734-743X(94)00052-X. ISSN 0734-743X. http://www.sciencedirect.com/science/article/B6V3K-3Y5FP5P-11/2/c3e98a6cec8f083c93dc4e4e157282bb.
- How to derive the rocket equation
- Relativity Calculator – LearnTsiolkovsky’s rocket equations