| Astrodynamics | ||
| Orbital mechanics | Equations | Efficiencymeasures |
|---|---|---|
| v · d · e |
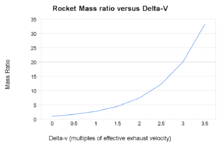
Raketenmassenverhältnisse im Verhältnis zur Endgeschwindigkeit, berechnet aus der Raketengleichung
Die Tsiolkowsky-Raketengleichung, oder ideale Raketengleichung, ist eine mathematische Gleichung, die das Delta-v (die maximale Geschwindigkeitsänderung der Rakete, wenn keine anderen äußeren Kräfte wirken) mit der effektiven Ausstoßgeschwindigkeit und der Anfangs- und Endmasse einer Rakete oder eines anderen Reaktionstriebwerks in Beziehung setzt.
Die Gleichung ist nach Konstantin Tsiolkowsky benannt, der sie in seinem Werk von 1903 unabhängig hergeleitet und veröffentlicht hat.
Sie berücksichtigt das Prinzip einer Rakete: ein Gerät, das sich selbst beschleunigen kann (ein Schub), indem es einen Teil seiner Masse mit hoher Geschwindigkeit in die entgegengesetzte Richtung ausstößt, und zwar aufgrund der Impulserhaltung.
Für ein solches Manöver (oder eine Reise mit einer Reihe solcher Manöver):
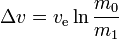
where:
m0 is the initialtotal mass, including propellant. m1 is the finaltotal mass. ve is the effectiveexhaust velocity. (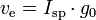 where Isp is the specific impulse expressed as a timeperiod)
where Isp is the specific impulse expressed as a timeperiod)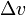 is delta-v-the maximum change of speed of the vehicle (with noexternal forces acting)
is delta-v-the maximum change of speed of the vehicle (with noexternal forces acting)
Units used for mass or velocity do not matter as long as they areconsistent.
- 1 History
- 2 Stages
- 3 Energy
- 4 Derivation
- 5 Examples
- 6 Applicability
- 7 See also
- 8 References
- 9 External links
History
This equation was independently derived by Konstantin Tsiolkovsky towards theend of the 19th century and is widely known under this name and idealrocket equation. Ein kürzlich entdecktes Pamphlet „A Treatiseon the Motion of Rockets“ von William Moor zeigt jedoch, dass die früheste bekannte Ableitung dieser Art von Gleichung 1813 an der Königlichen Militärakademie in Woolwich in England erfolgte und für die Waffenforschung verwendet wurde.
Stufen
Bei nacheinander schiebenden Raketenstufen gilt die Gleichung für jede Stufe, wobei für jede Stufe die Anfangsmasse in der Gleichung die Gesamtmasse der Rakete nach Abwurf der vorhergehenden Stufe und die Endmasse in der Gleichung die Gesamtmasse der Rakete unmittelbar vor Abwurf der betreffenden Stufe ist. Für jede Stufe kann der spezifische Impuls unterschiedlich sein.
Wenn zum Beispiel 80 % der Masse einer Rakete aus dem Treibstoff der ersten Stufe bestehen, 10 % aus der Trockenmasse der ersten Stufe und 10 % aus der restlichen Rakete, dann
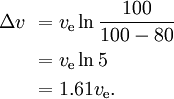
Bei drei ähnlichen, anschließend kleineren Stufen mit dem gleichen ve für jede Stufe haben wir
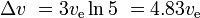
und die Nutzlast beträgt 10%*10%*10% = 0,1% der Ausgangsmasse.
Eine vergleichbare SSTO-Rakete, ebenfalls mit einer Nutzlast von 0,1%, könnte eine Masse von 11% für Tanks und Triebwerke und 88,9% für Treibstoff haben. Dies würde
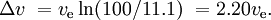
Wenn der Motor einer neuen Stufe gezündet wird, bevor die vorherige Stufe abgeworfen wurde, und die gleichzeitig arbeitenden Motoren einen unterschiedlichen spezifischen Impuls haben (wie es bei Feststoffraketenboostern und Flüssigtreibstoffstufen häufig der Fall ist), ist die Situation komplizierter.
Energie
Im Idealfall ist m1 die Nutzlast und m0 – m1 die Reaktionsmasse (dies entspricht leeren Tanks, die keine Masse haben, usw.). Die benötigte Energie kann einfach berechnet werden als
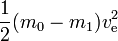
Dies entspricht der kinetischen Energie, die die ausgestoßene Reaktionsmasse bei einer Geschwindigkeit gleich der Ausstoßgeschwindigkeit hätte. Müsste die Reaktionsmasse von der Geschwindigkeit Null auf die Ausstoßgeschwindigkeit beschleunigt werden, würde die gesamte erzeugte Energie in die Reaktionsmasse fließen, und es bliebe nichts mehr für die kinetische Energiegewinnung durch die Rakete und die Nutzlast übrig. Wenn sich die Rakete jedoch bereits bewegt und beschleunigt wird (die Reaktionsmasse wird in die entgegengesetzte Richtung zur Bewegungsrichtung der Rakete ausgestoßen), wird der Reaktionsmasse weniger kinetische Energie zugeführt. Wenn beispielsweise ve=10 km/s und die Geschwindigkeit der Rakete 3 km/s beträgt, dann ändert sich die Geschwindigkeit einer kleinen Menge der ausgestoßenen Reaktionsmasse von 3 km/s vorwärts auf 7 km/s rückwärts. Während also die benötigte Energie 50 MJ pro kg Reaktionsmasse beträgt, werden nur 20 MJ für die Erhöhung der Geschwindigkeit der Reaktionsmasse verwendet. Die restlichen 30 MJ entfallen auf die Erhöhung der kinetischen Energie von Rakete und Nutzlast.
Im Allgemeinen:
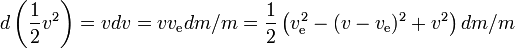
Der spezifische Energiegewinn der Rakete in einem beliebigen kleinen Zeitintervall ist also der Energiegewinn der Rakete einschließlich des restlichen Treibstoffs,geteilt durch ihre Masse, wobei der Energiegewinn gleich der vom Treibstoff erzeugten Energie abzüglich des Energiegewinns der Reaktionsmasse ist. Je größer die Geschwindigkeit der Rakete ist, desto geringer ist der Energiegewinn der Reaktionsmasse; wenn die Geschwindigkeit der Rakete mehr als die Hälfte der Ausstoßgeschwindigkeit beträgt, verliert die Reaktionsmasse beim Ausstoß sogar Energie zugunsten des Energiegewinns der Rakete; je größer die Geschwindigkeit der Rakete, desto größer ist der Energieverlust der Reaktionsmasse.
Wir haben
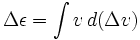
wobei ε die spezifische Energie der Rakete ist (potentielle plus kinetische Energie) und Δeine separate Variable, nicht nur die Änderung von v.Für den Fall, dass die Rakete zum Abbremsen verwendet wird, d.h. Reaktionsmasse in Richtung der Geschwindigkeit ausgestoßen wird, ist v negativ zu nehmen.
Die Formel gilt wieder für den Idealfall, bei dem keine Energie durch Erwärmung etc. verloren geht. Letzteres führt zu einer Verringerung des Schubs, ist also auch dann von Vorteil, wenn das Ziel ein Energieverlust (Verzögerung) ist.
Wird die Energie durch die Masse selbst erzeugt, wie bei einer chemischen Rakete, muss der Treibstoffwert 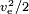 sein, wobei für den Treibstoffwert auch die Masse des Oxidationsmittels berücksichtigt werden muss. Ein typischer Wert ist ve= 4,5 km/s, was einem Brennstoffwert von 10,1 MJ/kg entspricht. Der tatsächliche Brennstoffwert ist höher, aber ein großer Teil der Energie geht als Abwärme im Abgas verloren, die die Düse nicht abführen konnte.
sein, wobei für den Treibstoffwert auch die Masse des Oxidationsmittels berücksichtigt werden muss. Ein typischer Wert ist ve= 4,5 km/s, was einem Brennstoffwert von 10,1 MJ/kg entspricht. Der tatsächliche Brennstoffwert ist höher, aber ein großer Teil der Energie geht als Abwärme im Abgas verloren, die die Düse nicht abführen konnte.
Die benötigte Energie E ist
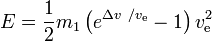
Ausführungen:
- für
 haben wir
haben wir 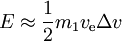
- für ein gegebenes Δv ist die Minimalenergie erforderlich, wenn ve =0.6275Δv, was eine Energie von
E = 0,772m1(Δv)2 erfordert. Ausgehend von der Geschwindigkeit Null sind das 54,4 % mehr als nur die kinetische Energie der Nutzlast. In diesem optimalen Fall ist die Anfangsmasse das 4,92-fache der Endmasse.
Diese Ergebnisse gelten für eine feste Ausstoßgeschwindigkeit.
Aufgrund des Oberth-Effekts kann die erforderliche potenzielle Energie des Treibstoffs beim Start bei einer Geschwindigkeit ungleich Null geringer sein als der Energiezuwachs in Fahrzeug und Nutzlast. Dies kann der Fall sein, wenn die Reaktionsmasse nach dem Ausstoßen eine geringere Geschwindigkeit hat als vorher – Raketen sind in der Lage, einen Teil oder die gesamte anfängliche kinetische Energie des Treibstoffs freizusetzen.
Außerdem kann für ein bestimmtes Ziel, wie z. B. die Bewegung von einer Umlaufbahn in eine andere, die erforderliche Δv stark von der Geschwindigkeit abhängen, mit der das Triebwerk Δv erzeugen kann, und Manöver können sogar unmöglich sein, wenn diese Geschwindigkeit zu niedrig ist. Ein Start zum LEO beispielsweise erfordert normalerweise eine Δv von ca. 9,5 km/s (vor allem für die zu erreichende Geschwindigkeit), aber wenn das Triebwerk nur eine Δv von etwas mehr als g erzeugen könnte, wäre es ein langsamer Start, der insgesamt eine sehr große Δv erfordern würde (man denke an einen Schwebeflug ohne Geschwindigkeits- oder Höhenzuwachs, der jede Sekunde eine Δv von 9,8 m/s kosten würde). Wenn die mögliche Geschwindigkeit nur g oder weniger beträgt, kann das Manöver mit diesem Triebwerk gar nicht durchgeführt werden.
Die Leistung ist gegeben durch
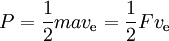
wobei F der Schub ist und a die dadurch bedingte Beschleunigung. Der theoretisch mögliche Schub pro Leistungseinheit ist also 2 geteilt durch den spezifischen Impuls in m/s. Die Schubeffizienz ist der tatsächliche Schub in Prozent davon.
Wenn z.B. Solarenergie verwendet wird, schränkt dies a ein; im Falle eines großen ve ist die mögliche Beschleunigung umgekehrt proportional dazu, daher ist die Zeit zum Erreichen eines erforderlichendelta-v proportional zu ve;bei100% Wirkungsgrad:
- für
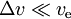 haben wir
haben wir 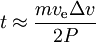
Beispiele:
- Leistung 1000 W, Masse 100 kg, Δv=5 km/s, ve=16 km/s, Dauer 1.5 months.
- power 1000 W, mass 100 kg, Δv=5 km/s, ve=50 km/s, takes 5 months.
Thus ve should notbe too large.
Derivation
Consider the following system:
In the following derivation, „the rocket“ is taken to mean „therocket and all of its unburned propellant“. Newton’s second law ofmotion relates external forces (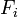 )to the change in linear momentum of the system as follows:
)to the change in linear momentum of the system as follows:
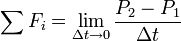
where 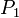 is the momentum of the rocket at time t=0:
is the momentum of the rocket at time t=0:
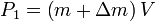
and 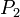 is the momentum of the rocket and exhausted mass at time
is the momentum of the rocket and exhausted mass at time  :
:
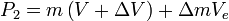
and where, with respect to the observer:
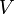 is thevelocity of the rocket at time t=0
is thevelocity of the rocket at time t=0
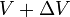 is thevelocity of the rocket at time
is thevelocity of the rocket at time 
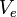 is thevelocity of the mass added to the exhaust (and lost by therocket) during time
is thevelocity of the mass added to the exhaust (and lost by therocket) during time 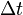
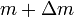 is the massof the rocket at time t=0
is the massof the rocket at time t=0
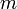 is the massof the rocket at time
is the massof the rocket at time 
The velocity of the exhaust Vein the observer frame is related to the velocity of the exhaust in therocket frame veby
Ve = V − ve
Solving yields:
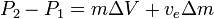
and
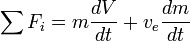
If there are no external forces then 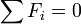 and
and
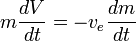
Angenommen, 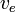 konstant ist, kann dies integriert werden und ergibt:
konstant ist, kann dies integriert werden und ergibt:
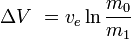
oder äquivalent
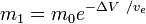 oder
oder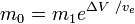
wobei m0 die anfängliche Gesamtmasse einschließlich Treibstoff ist, und m1die endgültige Gesamtmasse und vdie Geschwindigkeit des Raketenausstoßes in Bezug auf die Rakete (der spezifische Impuls oder, falls in Zeit gemessen, dieser multipliziert mit der Erdbeschleunigung).
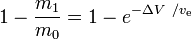 ist der Massenanteil (der Teil der anfänglichen Gesamtmasse, der als Reaktionsmasse ausgegeben wird).
ist der Massenanteil (der Teil der anfänglichen Gesamtmasse, der als Reaktionsmasse ausgegeben wird).
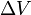 (delta v) ist die Integration über die Zeit der Größe der durch den Einsatz des Raketentriebwerks erzeugten Beschleunigung (was die tatsächliche Beschleunigung wäre, wenn keine äußeren Kräfte vorhanden wären). Im freien Raum ist dies im Falle einer Beschleunigung in Richtung der Geschwindigkeit die Zunahme der Geschwindigkeit. Bei einer Beschleunigung in die entgegengesetzte Richtung (Abbremsung) ist es die Abnahme der Geschwindigkeit.
(delta v) ist die Integration über die Zeit der Größe der durch den Einsatz des Raketentriebwerks erzeugten Beschleunigung (was die tatsächliche Beschleunigung wäre, wenn keine äußeren Kräfte vorhanden wären). Im freien Raum ist dies im Falle einer Beschleunigung in Richtung der Geschwindigkeit die Zunahme der Geschwindigkeit. Bei einer Beschleunigung in die entgegengesetzte Richtung (Abbremsung) ist es die Abnahme der Geschwindigkeit.
Natürlich beschleunigen auch Schwerkraft und Luftwiderstand das Fahrzeug und können zu der vom Fahrzeug erfahrenen Geschwindigkeitsänderung addieren oder subtrahieren.
Delta-v ist daher in der Regel nicht die tatsächliche Geschwindigkeitsänderung des Fahrzeugs.
Obwohl eine extreme Vereinfachung, fasst die Raketengleichung das Wesentliche der Raketenflugphysik in einer einzigen kurzen Gleichung zusammen. Außerdem ist delta-v eine der wichtigsten Größen in der Orbitalmechanik, die angibt, wie schwierig es ist, ein bestimmtes Orbitalmanöver durchzuführen.
Um ein großes delta-v zu erreichen, muss entweder m0 sehr groß sein (exponentiell wachsend, wenn delta-v ansteigt), oder m1 muss winzig sein, oder ve muss sehr hoch sein, oder eine Kombination aus all diesen Faktoren.
In der Praxis wurde dies durch die Verwendung sehr großer Raketen (Erhöhung von m0), mit mehreren Stufen (Verringerung von m1) und Raketen mit sehr hohen Ausstoßgeschwindigkeiten erreicht. Die Saturn-V-Raketen des Apollo-Raumfahrtprogramms und die Ionentriebwerke unbemannter Langstreckensonden sind gute Beispiele dafür.
Die Raketengleichung zeigt eine Art „exponentiellen Zerfall“ der Masse m1, nicht als Funktion der Zeit, sondern als Funktion des erzeugten delta-v. Das Delta-v, das der entsprechenden „Halbwertszeit“ entspricht, ist 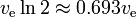
Beispiele
Angenommen, die Ausstoßgeschwindigkeit beträgt 4,5 km/s und Δv 9,7 km/s (von der Erde zum LEO).
- Einstufige Rakete bis zur Umlaufbahn: 1 – e – 9,7 / 4,5= 0,884, also müssen 88,4 % der anfänglichen Gesamtmasse aus Treibstoff bestehen. Die restlichen 11,6 % entfallen auf die Triebwerke, den Tank und die Nutzlast. Im Falle einer Raumfähre würde dies auch den Orbiter einschließen.
- Zwei Stufen bis zur Umlaufbahn: Nehmen wir an, dass die erste Stufe eine Δv von 5,0 km/s liefern soll; 1 – e – 5,0 / 4,5= 0,671, also müssen 67,1 % der anfänglichen Gesamtmasse auf die erste Stufe entfallen. Die verbleibende Masse beträgt 32,9 %. Nach dem Abwurf der ersten Stufe verbleibt eine Masse, die diesen 32 % entspricht.9 %, abzüglich der Masse des Tanks und der Triebwerke der ersten Stufe. Nehmen wir an, dass dies 8 % der ursprünglichen Gesamtmasse sind, dann bleiben 24,9 %. Diese zweite Stufe soll eine Δv von 4,7 km/s liefern; 1 – e – 4,7 / 4,5= 0,648, also müssen 64,8 % der verbleibenden Masse Treibstoff sein, also 16,2 %, und 8,7 % verbleiben für den Tank und die Triebwerke der zweiten Stufe, die Nutzlast und im Falle eines Space Shuttles auch den Orbiter. Insgesamt stehen also 16,7 % für alle Triebwerke, die Tanks, die Nutzlast und den eventuellen Orbiter zur Verfügung.
Anwendbarkeit
Die Raketengleichung gilt für raketenähnliche Reaktionsfahrzeuge, wenn die effektive Abgasgeschwindigkeit konstant ist, und kann summiert oder integriert werden, wenn die effektive Abgasgeschwindigkeit schwankt.
Sie gilt jedoch nicht für andere Technologien wie Kanonenstarts, Weltraumaufzüge, Startschleifen, Fesseltriebwerke und luftatmende Motoren.
Siehe auch
- Delta-v
- Delta-v-Budget
- Oberth-Effekt Die Anwendung von delta-v in a gravitywell increases the final velocity
- Specific impulse
- Spacecraft propulsion
- Mass ratio
- Working mass
- Relativistic rocket
- Reversibility oforbits
|
|
This article includes a list of references, but itssources remain unclear because it has insufficient inline citations. Please help to improvethis article by introducing more precise citations where appropriate. (February2009) |
- ^К. Э. Циолковский, Исследование мировых пространств реактивнымиприборами, 1903. It is available online here in a RARed PDF
- ^ Moore, William; ofthe MilitaryAcademy at Woolwich (1813). A Treatise on the Motion ofRockets. To which is added, An Essay on Naval Gunnery. London: G.and S. Robinson.
- ^ Johnson, W. (1995). „Contents and commentary onWilliam Moore’s a treatise on the motion of rockets and an essay onnaval gunnery“. International Journal of Impact Engineering 16 (3): 499–521. doi:10.1016/0734-743X(94)00052-X. ISSN 0734-743X. http://www.sciencedirect.com/science/article/B6V3K-3Y5FP5P-11/2/c3e98a6cec8f083c93dc4e4e157282bb.
- How to derive the rocket equation
- Relativity Calculator – LearnTsiolkovsky’s rocket equations