| Astrodynamics | ||
| Orbital mechanics | Equations | Efficiencymeasures |
|---|---|---|
| v · d · e |
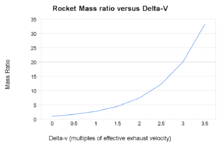
Rocketmassaverhoudingen versus eindsnelheid berekend uit de raketvergelijking
De raketvergelijking van Tsiolkovsky, of ideale raketvergelijking, is een wiskundige vergelijking die de delta-v (de maximale snelheidsverandering van de raket als er geen andere externe krachten werken) in verband brengt met de effectieve uitlaatsnelheid en de begin- en eindmassa van een raket of andere reactiemotor.
De vergelijking is genoemd naar Konstantin Tsiolkovsky die haar onafhankelijk afleidde en publiceerde in zijn werk van 1903. Zij gaat uit van het principe van een raket: een apparaat dat zichzelf kan versnellen (een stuwkracht) door een deel van zijn massa met hoge snelheid in de tegenovergestelde richting uit te stoten ten gevolge van het behoud van momentum.
Voor een dergelijke manoeuvre (of reis die een aantal van dergelijke manoeuvres omvat):
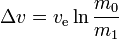
where:
m0 is the initialtotal mass, including propellant. m1 is the finaltotal mass. ve is the effectiveexhaust velocity. (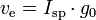 where Isp is the specific impulse expressed as a timeperiod)
where Isp is the specific impulse expressed as a timeperiod)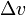 is delta-v-the maximum change of speed of the vehicle (with noexternal forces acting)
is delta-v-the maximum change of speed of the vehicle (with noexternal forces acting)
Units used for mass or velocity do not matter as long as they areconsistent.
- 1 History
- 2 Stages
- 3 Energy
- 4 Derivation
- 5 Examples
- 6 Applicability
- 7 See also
- 8 References
- 9 External links
History
This equation was independently derived by Konstantin Tsiolkovsky towards theend of the 19th century and is widely known under this name and idealrocket equation. Uit een onlangs ontdekt pamflet “A Treatiseon the Motion of Rockets” van William Moores blijkt echter dat de vroegst bekende afleiding van dit soort vergelijking in feite plaatsvond aan de Royal Military Academy te Woolwich in Engeland in 1813, en werd gebruikt voor wapenonderzoek.
Stappen
In het geval van sequentieel stuwende rakettrappen geldt de vergelijking voor elke trap, waarbij voor elke trap de beginmassa in de vergelijking de totale massa van de raket is na het weggooien van de vorige trap, en de eindmassa in de vergelijking de totale massa van de raket is vlak voor het weggooien van de betreffende trap. Voor elke trap kan de specifieke impuls anders zijn.
Bijv. 80% van de massa van een raket is de brandstof van de eerste trap, 10% is de droge massa van de eerste trap, en 10% is de resterende raket, dan
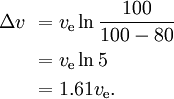 Met drie gelijksoortige, vervolgens kleinere fasen met dezelfde ader voor elke fase, hebben we
Met drie gelijksoortige, vervolgens kleinere fasen met dezelfde ader voor elke fase, hebben we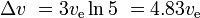
en de nuttige lading is 10%*10%*10% = 0,1% van de oorspronkelijke massa.
Een vergelijkbare SSTO raket, ook met een nuttige lading van 0,1%, zou een massa kunnen hebben van 11% voor brandstoftanks en motoren, en 88,9% voor brandstof. Dat geeft
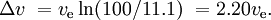
Als de motor van een nieuwe trap wordt ontstoken voordat de vorige trap is weggegooid en de gelijktijdig werkende motoren een verschillende specifieke impuls hebben (zoals vaak het geval is bij vaste-raketboosters en een trap met vloeibare brandstof), is de situatie gecompliceerder.
Energie
In het ideale geval is m1 de nuttige lading en m0 – m1 de reactiemassa (dit komt overeen met lege tanks die geen massa hebben, etc.). De benodigde energie kan eenvoudig worden berekend als
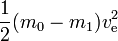
Dit komt overeen met de kinetische energie die de uitgestoten reactiemassa zou hebben bij een snelheid gelijk aan de uitlaatsnelheid. Als de reactiemassa van nul snelheid tot de uitlaatsnelheid zou moeten worden versneld, zou alle geproduceerde energie in de reactiemassa gaan en zou er niets overblijven voor kinetische energiewinst door de raket en de nuttige lading. Als de raket echter al beweegt en versnelt (de reactiemassa wordt uitgestoten in de richting die tegengesteld is aan de richting waarin de raket beweegt) wordt er minder kinetische energie aan de reactiemassa toegevoegd. Als bijvoorbeeld ve=10 km/s en de snelheid van de raket is 3 km/s, dan verandert de snelheid van een kleine hoeveelheid uitgestoten reactiemassa van 3 voorwaarts in 7 km/s achterwaarts. Dus, terwijl de benodigde energie 50 MJ per kg reactiemassa is, wordt slechts 20 MJ gebruikt voor de toename van de snelheid van de reactiemassa. De resterende 30 MJ is de toename van de kinetische energie van de raket en de nuttige lading.
In het algemeen:
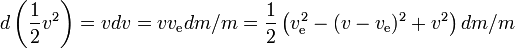
Dus de specifieke energiewinst van de raket in een klein tijdsinterval is de energiewinst van de raket inclusief de resterende brandstof,gedeeld door zijn massa, waarbij de energiewinst gelijk is aan de door de brandstof geproduceerde energie min de energiewinst van de reactiemassa. Hoe groter de snelheid van de raket, hoe kleiner de energiewinst van de reactiemassa; als de snelheid van de raket meer dan de helft is van de uitlaatsnelheid, verliest de reactiemassa zelfs energie bij het uitdrijven, ten voordele van de energiewinst van de raket; hoe groter de snelheid van de raket, hoe groter het energieverlies van de reactiemassa.
We hebben
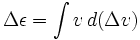
waar ε de specifieke energie van de raket is (potentiële plus kinetische energie) en Δ een aparte variabele is, niet alleen de verandering in v.In het geval dat de raket wordt gebruikt voor vertraging, d.w.z. het uitstoten van reactiemassa in de richting van de snelheid, moet v negatief worden genomen.
De formule is weer voor het ideale geval, waarbij geen energie verloren gaat aan warmte, enz. Dit laatste veroorzaakt een vermindering van de stuwkracht, dus het is een nadeel, zelfs als het doel is energie te verliezen (vertraging).
Als de energie door de massa zelf wordt geproduceerd, zoals in een chemische raket, moet voor de brandstofwaarde 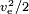 worden genomen, waarbij voor de brandstofwaarde ook de massa van de oxidator in aanmerking moet worden genomen. Een typische waarde is ve= 4,5 km/s, wat overeenkomt met een brandstofwaarde van 10,1 MJ/kg. De werkelijke brandstofwaarde is hoger, maar veel van de energie gaat verloren als afvalwarmte in de uitlaat die de straalpijp niet heeft kunnen onttrekken.
worden genomen, waarbij voor de brandstofwaarde ook de massa van de oxidator in aanmerking moet worden genomen. Een typische waarde is ve= 4,5 km/s, wat overeenkomt met een brandstofwaarde van 10,1 MJ/kg. De werkelijke brandstofwaarde is hoger, maar veel van de energie gaat verloren als afvalwarmte in de uitlaat die de straalpijp niet heeft kunnen onttrekken.
De benodigde energie E is
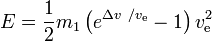
Conclusies:
- voor
 hebben we
hebben we 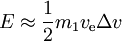
- voor een gegeven Δv is de minimumenergie nodig als ve =0.6275Δv, waarvoor een energie nodig is van
E = 0,772m1(Δv)2. Uitgaande van snelheid nul is dit 54,4 % meer dan alleen de kinetische energie van de lading. In dit optimale geval is de beginmassa 4,92 maal de eindmassa.
Deze resultaten gelden voor een vaste uitlaatsnelheid.
Als gevolg van het Oberth-effect en uitgaande van een niet-zerogene snelheid kan de benodigde potentiële energie van het drijfgas lager zijn dan de toename van de energie in het voertuig en de lading. Dit kan het geval zijn wanneer de reactiemassa na verdrijving een lagere snelheid heeft dan ervoor – raketten zijn in staat om een deel of alle initiële kinetische energie van het stuwmiddel vrij te maken.
Ook kan voor een gegeven doelstelling, zoals van de ene baan naar de andere gaan, de vereiste Δv sterk afhangen van de snelheid waarmee de motor Δv kan produceren en kunnen manoeuvres zelfs onmogelijk zijn als die snelheid te laag is. Bijvoorbeeld, een lancering naar LEO vereist normaal een Δv van ca. 9,5 km/s (vooral voor de snelheid die moet worden verworven), maar als de motor Δv zou kunnen produceren met een snelheid van slechts iets meer dan g, zou het een langzame lancering zijn die in totaal een zeer grote Δv vereist (denk aan zweven zonder enige vooruitgang in snelheid of hoogte te maken, het zou een Δv van 9,8 m/s per seconde kosten). Als de mogelijke snelheid slechts g of minder is, kan de manoeuvre helemaal niet worden uitgevoerd met deze motor.
Het vermogen wordt gegeven door
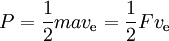
waarbij F de stuwkracht is en a de versnelling die erdoor wordt veroorzaakt. De theoretisch mogelijke stuwkracht per vermogenseenheid is dus 2 gedeeld door de specifieke impuls in m/s. De stuwkrachtefficiëntie is de werkelijke stuwkracht als percentage hiervan.
Als b.v. zonne-energie wordt gebruikt beperkt dit a; in het geval van een grote ve is de mogelijke versnelling omgekeerd evenredig hiermee, vandaar dat de tijd om een vereiste delta-v te bereiken evenredig is met ve; met 100% efficiency:
- voor
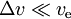 hebben we
hebben we 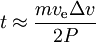
Voorbeelden:
- vermogen 1000 W, massa 100 kg, Δv=5 km/s, ve=16 km/s, duurt 1.5 months.
- power 1000 W, mass 100 kg, Δv=5 km/s, ve=50 km/s, takes 5 months.
Thus ve should notbe too large.
Derivation
Consider the following system:
In the following derivation, “the rocket” is taken to mean “therocket and all of its unburned propellant”. Newton’s second law ofmotion relates external forces (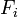 )to the change in linear momentum of the system as follows:
)to the change in linear momentum of the system as follows:
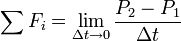
where 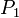 is the momentum of the rocket at time t=0:
is the momentum of the rocket at time t=0:
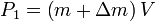
and 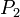 is the momentum of the rocket and exhausted mass at time
is the momentum of the rocket and exhausted mass at time  :
:
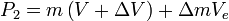
and where, with respect to the observer:
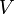 is thevelocity of the rocket at time t=0
is thevelocity of the rocket at time t=0
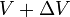 is thevelocity of the rocket at time
is thevelocity of the rocket at time 
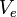 is thevelocity of the mass added to the exhaust (and lost by therocket) during time
is thevelocity of the mass added to the exhaust (and lost by therocket) during time 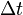
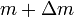 is the massof the rocket at time t=0
is the massof the rocket at time t=0
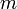 is the massof the rocket at time
is the massof the rocket at time 
The velocity of the exhaust Vein the observer frame is related to the velocity of the exhaust in therocket frame veby
Ve = V − ve
Solving yields:
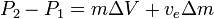
and
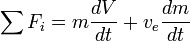
If there are no external forces then 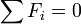 and
and
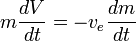
Aannemende dat 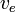 constant is, kan dit worden geïntegreerd om te resulteren in:
constant is, kan dit worden geïntegreerd om te resulteren in:
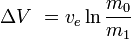
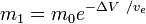 of
of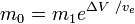
waarin m0 de oorspronkelijke totale massa is, inclusief stuwstof, en m1 de uiteindelijke totale massa en vet de snelheid van de uitlaat van de raket ten opzichte van de raket (de specifieke impuls, of, indien gemeten in tijd, die vermenigvuldigd met de versnelling van de zwaartekracht op aarde).
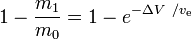 is de massafractie (het deel van de totale oorspronkelijke massa dat als reactiemassa wordt gebruikt).
is de massafractie (het deel van de totale oorspronkelijke massa dat als reactiemassa wordt gebruikt).
Natuurlijk versnellen zwaartekracht en luchtweerstand het voertuig ook, en zij kunnen toevoegen of aftrekken van de verandering in snelheid die het voertuig ondervindt.Vandaar dat delta-v meestal niet de werkelijke verandering in snelheid of snelheid van het voertuig is.
Hoewel het een extreme vereenvoudiging is, vat de raketvergelijking de essentie van raketvluchtfysica in een enkele korte vergelijking. Het is ook zo dat delta-v een van de belangrijkste grootheden is in de baanmechanica, die aangeeft hoe moeilijk het is om een gegeven baanmanoeuvre uit te voeren.
Het is duidelijk dat om een grote delta-v te bereiken, ofwel m0 enorm moet zijn (exponentieel toenemend naarmate delta-v toeneemt), ofwel m1 heel klein moet zijn, ofwel ve heel hoog moet zijn, ofwel een of andere combinatie van dit alles.
In de praktijk is dit bereikt door het gebruik van zeer grote raketten (waardoor m0 toeneemt), met meerdere trappen (waardoor m1 afneemt), en raketten met zeer hoge uitlaatsnelheden. De Saturn Vro-raketten die in het Apollo-ruimtevaartprogramma werden gebruikt en de ion-thrusters die in onbemande lange-afstandssondes worden gebruikt zijn hiervan goede voorbeelden.
De raketvergelijking laat een soort “exponentieel verval” van massa m1 zien, niet als functie van de tijd, maar als functie van de geproduceerde delta-v. De delta-v die de overeenkomstige “halveringstijd” is, is 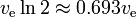
Voorbeelden
Aanname een uitlaatsnelheid van 4.5 km/s en een Δv van 9.7 km/s (Aarde naar LEO).
- Eentrapsraket naar omloopbaan: 1 – e – 9.7 / 4.5= 0.884, dus 88.4 % van de totale initiële massa moet bestaan uit stuwstof. De resterende 11,6 % is voor de motoren, de tank en de lading. In het geval van een spaceshuttle zou dit ook deorbiter omvatten.
- Tweetraps omloopbaan: stel dat de eerste trap een Δv van 5,0 km/s moet leveren; 1 – e – 5,0 / 4,5= 0,671, dus 67,1 % van de totale initiële massa moet stuwstof voor de eerste trap zijn. De resterende massa is 32,9 %. Na verwijdering van de eerste trap blijft er een massa over gelijk aan deze 32.9 %, minus de massa van de tank en de motoren van de eerste trap. Stel dat dit8 % is van de oorspronkelijke totale massa, dan blijft 24,9 % over. Deze tweede trap moet een Δv van 4,7 km/s leveren; 1 – e – 4,7 / 4,5= 0,648, dus 64,8 % van de resterende massa moet stuwstof zijn, dat is 16,2 %, en er blijft 8,7 % over voor de tank en de motoren van de tweede trap, de nuttige lading, en in het geval van een ruimteveer, ook de orbiter. Samen is er dus 16,7 % beschikbaar voor alle motoren, de tanks, de nuttige lading, en de eventuele orbiter.
Toepasbaarheid
De raketvergelijking geldt voor raketachtige reactievoertuigen wanneer de effectieve uitlaatsnelheid constant is; en kan worden opgeteld of geïntegreerd wanneer de effectieve uitlaatsnelheid varieert.
De vergelijking is echter niet van toepassing op andere technologieën, zoals kanonlanceringen, ruimteliften, lanceerlussen, tuibewegingsvoortstuwing en luchtademingsmotoren.
Zie ook
- Delta-v
- Delta-v-budget
- Oberth-effect toepassing van delta-v in a gravitywell increases the final velocity
- Specific impulse
- Spacecraft propulsion
- Mass ratio
- Working mass
- Relativistic rocket
- Reversibility oforbits
|
|
This article includes a list of references, but itssources remain unclear because it has insufficient inline citations. Please help to improvethis article by introducing more precise citations where appropriate. (February2009) |
- ^К. Э. Циолковский, Исследование мировых пространств реактивнымиприборами, 1903. It is available online here in a RARed PDF
- ^ Moore, William; ofthe MilitaryAcademy at Woolwich (1813). A Treatise on the Motion ofRockets. To which is added, An Essay on Naval Gunnery. London: G.and S. Robinson.
- ^ Johnson, W. (1995). “Contents and commentary onWilliam Moore’s a treatise on the motion of rockets and an essay onnaval gunnery”. International Journal of Impact Engineering 16 (3): 499–521. doi:10.1016/0734-743X(94)00052-X. ISSN 0734-743X. http://www.sciencedirect.com/science/article/B6V3K-3Y5FP5P-11/2/c3e98a6cec8f083c93dc4e4e157282bb.
- How to derive the rocket equation
- Relativity Calculator – LearnTsiolkovsky’s rocket equations