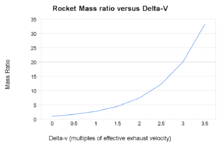
| Astrodynamics | ||
| Orbital mechanics | Equations | Efficiencymeasures |
|---|---|---|
| v · d · e |
チヨルコフスキー式というロケット方程式のこと。 理想ロケット方程式とは、ロケットなどの反応機関の有効排気速度、初期質量、最終質量とデルタv(他に外力が作用しない場合のロケットの最大速度変化)を関係づける数学的な方程式である。
この式は、コンスタンチン・ツィオルコフスキーが独自に導き、1903年の著作で発表したことにちなんで命名されました。
そのような操作 (または、そのような操作をいくつも含む旅) について、以下のように考えてください:
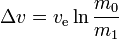
{m_1}
where:
m0 is the initialtotal mass, including propellant. m1 is the finaltotal mass. ve is the effectiveexhaust velocity. (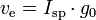 where Isp is the specific impulse expressed as a timeperiod)
where Isp is the specific impulse expressed as a timeperiod)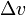 is delta-v-the maximum change of speed of the vehicle (with noexternal forces acting)
is delta-v-the maximum change of speed of the vehicle (with noexternal forces acting)
Units used for mass or velocity do not matter as long as they areconsistent.
- 1 History
- 2 Stages
- 3 Energy
- 4 Derivation
- 5 Examples
- 6 Applicability
- 7 See also
- 8 References
- 9 External links
History
This equation was independently derived by Konstantin Tsiolkovsky towards theend of the 19th century and is widely known under this name and idealrocket equation. しかし、最近発見されたウィリアム・ムーアのパンフレット “A Treatiseon the Motion of Rockets” によると、この種の方程式の最も古い導出は、実は 1813 年にイギリスのウリッジの王立陸軍士官学校で行われ、兵器研究に使用されていたことが分かっている。
ステージ
順次推進するロケットのステージの場合、式はステージごとに適用され、各ステージの式の初期質量は前のステージを破棄した後のロケットの総質量、式の最終質量は該当ステージを破棄する直前のロケットの総質量とします。 比推力は段ごとに異なる場合があります。
例えば、ロケットの質量の80%が1段目の燃料、10%が1段目の乾燥質量、10%が残りのロケットだとすると
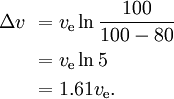
With three similar, subsequently smaller stages with same ve for each stage, wehave
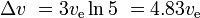 Delta v| = 3 v_text{e}|ln 5| = 4.83 v_text{e}” src=”http://www.neofuel.com/Tsiolkovsky/./index_files/67ff4815a76d7af5afec4a8491a91174.png”>
Delta v| = 3 v_text{e}|ln 5| = 4.83 v_text{e}” src=”http://www.neofuel.com/Tsiolkovsky/./index_files/67ff4815a76d7af5afec4a8491a91174.png”>
そして、ペイロードは初期質量の 10%*10%*10% = 0.1% です。
同様の SSTO ロケットで同じく 0.1% ペイロードの場合、燃料タンクとエンジンで 11%、燃料で 88.9% の質量になる可能性もあります。
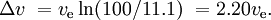
前段を捨てる前に新段のモータを点火し、同時に動作するモータの比推力が異なる場合(固体ロケットブースターや液体燃料段でよくあること)、状況はより複雑になります。 宇宙船の推進力
理想的なケースでは、m1 は有用なペイロード、m0 – m1 は反応質量です (これは、空のタンクには質量がないことなどに相当します)。 必要なエネルギーは、単純に次のように計算できます
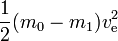 (m_0-m_1)v_text{e}^2
(m_0-m_1)v_text{e}^2
これは、排気速度と同じ速度で、排出される反応質量が持つであろう運動エネルギーに相当します。 もし反応質量がゼロ速度から排気速度まで加速されなければならないとすると、生成されたエネルギーはすべて反応質量に入り、ロケットとペイロードが得る運動エネルギーは何も残らないことになる。 しかし、すでにロケットが動いて加速している場合(ロケットが動く方向と反対方向に反応質量が排出される)、反応質量に加えられる運動エネルギーは少なくなります。 例えば、ve=10km/sでロケットの速度が3km/sの場合、排出された少量の反応物質の速度は、前方の3km/sから後方の7km/sに変化することがわかります。 このように、反応物質1kgあたり50MJのエネルギーが必要ですが、反応物質の速度の増加には20MJしか使われていません。 残りの30MJは、ロケットとペイロードの運動エネルギーの増加分である。
一般に
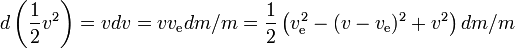
したがって、任意の小さな時間間隔におけるロケットの比エネルギー利得は、残りの燃料を含むロケットのエネルギー利得である。ここで、エネルギー増加は、燃料によって生成されるエネルギーから反応質量によるエネルギー増加を差し引いたものに等しい。 ロケットの速度が大きければ大きいほど、反応物質のエネルギー利得は小さくなります。ロケットの速度が排気速度の半分以上であれば、反応物質は排出される際にエネルギーを失い、ロケットのエネルギー利得の恩恵にあずかりますが、ロケットの速度が大きければ大きいほど、反応物質のエネルギー損失は大きくなります。
以下のようになります。
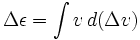
ここでεはロケットの比エネルギー(位置エネルギー+運動エネルギー)、Δvは単なるv変化量ではなく別の変数とします。
この式は、熱などによるエネルギーロスがない、理想的な場合のものである。
化学ロケットのようにエネルギーが質量そのものによって生成される場合、燃料値は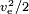 でなければならず、燃料値には酸化剤の質量も考慮されなければならない。 典型的な値はve=4.5km/sで、10.1MJ/kgの燃料値に対応する。 実際の燃料値はもっと高いのですが、エネルギーの多くはノズルが取り出せなかった排気の廃熱として失われています。
でなければならず、燃料値には酸化剤の質量も考慮されなければならない。 典型的な値はve=4.5km/sで、10.1MJ/kgの燃料値に対応する。 実際の燃料値はもっと高いのですが、エネルギーの多くはノズルが取り出せなかった排気の廃熱として失われています。
必要なエネルギーEは
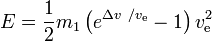
結論です。
- for
 we have
we have 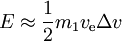
- for a given Δv, the minimumenergy is needed if ve =0.If eltav については、以下のようになる。6275Δvとなり、E=0.772m1(Δv)2のエネルギーが必要となる
。 速度ゼロからのスタートで、これはペイロードの運動エネルギーよりも54.4%多くなっています。 この最適なケースでは、初期質量は最終質量の4.92倍となります。
これらの結果は、排気速度が一定の場合に適用されます。
オバース効果により、速度がゼロでない場合、推進剤から必要な位置エネルギーは、車両と積載物のエネルギー増加分よりも少なくなることがあります。
また、ある軌道から別の軌道に移動するなどの所定の目的について、必要なΔvは、エンジンがΔvを生成できる速度に大きく依存し、その速度が低すぎる場合は、操縦が不可能になることさえあります。 例えば、LEOへの打ち上げには通常約9.5km/sのΔvが必要ですが(主に速度取得のため)、もしエンジンがgより少し大きい程度のΔvしか出せない場合、非常に大きなΔvを必要とする遅い打ち上げになります(速度や高度が全く上がらずホバリングすることを考えると、毎秒9.8mのΔvがかかります)。
動力は次式で与えられる
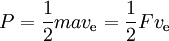
ここでFは推力でaはそれに伴う加速度である。 したがって、理論的に可能な単位出力あたりの推力は、2を比推力(m/s)で割ったものになります。 推力効率とは、実際の推力をこれに対する割合で表したものである。 したがって、必要なΔvに達する時間はveに比例し、100%の効率となります。
- for
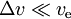 we have
we have 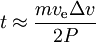
例として、以下のものがあります。
- 電力1000W、質量100kg、Δv=5km/s、ve=16km/s、所要時間1.5 months.
- power 1000 W, mass 100 kg, Δv=5 km/s, ve=50 km/s, takes 5 months.
Thus ve should notbe too large.
Derivation
Consider the following system:
In the following derivation, “the rocket” is taken to mean “therocket and all of its unburned propellant”. Newton’s second law ofmotion relates external forces (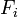 )to the change in linear momentum of the system as follows:
)to the change in linear momentum of the system as follows:
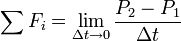
where 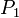 is the momentum of the rocket at time t=0:
is the momentum of the rocket at time t=0:
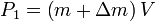
and 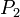 is the momentum of the rocket and exhausted mass at time
is the momentum of the rocket and exhausted mass at time  :
:
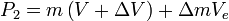
and where, with respect to the observer:
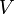 is thevelocity of the rocket at time t=0
is thevelocity of the rocket at time t=0
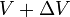 is thevelocity of the rocket at time
is thevelocity of the rocket at time 
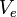 is thevelocity of the mass added to the exhaust (and lost by therocket) during time
is thevelocity of the mass added to the exhaust (and lost by therocket) during time 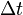
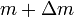 is the massof the rocket at time t=0
is the massof the rocket at time t=0
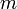 is the massof the rocket at time
is the massof the rocket at time 
The velocity of the exhaust Vein the observer frame is related to the velocity of the exhaust in therocket frame veby
Ve = V − ve
Solving yields:
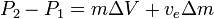
and
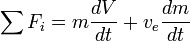
If there are no external forces then 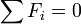 and
and
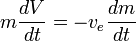
Assuming 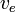 が一定であれば、これを積分して得られる。
が一定であれば、これを積分して得られる。
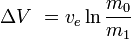 これを積分すると次のようになります。 {m_1}
これを積分すると次のようになります。 {m_1}
あるいは同等に
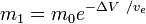 or
or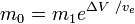
ここでm0は推進剤を含めた初期全質量であります。 m1は最終的な総質量、vはロケットに対する排気の速度(比推力、時間計測の場合は地球上の重力加速度を掛けたもの)です。
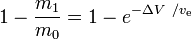 はmassfraction(初期全質量のうち反応質量として費やされる部分)である。
はmassfraction(初期全質量のうち反応質量として費やされる部分)である。
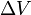 (delta v)は、ロケットエンジンを使ったときの加速度の大きさ(外力がなければ実際の加速度はどの程度か)を時間積分したものである。 自由空間では、速度方向に加速する場合は速度の増加分となる。
(delta v)は、ロケットエンジンを使ったときの加速度の大きさ(外力がなければ実際の加速度はどの程度か)を時間積分したものである。 自由空間では、速度方向に加速する場合は速度の増加分となる。
もちろん重力や抗力も車両を加速させ、車両が受ける速度の変化を加減することができる。
極端に単純化されてはいるが、ロケットの方程式は、ロケットの飛行物理の本質を単一の短い方程式で捉えている。また、Δvは軌道力学で最も重要な量の1つであり、与えられた軌道操縦を行うのがどれほど難しいかを定量化する。
明らかに、大きなΔvを達成するには、m0が巨大(Δv上昇とともに指数的に成長)、またはm1は小さく、または ve は非常に高く、またはこれらすべてのいくつかの組み合わせがなければならない。
実際には、これは、非常に大きなロケット (m0 が増加)、多段 (m1 が減少)、および非常に高い排気速度のロケットの使用によって達成されてきました。
ロケットの方程式は、質量 m1 が時間の関数としてではなく、生成されるデルタ V の関数として、一種の「指数関数的」な減衰を示すものです。 対応する「半減期」である delta-v は 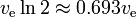
Examples
排気速度が 4.5 km/秒でΔvが 9.7 km/s (Earth to LEO) だと仮定する
- Single stage to orbitrocket:
- 軌道に乗るまでのロケット:1 – e – 9.7 / 4.5= 0.884, したがって、初期の総質量の88.4%は推進剤でなければならない。 残りの11.6%は、エンジン、タンク、ペイロードに充てられます。
- 軌道に乗るための2段階:1段目が5.0km/sのΔvを提供すると仮定すると、1 – e – 5.0 / 4.5= 0.671、したがって最初の総質量の67.1%が1段目への推進剤でなければならない。 残りの質量は32.9%である。 第1段を廃棄した後、この32.9%に相当する質量が残る。9 %から、1段目のタンクとエンジンの質量を差し引いたものです。 これが初期総質量の8 %とすると、24.9 %が残る。 したがって、残りの質量の64.8%は推進剤でなければならず、これは16.2%であり、8.7%は第2段のタンクとエンジン、ペイロード、そしてスペースシャトルの場合はオービターのために残ります。
適用範囲
ロケットの方程式は、有効排気速度が一定であれば、ロケットのような反応物に対して当てはまり、有効排気速度が変化する場合は、合計または積分することができる。
しかし、ガンランチ、宇宙エレベーター、ロンチループ、テザー推進、空気呼吸エンジンなどの他の技術には適用されません。
- Delta-v
- Delta-v budget
- Oberth effect delta-vを適用する効果。v in a gravitywell increases the final velocity
- Specific impulse
- Spacecraft propulsion
- Mass ratio
- Working mass
- Relativistic rocket
- Reversibility oforbits
|
|
This article includes a list of references, but itssources remain unclear because it has insufficient inline citations. Please help to improvethis article by introducing more precise citations where appropriate. (February2009) |
- ^К. Э. Циолковский, Исследование мировых пространств реактивнымиприборами, 1903. It is available online here in a RARed PDF
- ^ Moore, William; ofthe MilitaryAcademy at Woolwich (1813). A Treatise on the Motion ofRockets. To which is added, An Essay on Naval Gunnery. London: G.and S. Robinson.
- ^ Johnson, W. (1995). “Contents and commentary onWilliam Moore’s a treatise on the motion of rockets and an essay onnaval gunnery”. International Journal of Impact Engineering 16 (3): 499–521. doi:10.1016/0734-743X(94)00052-X. ISSN 0734-743X. http://www.sciencedirect.com/science/article/B6V3K-3Y5FP5P-11/2/c3e98a6cec8f083c93dc4e4e157282bb.
- How to derive the rocket equation
- Relativity Calculator – LearnTsiolkovsky’s rocket equations