| Astrodynamics | ||
| Orbital mechanics | Equations | Efficiencymeasures |
|---|---|---|
| v · d · e |
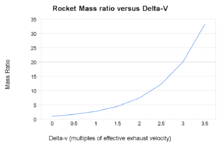
Relación entre la masa del cohete y la velocidad final calculada a partir de la ecuación del cohete
La ecuación del cohete de Tsiolkovsky, o ecuación del cohete ideal, es una ecuación matemática que relaciona el delta-v (el cambio máximo de velocidad del cohete si no actúan otras fuerzas externas) con la velocidad efectiva de escape y la masainicial y final de un cohete u otro motor de reacción.
La ecuación lleva el nombre de KonstantinTsiolkovsky, quien la dedujo y publicó de forma independiente en su obra de 1903.Considera el principio de un cohete:un dispositivo que puede aplicarse a sí mismo una aceleración (un empuje)expulsando parte de su masa con gran velocidad en la dirección opuestadebido a la conservación del momento.
Para cualquier maniobra de este tipo (o viaje que implique varias maniobras de este tipo):
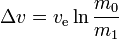
where:
m0 is the initialtotal mass, including propellant. m1 is the finaltotal mass. ve is the effectiveexhaust velocity. (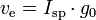 where Isp is the specific impulse expressed as a timeperiod)
where Isp is the specific impulse expressed as a timeperiod)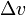 is delta-v-the maximum change of speed of the vehicle (with noexternal forces acting)
is delta-v-the maximum change of speed of the vehicle (with noexternal forces acting)
Units used for mass or velocity do not matter as long as they areconsistent.
- 1 History
- 2 Stages
- 3 Energy
- 4 Derivation
- 5 Examples
- 6 Applicability
- 7 See also
- 8 References
- 9 External links
History
This equation was independently derived by Konstantin Tsiolkovsky towards theend of the 19th century and is widely known under this name and idealrocket equation. Sin embargo, un folleto recientemente descubierto, «A Treatiseon the Motion of Rockets» (Tratado sobre el movimiento de los cohetes), de William Moores, muestra que la primera derivación conocida de este tipo de ecuación se realizó, de hecho, en la Real Academia Militar de Woolwich, en Inglaterra, en 1813, y se utilizó para la investigación de armas.
Etapas
En el caso de las etapas de cohetes de empuje secuencial, la ecuación se aplica a cada etapa, donde para cada etapa la masa inicial en la ecuación es la masa total del cohete después de descartar la etapa anterior, y la masa final en la ecuación es la masa total del cohete justo antes de descartar la etapa en cuestión. Para cada etapa, el impulso específico puede ser diferente.
Por ejemplo, si el 80% de la masa de un cohete es el combustible de la primera etapa, y el 10% es la masa seca de la primera etapa, y el 10% es el cohete restante, entonces
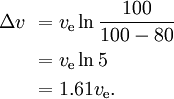 Delta v = v_\text{e} \ln { 100 \over 100 – 80 } {br /> = v_\text{e} \ln 5 \ln = 1.61 v_\text{e}.
Delta v = v_\text{e} \ln { 100 \over 100 – 80 } {br /> = v_\text{e} \ln 5 \ln = 1.61 v_\text{e}.
Con tres etapas similares, posteriormente más pequeñas, con la misma ve para cada etapa, tenemos
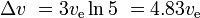
y la carga útil es del 10%*10%*10% = 0,1% de la masa inicial.
Un cohete SSTO comparable, también con una carga útil del 0,1%, podría tener una masa del 11% para los tanques de combustible y los motores, y del 88,9% para el combustible. Esto daría
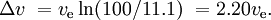
Si el motor de una nueva etapa se enciende antes de que la etapa anterior haya sido desechada y los motores que funcionan simultáneamente tienen un impulso específico diferente (como suele ocurrir con los cohetes impulsores sólidos y la etapa de combustible líquido), la situación es más complicada.
Energía
En el caso ideal m1 es la carga útil y m0 – m1 es la masa de reacción (esto corresponde a que los tanques vacíos no tienen masa, etc.). La energía requerida puede calcularse simplemente como
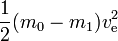
Esto corresponde a la energía cinética que tendría la masa de reacción expulsada a una velocidad igual a la del escape. Si la masa de reacción tuviera que ser acelerada desde la velocidad cero hasta la velocidad de escape, toda la energía producida iría a la masa de reacción y no quedaría nada para la ganancia de energía cinética del cohete y la carga útil. Sin embargo, si el cohete ya se mueve y acelera (la masa de reacción es expulsada en la dirección opuesta a la que se mueve el cohete) se añade menos energía cinética a la masa de reacción. Para ver esto, si, por ejemplo, ve=10 km/s y la velocidad del cohete es de 3 km/s, entonces la velocidad de una pequeña cantidad de masa de reacción expulsada cambia de 3 hacia adelante a 7 km/s hacia atrás. Así, mientras que la energía necesaria es de 50 MJ por kg de masa de reacción, sólo 20 MJ se utilizan para el aumento de la velocidad de la masa de reacción. Los 30 MJ restantes corresponden al aumento de la energía cinética del cohete y de la carga útil.
En general:
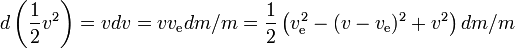
Así, la ganancia de energía específica del cohete en cualquier intervalo de tiempo pequeño es la ganancia de energía del cohete incluyendo el combustible restante,dividido por su masa, donde la ganancia de energía es igual a la energía producida por el combustible menos la ganancia de energía de la masa de reacción. Cuanto mayor sea la velocidad del cohete, menor será la ganancia de energía de la masa de reacción; si la velocidad del cohete es superior a la mitad de la velocidad de escape, la masa de reacción incluso pierde energía al ser expulsada, en beneficio de la ganancia de energía del cohete; cuanto mayor sea la velocidad del cohete, mayor será la pérdida de energía de la masa de reacción.
Tenemos
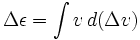
donde ε es la energía específica del cohete (energía potencial más cinética) y Δvis una variable independiente, no sólo el cambio en v.En el caso de utilizar el cohete para la desaceleración, es decir, expulsar la masa de reacción en la dirección de la velocidad, v debe tomarse como negativa.
La fórmula es para el caso ideal de nuevo, sin pérdida de energía en el calor, etc. Esto último provoca una reducción del empuje, por lo que es una ventaja incluso cuando el objetivo es perder energía (desaceleración).
Si la energía es producida por la propia masa, como en un cohete químico, el valor del combustible tiene que ser 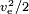 , donde para el valor del combustible también hay que tener en cuenta la masa del oxidante. Un valor típico es ve= 4,5 km/s, que corresponde a un valor de combustible de 10,1 MJ/kg. El valor real del combustible es mayor, pero gran parte de la energía se pierde como calor residual en el escape que la tobera no pudo extraer.
, donde para el valor del combustible también hay que tener en cuenta la masa del oxidante. Un valor típico es ve= 4,5 km/s, que corresponde a un valor de combustible de 10,1 MJ/kg. El valor real del combustible es mayor, pero gran parte de la energía se pierde como calor residual en el escape que la tobera no pudo extraer.
La energía necesaria E es
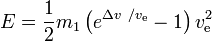
Conclusiones:
- para
 tenemos
tenemos 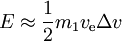
- para un Δv dado, la energía mínima es necesaria si ve =0.6275Δv, requiriendo una energía de
E = 0,772m1(Δv)2. Partiendo de la velocidad cero, esto supone un 54,4 % más que la energía cinética de la carga útil. En este caso óptimo, la masa inicial es 4,92 veces la masa final.
Estos resultados son válidos para una velocidad de escape fija.
Debido al efecto Oberth, y partiendo de una velocidad no nula, la energía potencial necesaria del propulsor puede ser menor que el aumento de energía en el vehículo y la carga útil. Este puede ser el caso cuando la masa de reacción tiene una velocidad más baja después de ser expulsada que antes – los cohetes son capaces de liberar parte o toda la energía cinética inicial del propulsor.
También, para un objetivo dado como moverse de una órbita a otra, la Δv requerida puede depender en gran medida de la tasa a la que el motor puede producir Δv y las maniobras pueden incluso ser imposibles si esa tasa es demasiado baja. Por ejemplo, un lanzamiento a LEO requiere normalmente un Δv de unos 9,5 km/s (sobre todo para adquirir velocidad), pero si el motor pudiera producir Δv a una tasa de sólo un poco más de g, sería un lanzamiento lento que requeriría en conjunto un Δv muy grande (piense en flotar sin hacer ningúnprogreso en velocidad o altitud, costaría un Δvo de 9,8 m/s cada segundo). Si la velocidad posible es sólo g o menos, la maniobra no puede realizarse en absoluto con este motor.
La potencia viene dada por
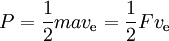
donde F es el empuje y a la aceleración debida al mismo. Así, el empuje teóricamente posible por unidad de potencia es 2 dividido por el impulso específico en m/s. La eficiencia del empuje es el empuje real como porcentaje de éste.
Si, por ejemplo, se utiliza se utiliza la energía solar, esto restringe a; en el caso de una gran ve, la aceleración posible es inversamente proporcional a ella, por lo que el tiempo para alcanzar una delta-v requerida es proporcional a ve; con una eficiencia del 100%:
- para
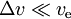 tenemos
tenemos 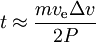
Ejemplos:
- Potencia 1000 W, masa 100 kg, Δv=5 km/s, ve=16 km/s, tarda 1.5 months.
- power 1000 W, mass 100 kg, Δv=5 km/s, ve=50 km/s, takes 5 months.
Thus ve should notbe too large.
Derivation
Consider the following system:
In the following derivation, «the rocket» is taken to mean «therocket and all of its unburned propellant». Newton’s second law ofmotion relates external forces (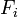 )to the change in linear momentum of the system as follows:
)to the change in linear momentum of the system as follows:
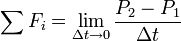
where 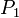 is the momentum of the rocket at time t=0:
is the momentum of the rocket at time t=0:
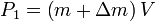
and 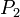 is the momentum of the rocket and exhausted mass at time
is the momentum of the rocket and exhausted mass at time  :
:
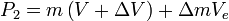
and where, with respect to the observer:
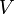 is thevelocity of the rocket at time t=0
is thevelocity of the rocket at time t=0
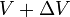 is thevelocity of the rocket at time
is thevelocity of the rocket at time 
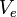 is thevelocity of the mass added to the exhaust (and lost by therocket) during time
is thevelocity of the mass added to the exhaust (and lost by therocket) during time 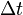
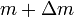 is the massof the rocket at time t=0
is the massof the rocket at time t=0
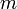 is the massof the rocket at time
is the massof the rocket at time 
The velocity of the exhaust Vein the observer frame is related to the velocity of the exhaust in therocket frame veby
Ve = V − ve
Solving yields:
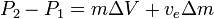
and
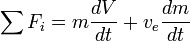
If there are no external forces then 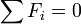 and
and
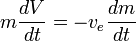
Suponiendo que 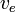 es constante, esto se puede integrar para obtener:
es constante, esto se puede integrar para obtener:
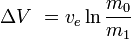
o, de forma equivalente
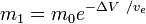 o
o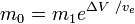
donde m0 es la masa total inicial incluyendo el propulsor, y m1la masa total final y vla velocidad del escape del cohete con respecto al cohete (el impulso específico, o, si se mide en tiempo, el multiplicado por la aceleración de la gravedad en la Tierra).
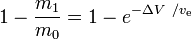 es la fracción de masa (la parte de la masa total inicial que se gasta como masa de reacción).
es la fracción de masa (la parte de la masa total inicial que se gasta como masa de reacción).
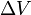 (delta v) es la integración en el tiempo de la magnitud de la aceleración producida por el uso del motor del cohete (lo que sería la aceleración real si no hubiera fuerzas externas). En el espacio libre, para el caso de la aceleración en la dirección de la velocidad, es el aumento de la velocidad. En el caso de una aceleración en la dirección opuesta (desaceleración), es la disminución de la velocidad.
(delta v) es la integración en el tiempo de la magnitud de la aceleración producida por el uso del motor del cohete (lo que sería la aceleración real si no hubiera fuerzas externas). En el espacio libre, para el caso de la aceleración en la dirección de la velocidad, es el aumento de la velocidad. En el caso de una aceleración en la dirección opuesta (desaceleración), es la disminución de la velocidad.
Por supuesto, la gravedad y la resistencia también aceleran el vehículo, y pueden sumar o restar al cambio de velocidad que experimenta el vehículo.Por lo tanto, delta-v no suele ser el cambio real de la velocidad del vehículo.
Aunque se trata de una simplificación extrema, la ecuación del cohete capta lo esencial de la física del vuelo de los cohetes en una sola ecuación corta. También sucede que delta-v es una de las cantidades más importantes en la mecánica orbital, que cuantifica lo difícil que es realizar una determinada maniobra orbital.
Claramente, para lograr un gran delta-v, o bien m0 debe ser enorme (creciendo exponencialmente a medida que el delta-v aumenta), o m1 debe ser diminuto, o ve debe ser muy alto, o alguna combinación de todos ellos.
En la práctica, esto se ha conseguido utilizando cohetes muy grandes (aumentando m0), con múltiples etapas (disminuyendo m1), y cohetes con velocidades de escape muy altas. Los cohetes Saturno V utilizados en el programa espacial Apolo y los propulsores iónicos utilizados en las sondas no tripuladas de larga distancia son buenos ejemplos de ello.
La ecuación de los cohetes muestra una especie de «decaimiento exponencial» de la masa m1, no en función del tiempo, sino en función de la delta-v producida. El delta-v que es la «vida media» correspondiente es 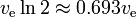
Ejemplos
Supongamos una velocidad de escape de 4,5 km/s y un Δv de 9,7 km/s (Tierra a LEO).
- Cohete de una etapa a órbita: 1 – e – 9,7 / 4,5= 0,884, por lo que el 88,4 % de la masa total inicial tiene que ser propulsor. El 11,6% restante es para los motores, el tanque y la carga útil. En el caso de un transbordador espacial, también incluiría el orbitador.
- Dos etapas hasta la órbita: supongamos que la primera etapa debe proporcionar un Δvo de 5,0 km/s; 1 – e – 5,0 / 4,5= 0,671, por lo que el 67,1% de la masa total inicial tiene que ser propulsor de la primera etapa. La masa restante es del 32,9%. Tras la eliminación de la primera etapa, queda una masa igual a este 32.9 %, menos la masa del tanque y los motores de la primera etapa. Supongamos que se trata de un 8% de la masa total inicial, entonces queda un 24,9%. Esta segunda etapa debe proporcionar un Δvo de 4,7 km/s; 1 – e – 4,7 / 4,5= 0,648, por lo que el 64,8% de la masa restante tiene que ser propulsor, que es el 16,2%, y el 8,7% queda para el tanque y los motores de la segunda etapa, la carga útil y, en el caso de un transbordador espacial, también el orbitador. Por lo tanto, el 16,7 % está disponible para todos los motores, los tanques, la carga útil y el posible orbitador.
- Delta-v
- Presupuesto delta-v
- Efecto Oberth aplicando delta-v in a gravitywell increases the final velocity
- Specific impulse
- Spacecraft propulsion
- Mass ratio
- Working mass
- Relativistic rocket
- Reversibility oforbits
- ^К. Э. Циолковский, Исследование мировых пространств реактивнымиприборами, 1903. It is available online here in a RARed PDF
- ^ Moore, William; ofthe MilitaryAcademy at Woolwich (1813). A Treatise on the Motion ofRockets. To which is added, An Essay on Naval Gunnery. London: G.and S. Robinson.
- ^ Johnson, W. (1995). «Contents and commentary onWilliam Moore’s a treatise on the motion of rockets and an essay onnaval gunnery». International Journal of Impact Engineering 16 (3): 499–521. doi:10.1016/0734-743X(94)00052-X. ISSN 0734-743X. http://www.sciencedirect.com/science/article/B6V3K-3Y5FP5P-11/2/c3e98a6cec8f083c93dc4e4e157282bb.
- How to derive the rocket equation
- Relativity Calculator – LearnTsiolkovsky’s rocket equations
Aplicabilidad
La ecuación del cohete es válida para los vehículos de reacción tipo cohete siempre que la velocidad efectiva de escape sea constante; y puede sumarse o integrarse cuando la velocidad efectiva de escape varía.
Sin embargo, no se aplica a otras tecnologías como los lanzamientos de cañones, los ascensores espaciales, los bucles de lanzamiento, la propulsión de anclaje y los motores de respiración de aire.
Ver también
|
|
This article includes a list of references, but itssources remain unclear because it has insufficient inline citations. Please help to improvethis article by introducing more precise citations where appropriate. (February2009) |