Durante los últimos días, el mundo de las matemáticas ha estado en plena efervescencia por la noticia de que Sir Michael Atiyah, el famoso medallista Fields y ganador del premio Abel, afirma haber resuelto la hipótesis de Riemann.
Si su demostración resulta ser correcta, sería uno de los logros matemáticos más importantes en muchos años. De hecho, sería uno de los mayores resultados en matemáticas, comparable a la demostración del Último Teorema de Fermat de 1994 y a la demostración de la Conjetura de Poincare de 2002.
Además de ser uno de los grandes problemas no resueltos de las matemáticas y, por tanto, de cosechar la gloria para quien lo resuelva, la hipótesis de Riemann es uno de los «Problemas del millón de dólares» del Instituto Clay de Matemáticas. Sin duda, una solución supondría un botín bastante rentable: un millón de dólares.
La hipótesis de Riemann tiene que ver con la distribución de los números primos, esos enteros que sólo se pueden dividir por sí mismos y por uno, como el 3, el 5, el 7, el 11, etc. Sabemos por los griegos que hay infinitos números primos. Lo que no sabemos es cómo se distribuyen dentro de los enteros.
El problema tiene su origen en la estimación de la llamada función «pi primo», una ecuación para encontrar el número de primos menores que un número dado. Pero su reformulación moderna, realizada por el matemático alemán Bernhard Riemann en 1858, tiene que ver con la localización de los ceros de lo que hoy se conoce como la función zeta de Riemann.
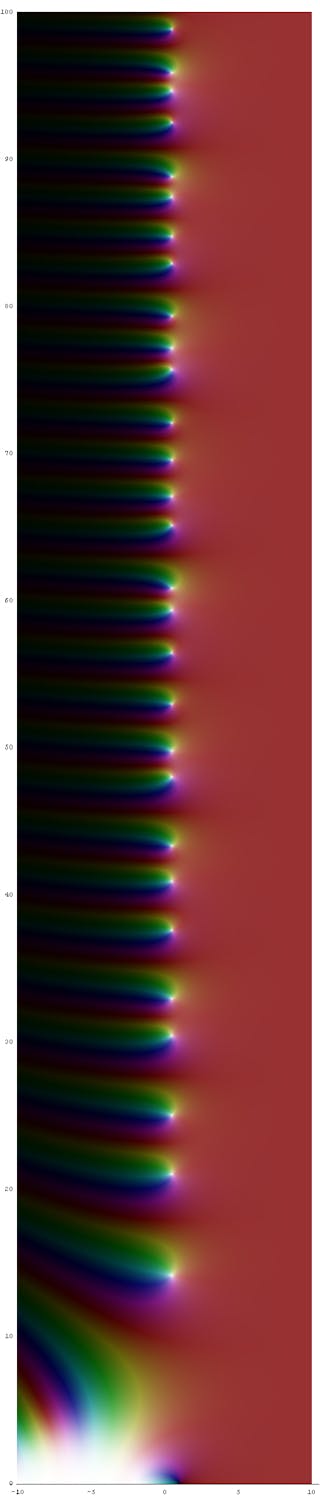
El enunciado técnico de la hipótesis de Riemann es «los ceros de la función zeta de Riemann que están en la franja crítica deben estar en la línea crítica». Incluso la comprensión de ese enunciado implica cursos de matemáticas de posgrado en análisis complejo.
La mayoría de los matemáticos creen que la hipótesis de Riemann es efectivamente cierta. Los cálculos realizados hasta ahora no han arrojado ningún cero que se comporte mal y que no se encuentre en la línea crítica. Sin embargo, hay infinitos de estos ceros para comprobar, por lo que un cálculo por ordenador no verificará tanto. Sólo una prueba abstracta servirá.
Si, de hecho, la hipótesis de Riemann no fuera cierta, el pensamiento actual de los matemáticos sobre la distribución de los números primos estaría muy equivocado, y tendríamos que replantearnos seriamente los primos.
La hipótesis de Riemann ha sido examinada durante más de un siglo y medio por algunos de los más grandes nombres de las matemáticas y no es el tipo de problema con el que un estudiante de matemáticas sin experiencia pueda jugar en su tiempo libre. Los intentos de verificarlo implican muchas herramientas muy profundas del análisis complejo y suelen ser muy serios realizados por algunos de los mejores nombres de las matemáticas.
Atiyah dio una conferencia en Alemania el 25 de septiembre en la que presentó un esquema de su enfoque para verificar la hipótesis de Riemann. Este esbozo suele ser el primer anuncio de la solución, pero no debe tomarse como que el problema está resuelto, ni mucho menos. Para los matemáticos como yo, la «prueba está en el pudín», y hay muchos pasos que deben darse antes de que la comunidad pronuncie la solución de Atiyah como correcta. En primer lugar, tendrá que hacer circular un manuscrito que detalle su solución. A continuación, está la minuciosa tarea de verificar su prueba. Esto podría llevar bastante tiempo, tal vez meses o incluso años.
¿Es serio el intento de Atiyah sobre la hipótesis de Riemann? Tal vez. Su reputación es estelar, y sin duda es lo suficientemente capaz como para llevarlo a cabo. Por otro lado, ha habido otros intentos serios de resolver este problema que no han dado resultado. En algún momento, Atiyah tendrá que hacer circular un manuscrito que los expertos puedan revisar con un peine de dientes finos.