Ces derniers jours, le monde des mathématiques s’est enflammé à la nouvelle que Sir Michael Atiyah, le célèbre médaillé Fields et lauréat du prix Abel, prétend avoir résolu l’hypothèse de Riemann.
Si sa preuve s’avère correcte, ce serait l’une des plus importantes réalisations mathématiques depuis de nombreuses années. En fait, ce serait l’un des plus grands résultats en mathématiques, comparable à la preuve du dernier théorème de Fermat de 1994 et à la preuve de la conjecture de Poincaré de 2002.
En plus d’être l’un des grands problèmes non résolus des mathématiques et donc de garnir la gloire de celui qui le résout, l’hypothèse de Riemann est l’un des « Million Dollar Problems » du Clay Mathematics Institute. » Une solution donnerait certainement un butin assez rentable : un million de dollars.
L’hypothèse de Riemann a trait à la distribution des nombres premiers, ces entiers qui ne peuvent être divisés que par eux-mêmes et un, comme 3, 5, 7, 11 et ainsi de suite. Les Grecs nous ont appris qu’il existe une infinité de nombres premiers. Ce que nous ne savons pas, c’est comment ils sont répartis au sein des nombres entiers.
Le problème trouve son origine dans l’estimation de la fonction dite « prime pi », une équation permettant de trouver le nombre de nombres premiers inférieurs à un nombre donné. Mais sa reformulation moderne, par le mathématicien allemand Bernhard Riemann en 1858, a trait à l’emplacement des zéros de ce que l’on appelle aujourd’hui la fonction zêta de Riemann.
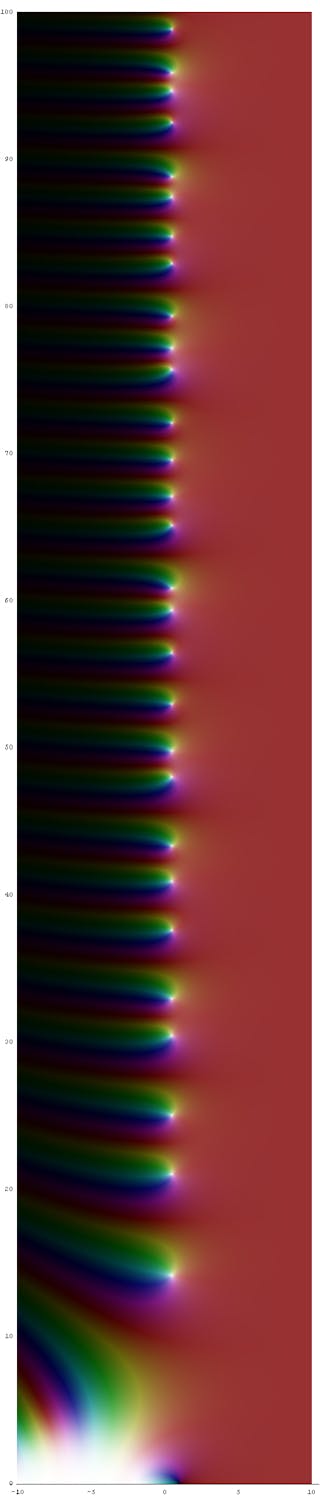
L’énoncé technique de l’hypothèse de Riemann est « les zéros de la fonction zêta de Riemann qui se trouvent dans la bande critique doivent se trouver sur la ligne critique. » Même la compréhension de cet énoncé implique des cours de mathématiques de niveau supérieur en analyse complexe.
La plupart des mathématiciens pensent que l’hypothèse de Riemann est effectivement vraie. Les calculs effectués jusqu’à présent n’ont pas donné de zéros malencontreux qui ne se trouvent pas sur la ligne critique. Cependant, il y a une infinité de ces zéros à vérifier, et donc un calcul informatique ne vérifiera pas grand-chose. Seule une preuve abstraite fera l’affaire.
Si, en fait, l’hypothèse de Riemann n’était pas vraie, alors la pensée actuelle des mathématiciens sur la distribution des nombres premiers serait très éloignée, et nous devrions sérieusement repenser les nombres premiers.
L’hypothèse de Riemann est examinée depuis plus d’un siècle et demi par certains des plus grands noms des mathématiques et n’est pas le genre de problème avec lequel un étudiant en mathématiques inexpérimenté peut s’amuser pendant son temps libre. Les tentatives de vérification impliquent de nombreux outils très profonds issus de l’analyse complexe et sont généralement très sérieuses réalisées par certains des plus grands noms des mathématiques.
Atiyah a donné une conférence en Allemagne le 25 septembre dans laquelle il a présenté un aperçu de son approche pour vérifier l’hypothèse de Riemann. Cette esquisse est souvent la première annonce de la solution mais il ne faut pas croire que le problème est résolu, loin de là. Pour les mathématiciens comme moi, « c’est à l’usage que l’on trouve la preuve », et de nombreuses étapes doivent être franchies avant que la communauté ne déclare que la solution d’Atiyah est correcte. Tout d’abord, il devra faire circuler un manuscrit détaillant sa solution. Ensuite, il y a la tâche minutieuse de la vérification de sa preuve. Cela pourrait prendre pas mal de temps, peut-être des mois ou même des années.
La tentative d’Atiyah sur l’hypothèse de Riemann est-elle sérieuse ? Peut-être. Sa réputation est stellaire, et il est certainement assez capable pour y parvenir. D’un autre côté, il y a eu plusieurs autres tentatives sérieuses sur ce problème qui n’ont pas abouti. À un moment donné, Atiyah devra faire circuler un manuscrit que les experts pourront vérifier au peigne fin.