Az elmúlt napokban a matematika világa attól a hírtől volt hangos, hogy Sir Michael Atiyah, a híres Fields-érmes és Abel-díjas matematikus azt állítja, hogy megoldotta a Riemann-hipotézist.
Ha bizonyítása helyesnek bizonyul, ez hosszú évek óta az egyik legfontosabb matematikai eredmény lenne. Valójában ez lenne az egyik legnagyobb eredmény a matematikában, összehasonlítható a Fermat utolsó tételének 1994-es bizonyításával és a Poincare-sejtés 2002-es bizonyításával.
Amellett, hogy a Riemann-hipotézis a matematika egyik nagy megoldatlan problémája, és ezért dicsőséget szerez annak, aki megoldja, a Clay Matematikai Intézet egyik “Millió dolláros problémája”. Megoldása minden bizonnyal igen jövedelmező zsákmányt eredményezne: egymillió dollárt.
A Riemann-hipotézis a prímszámok eloszlásával kapcsolatos, azokkal az egész számokkal, amelyek csak önmagukkal és eggyel oszthatók, például 3, 5, 7, 11 és így tovább. A görögöktől tudjuk, hogy végtelen sok prímszám van. Azt viszont nem tudjuk, hogy ezek hogyan oszlanak meg az egész számok között.
A probléma az úgynevezett “prím pi” függvény becsléséből ered, amely egy egyenlet egy adott számnál kisebb prímszámok számának meghatározására. Modern újrafogalmazása azonban Bernhard Riemann német matematikus által 1858-ban történt, és a ma Riemann-zéta-függvényként ismert zérusainak helyével kapcsolatos.
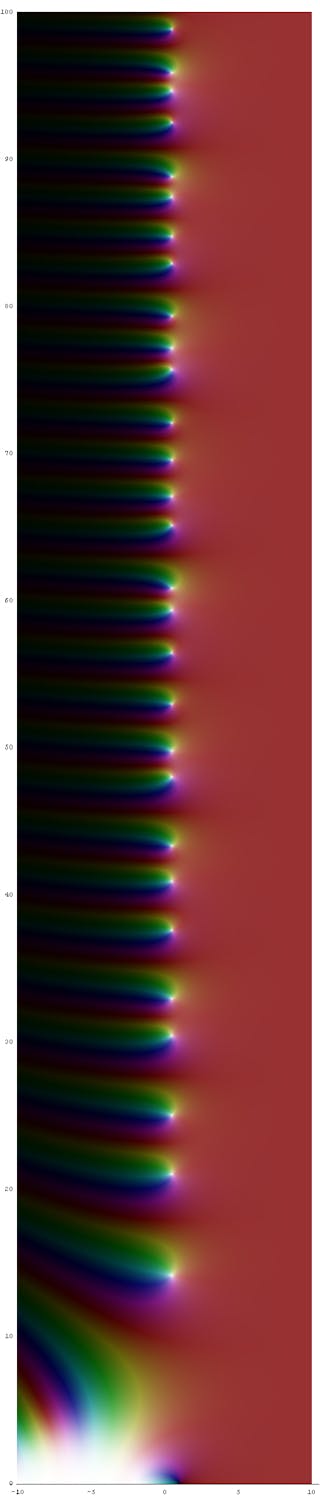
A Riemann-hipotézis technikai megfogalmazása a következő: “a Riemann-zétafüggvény azon zérusainak, amelyek a kritikus sávban vannak, a kritikus egyenesre kell esniük”. Még ennek az állításnak a megértéséhez is szükségesek a komplex analízis felsőfokú matematika kurzusok.
A legtöbb matematikus úgy véli, hogy a Riemann-hipotézis valóban igaz. Az eddigi számítások nem mutattak ki olyan rosszul viselkedő zérusokat, amelyek nem a kritikus egyenesben feküdnének. Azonban végtelenül sok ilyen nullpontot kell ellenőrizni, így egy számítógépes számítással nem sok mindent lehet igazolni. Csak egy absztrakt bizonyítás lesz elegendő.
Ha a Riemann-hipotézis valójában nem lenne igaz, akkor a matematikusok jelenlegi gondolkodásmódja a prímszámok eloszlásáról messze elrugaszkodna, és komolyan újra kellene gondolnunk a prímszámokat.
A Riemann-hipotézist több mint másfél évszázada vizsgálják a matematika legnagyobbjai, és nem az a fajta probléma, amellyel egy tapasztalatlan matematikatanuló a szabadidejében eljátszadozhat. Az ellenőrzésére tett kísérletek a komplex analízis számos, nagyon mélyreható eszközét foglalják magukban, és általában nagyon komoly kísérleteket tesznek a matematika legnagyobb nevei.
Atiyah szeptember 25-én Németországban tartott egy előadást, amelyben vázlatosan bemutatta a Riemann-hipotézis ellenőrzésére irányuló megközelítését. Ez a vázlat gyakran a megoldás első bejelentése, de nem szabad úgy venni, hogy a probléma megoldódott – távolról sem. A hozzám hasonló matematikusok számára a “bizonyíték a pudingban van”, és még sok lépésnek kell megtörténnie ahhoz, hogy a közösség helyesnek nyilvánítsa Atiyah megoldását. Először is körbe kell adnia egy kéziratot, amelyben részletesen leírja a megoldását. Ezután következik a bizonyítás ellenőrzésének fáradságos feladata. Ez elég sok időt vehet igénybe, talán hónapokat vagy akár éveket is.
Atiyah kísérlete a Riemann-hipotézisre komolyan vehető? Talán igen. A hírneve kiváló, és minden bizonnyal elég alkalmas ahhoz, hogy véghezvigye. Másrészt, több más komoly kísérlet is volt már erre a problémára, amelyek nem jártak sikerrel. Valamikor Atiyah-nak egy olyan kéziratot kell majd köröztetnie, amelyet a szakértők finom fésűvel ellenőrizhetnek.