Negli ultimi giorni, il mondo della matematica è stato in fermento per la notizia che Sir Michael Atiyah, il famoso medaglia Fields e vincitore del premio Abel, sostiene di aver risolto l’ipotesi di Riemann.
Se la sua dimostrazione si rivelasse corretta, questo sarebbe uno dei risultati matematici più importanti degli ultimi anni. In effetti, sarebbe uno dei più grandi risultati in matematica, paragonabile alla dimostrazione dell’Ultimo Teorema di Fermat del 1994 e alla dimostrazione della Congettura di Poincare del 2002.
Oltre ad essere uno dei grandi problemi irrisolti della matematica e quindi a procurare gloria a chi lo risolve, l’ipotesi di Riemann è uno dei “Million Dollar Problems” del Clay Mathematics Institute. Una sua soluzione frutterebbe certamente un bottino piuttosto redditizio: un milione di dollari.
L’ipotesi di Riemann ha a che fare con la distribuzione dei numeri primi, quei numeri interi che possono essere divisi solo per se stessi e uno, come 3, 5, 7, 11 e così via. Sappiamo dai greci che ci sono infiniti numeri primi. Quello che non sappiamo è come sono distribuiti all’interno dei numeri interi.
Il problema ha avuto origine nella stima della cosiddetta funzione “pi greco primo”, un’equazione per trovare il numero di primi inferiori a un dato numero. Ma la sua riformulazione moderna, ad opera del matematico tedesco Bernhard Riemann nel 1858, ha a che fare con la posizione degli zeri di quella che oggi è nota come funzione zeta di Riemann.
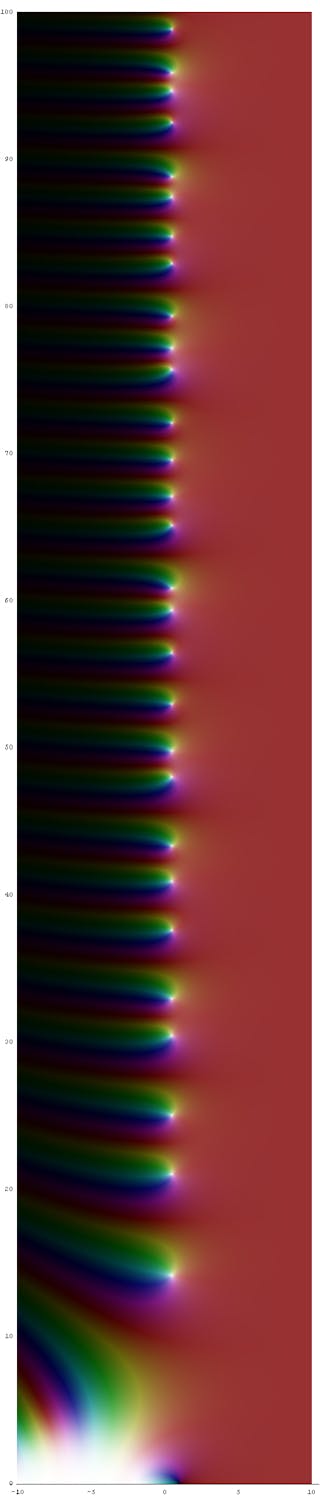
L’affermazione tecnica dell’ipotesi di Riemann è “gli zeri della funzione zeta di Riemann che si trovano nella fascia critica devono trovarsi sulla linea critica”. Anche la comprensione di questa affermazione implica corsi di matematica a livello di laurea in analisi complessa.
La maggior parte dei matematici crede che l’ipotesi di Riemann sia effettivamente vera. I calcoli effettuati finora non hanno prodotto alcuno zero errato che non si trovi nella linea critica. Tuttavia, ci sono infiniti di questi zeri da controllare, e quindi un calcolo al computer non potrà verificare tutto questo. Solo una prova astratta lo farà.
Se, infatti, l’ipotesi di Riemann non fosse vera, allora l’attuale pensiero dei matematici sulla distribuzione dei numeri primi sarebbe fuori strada, e avremmo bisogno di ripensare seriamente i primi.
L’ipotesi di Riemann è stata esaminata per oltre un secolo e mezzo da alcuni dei più grandi nomi della matematica e non è il tipo di problema con cui uno studente di matematica inesperto può giocare nel suo tempo libero. I tentativi di verificarlo coinvolgono molti strumenti molto profondi dell’analisi complessa e sono di solito molto seri fatti da alcuni dei migliori nomi della matematica.
Atiyah ha tenuto una conferenza in Germania il 25 settembre in cui ha presentato uno schema del suo approccio per verificare l’ipotesi di Riemann. Questo schema è spesso il primo annuncio della soluzione, ma non si deve pensare che il problema sia stato risolto – tutt’altro. Per i matematici come me, la “prova è nel budino”, e ci sono molti passi che devono essere fatti prima che la comunità dichiari la soluzione di Atiyah come corretta. Per prima cosa, dovrà far circolare un manoscritto che dettaglia la sua soluzione. Poi, c’è il compito certosino di verificare la sua prova. Questo potrebbe richiedere molto tempo, forse mesi o addirittura anni.
Il tentativo di Atiyah sull’ipotesi Riemann è serio? Può darsi. La sua reputazione è stellare, e lui è certamente abbastanza capace da riuscirci. D’altra parte, ci sono stati diversi altri tentativi seri su questo problema che non hanno avuto successo. Ad un certo punto, Atiyah dovrà far circolare un manoscritto che gli esperti possano controllare con un pettine a denti stretti.