| Astrodynamics | ||
| Orbital mechanics | Equations | Efficiencymeasures |
|---|---|---|
| v · d · e |
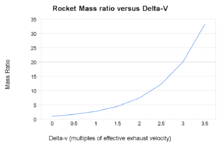
Współczynniki masy rakiety w stosunku do prędkości końcowej obliczone z równania rakietowego
Równanie rakietowe Tsiolkovsky’ego, lub idealne równanie rakietowe, jest równaniem matematycznym, które odnosi delta-v (maksymalną zmianę prędkości rakiety, jeśli nie działają inne siły zewnętrzne) do efektywnej prędkości wylotowej oraz początkowej i końcowej masy rakiety lub innego silnika reakcyjnego.
Równanie zostało nazwane na cześć Konstantego Ciołkowskiego, który samodzielnie je wyprowadził i opublikował w swojej pracy z 1903 r. Uwzględnia ono zasadę działania rakiety: urządzenia, które może nadać sobie przyspieszenie (ciąg) poprzez wyrzucenie części swojej masy z dużą prędkością w przeciwnym kierunku, dzięki zachowaniu pędu.
Dla każdego takiego manewru (lub podróży składającej się z wielu takich manewrów):
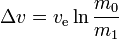
where:
m0 is the initialtotal mass, including propellant. m1 is the finaltotal mass. ve is the effectiveexhaust velocity. (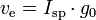 where Isp is the specific impulse expressed as a timeperiod)
where Isp is the specific impulse expressed as a timeperiod)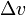 is delta-v-the maximum change of speed of the vehicle (with noexternal forces acting)
is delta-v-the maximum change of speed of the vehicle (with noexternal forces acting)
Units used for mass or velocity do not matter as long as they areconsistent.
- 1 History
- 2 Stages
- 3 Energy
- 4 Derivation
- 5 Examples
- 6 Applicability
- 7 See also
- 8 References
- 9 External links
History
This equation was independently derived by Konstantin Tsiolkovsky towards theend of the 19th century and is widely known under this name and idealrocket equation. Jednak niedawno odkryta broszura „A Treatiseon the Motion of Rockets” autorstwa Williama Mooresh’a pokazuje, że najwcześniejsze znane wyprowadzenie tego rodzaju równania miało miejsce w Królewskiej Akademii Wojskowej woolwich w Anglii w 1813 roku i było wykorzystywane do badań nad bronią.
Etapy
W przypadku kolejnych stopni rakiety, równanie stosuje się do każdego etapu, gdzie dla każdego etapu masa początkowa w równaniu jest całkowitą masą rakiety po odrzuceniu poprzedniego etapu, a masa końcowa w równaniu jest całkowitą masą rakiety tuż przed odrzuceniem danego etapu. Dla każdego etapu impuls właściwy może być inny.
Na przykład, jeżeli 80% masy rakiety to paliwo pierwszego stopnia, a 10% to sucha masa pierwszego stopnia, a 10% to pozostała masa rakiety, to
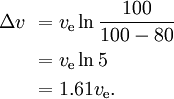
Przy trzech podobnych, następnie mniejszych etapach z tym samym ve dla każdego etapu, mamy
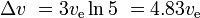
a ładunek użyteczny wynosi 10%*10%*10% = 0,1% masy początkowej.
Porównywalna rakieta SSTO, również o ładunku użytecznym 0,1%, mogłaby mieć masę 11% dla zbiorników paliwa i silników oraz 88,9% dla paliwa. Dałoby to
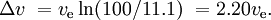
Jeśli silnik nowego stopnia jest zapalany przed odrzuceniem poprzedniego stopnia, a jednocześnie pracujące silniki mają różne impulsy właściwe (jak to często ma miejsce w przypadku stałych boosterów rakietowych i stopni na paliwo ciekłe), sytuacja jest bardziej skomplikowana.
Energia
W idealnym przypadku m1 to ładunek użyteczny, a m0 – m1 to masa reakcyjna (odpowiada to pustym zbiornikom nie posiadającym masy, itd.). Wymaganą energię można po prostu obliczyć jako
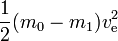
Odpowiada to energii kinetycznej, jaką miałaby wyrzucona masa reakcyjna przy prędkości równej prędkości wylotowej. Jeżeli masa reakcyjna musiałaby zostać rozpędzona od prędkości zerowej do prędkości wylotowej, cała wytworzona energia zostałaby skierowana do masy reakcyjnej i nic nie pozostałoby na zyskanie energii kinetycznej przez rakietę i ładunek użyteczny. Jednakże, jeżeli rakieta już się porusza i przyspiesza (masa reakcyjna jest wyrzucana w kierunku przeciwnym do kierunku, w którym porusza się rakieta), mniej energii kinetycznej jest dodawane do masy reakcyjnej. Aby to zobaczyć, jeśli na przykład ve=10 km/s i prędkość rakiety wynosi 3 km/s, wtedy prędkość niewielkiej ilości wyrzuconej masy reakcyjnej zmienia się z 3 do przodu na 7 km/s do tyłu. Tak więc, podczas gdy wymagana energia wynosi 50 MJ na kg masy reakcyjnej, tylko 20 MJ jest zużywane na wzrost prędkości masy reakcyjnej. Pozostałe 30 MJ to wzrost energii kinetycznej rakiety i ładunku.
Ogólnie:
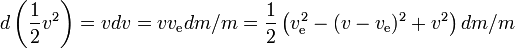
Tak więc przyrost energii rakiety w dowolnym małym przedziale czasu jest przyrostem energii rakiety z uwzględnieniem pozostałego paliwa,podzielony przez jej masę, gdzie przyrost energii jest równy energii wytwarzanej przez paliwo minus przyrost energii masy reakcyjnej. Im większa prędkość rakiety, tym mniejszy przyrost energii masy reakcyjnej; jeżeli prędkość rakiety jest większa niż połowa prędkości wylotowej, masa reakcyjna traci nawet energię przy wyrzucaniu, na korzyść przyrostu energii rakiety; im większa prędkość rakiety, tym większa strata energii masy reakcyjnej.
Mamy
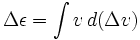
gdzie ε jest specyficzną energią rakiety (energia potencjalna plus energia kinetyczna) i Δvis oddzielną zmienną, nie tylko zmianą w v.W przypadku użycia rakiety do spowolnienia, tj. wyrzucenia masy reakcyjnej w kierunku prędkości, v powinno być ujemne.
Wzór jest dla idealnego przypadku, bez strat energii na ciepło, itp. To ostatnie powoduje zmniejszenie ciągu, więc jest wadą nawet wtedy, gdy celem jest utrata energii (opóźnienie).
Jeśli energia jest wytwarzana przez samą masę, jak w rakiecie chemicznej, wartość paliwa musi być 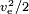 scriptstyle{v_text{e}^2/2}, gdzie dla wartości paliwa należy również uwzględnić masę utleniacza. Typową wartością jest ve= 4,5 km/s, co odpowiada wartości paliwa 10,1 MJ/kg. Rzeczywista wartość paliwa jest wyższa, ale duża część energii jest tracona jako ciepło odpadowe w spalinach, którego dysza nie była w stanie odebrać.
scriptstyle{v_text{e}^2/2}, gdzie dla wartości paliwa należy również uwzględnić masę utleniacza. Typową wartością jest ve= 4,5 km/s, co odpowiada wartości paliwa 10,1 MJ/kg. Rzeczywista wartość paliwa jest wyższa, ale duża część energii jest tracona jako ciepło odpadowe w spalinach, którego dysza nie była w stanie odebrać.
Wymagana energia E wynosi
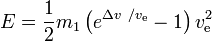
Wnioski:
- dla
 mamy
mamy 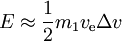
- dla danego Δv, minimalna energia jest potrzebna, jeśli ve =0.6275Δv, co wymaga energii równej
E = 0,772m1(Δv)2. Począwszy od prędkości zerowej jest to o 54,4 % więcej niż energia kinetyczna ładunku. W tym optymalnym przypadku masa początkowa jest 4,92 razy większa od masy końcowej.
Wyniki te dotyczą stałej prędkości wylotowej.
Ze względu na efekt Obertha i start z prędkości innej niż zerowa wymagana energia potencjalna potrzebna od materiału pędnego może być mniejsza niż przyrost energii w pojeździe i ładunku użytecznym. Tak może być w przypadku, gdy masa reakcyjna ma mniejszą prędkość po wyrzuceniu niż przed – rakiety są w stanie uwolnić część lub całość początkowej energii kinetycznej paliwa.
Ponadto, dla danego celu, takiego jak przejście z jednej orbity na drugą, wymagana Δv może w dużym stopniu zależeć od szybkości, z jaką silnik może wytworzyć Δv, a manewry mogą być nawet niemożliwe, jeśli szybkość ta jest zbyt mała. Na przykład, start na LEO normalnie wymaga Δv ok. 9,5 km/s (głównie w celu nabrania prędkości), ale jeśli silnik mógłby wytwarzać Δv z prędkością tylko nieco większą niż g, byłby to powolny start wymagający w sumie bardzo dużej Δv (pomyślmy o zawisaniu bez żadnego postępu w prędkości lub wysokości, kosztowałoby to Δv 9,8 m/s w każdej sekundzie). Jeśli możliwa prędkość wynosi tylko g lub mniej, manewr nie może być w ogóle wykonany przy pomocy tego silnika.
Moc jest dana przez
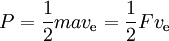
gdzie F jest siłą ciągu, a a przyspieszeniem spowodowanym przez nią. Teoretycznie możliwy ciąg na jednostkę mocy to 2 podzielone przez impuls jednostkowy w m/s. Sprawność ciągu to rzeczywisty ciąg jako procent tej wartości.
Jeśli np. energia słoneczna jest używana to ogranicza a; w przypadku dużego ve możliwe przyspieszenie jest odwrotnie proporcjonalne do niego, stąd czas osiągnięcia wymaganej delta-v jest proporcjonalny do ve; ze 100% wydajnością:
- dla
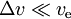 mamy
mamy 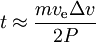 czas osiągnięcia wymaganejdelta-v}{2P}
czas osiągnięcia wymaganejdelta-v}{2P}
Przykłady:
- moc 1000 W, masa 100 kg, Δv=5 km/s, ve=16 km/s, trwa 1.5 months.
- power 1000 W, mass 100 kg, Δv=5 km/s, ve=50 km/s, takes 5 months.
Thus ve should notbe too large.
Derivation
Consider the following system:
In the following derivation, „the rocket” is taken to mean „therocket and all of its unburned propellant”. Newton’s second law ofmotion relates external forces (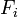 )to the change in linear momentum of the system as follows:
)to the change in linear momentum of the system as follows:
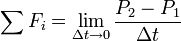
where 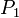 is the momentum of the rocket at time t=0:
is the momentum of the rocket at time t=0:
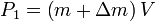
and 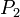 is the momentum of the rocket and exhausted mass at time
is the momentum of the rocket and exhausted mass at time  :
:
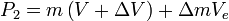
and where, with respect to the observer:
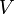 is thevelocity of the rocket at time t=0
is thevelocity of the rocket at time t=0
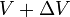 is thevelocity of the rocket at time
is thevelocity of the rocket at time 
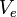 is thevelocity of the mass added to the exhaust (and lost by therocket) during time
is thevelocity of the mass added to the exhaust (and lost by therocket) during time 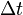
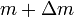 is the massof the rocket at time t=0
is the massof the rocket at time t=0
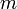 is the massof the rocket at time
is the massof the rocket at time 
The velocity of the exhaust Vein the observer frame is related to the velocity of the exhaust in therocket frame veby
Ve = V − ve
Solving yields:
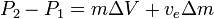
and
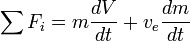
If there are no external forces then 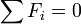 and
and
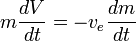
Zakładając, że 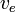 jest stała, to można ją zintegrować, aby otrzymać:
jest stała, to można ją zintegrować, aby otrzymać:
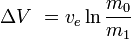
albo równoważnie
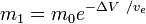 lub
lub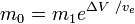
gdzie m0 jest początkową masą całkowitą zawierającą materiał pędny, a m1 – końcowa masa całkowita, a vet – prędkość wylotowa rakiety w stosunku do rakiety (impuls właściwy lub, jeżeli jest mierzony w czasie, pomnożony przez przyspieszenie ziemskie).
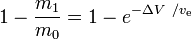 to ułamek masowy (część początkowej masy całkowitej, która jest wydatkowana jako masa reakcyjna).
to ułamek masowy (część początkowej masy całkowitej, która jest wydatkowana jako masa reakcyjna).
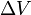 (delta v) to całkowanie w czasie wielkości przyspieszenia uzyskanego dzięki zastosowaniu silnika rakietowego (jakie byłoby rzeczywiste przyspieszenie, gdyby nie było sił zewnętrznych). W wolnej przestrzeni, dla przypadku przyspieszenia w kierunku prędkości, jest to wzrost prędkości. W przypadku przyspieszenia w przeciwnym kierunku (opóźnienia) jest to spadek prędkości.
(delta v) to całkowanie w czasie wielkości przyspieszenia uzyskanego dzięki zastosowaniu silnika rakietowego (jakie byłoby rzeczywiste przyspieszenie, gdyby nie było sił zewnętrznych). W wolnej przestrzeni, dla przypadku przyspieszenia w kierunku prędkości, jest to wzrost prędkości. W przypadku przyspieszenia w przeciwnym kierunku (opóźnienia) jest to spadek prędkości.
Oczywiście grawitacja i opór również przyspieszają pojazd i mogą dodawać lub odejmować do zmiany prędkości doświadczanej przez pojazd.Stąd delta-v nie jest zazwyczaj rzeczywistą zmianą prędkości lub prędkości pojazdu.
Pomimo, że jest to skrajne uproszczenie, równanie rakietowe ujmuje istotę fizyki lotu rakiety w jednym krótkim równaniu. Tak się składa, że delta-v jest jedną z najważniejszych wielkości w mechanice orbitalnej, która określa jak trudno jest wykonać dany manewr orbitalny.
Jasne jest, że aby osiągnąć dużą delta-v, albo m0musi być ogromne (rosnące wykładniczo wraz ze wzrostem delta-v), albo m1 musi być małe, albo ve musi być bardzo duże, albo jakaś kombinacja tych wszystkich.
W praktyce zostało to osiągnięte przez użycie bardzo dużych rakiet (zwiększających m0), wielostopniowych (zmniejszających m1) i rakiet o bardzo dużych prędkościach wylotowych. Rakiety Saturn V używane w programie kosmicznym Apollo i silniki jonowe używane w długodystansowych sondach bezzałogowych są tego dobrymi przykładami.
Rozwiązanie rakiety pokazuje rodzaj „wykładniczego spadku” masy m1, nie w funkcji czasu, ale w funkcji wytworzonej delta-v. Czas delta-v, który jest odpowiadającym „okresem połowicznego zaniku” wynosi 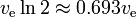
Przykłady
Załóżmy, że prędkość wylotowa wynosi 4.5 km/s, a Δv 9.7 km/s (Ziemia do LEO).
- Rakieta jednostopniowa na orbitę: 1 – e – 9.7 / 4.5= 0.884, zatem 88.4 % początkowej masy całkowitej musi stanowić materiał pędny. Pozostałe 11,6 % przypada na silniki, zbiornik i ładunek użyteczny. W przypadku promu kosmicznego, obejmuje to również orbiter.
- Dwa stopnie na orbitę:Załóżmy, że pierwszy stopień powinien zapewnić Δvof 5.0 km/s; 1 – e – 5.0 / 4.5= 0.671, zatem 67.1% początkowej masy całkowitej musi być materiałem pędnym do pierwszego stopnia. Pozostała masa wynosi 32,9%. Po wyrzuceniu pierwszego stopnia pozostaje masa równa owym 32.9 %, minus masa zbiornika i silników pierwszego stopnia. Zakładając, że jest to 8 % początkowej masy całkowitej, pozostaje 24,9 %. Drugi stopień powinien zapewnić Δv równą 4,7 km/s; 1 – e – 4,7 / 4,5= 0,648, zatem 64,8 % pozostałej masy musi stanowić materiał pędny, czyli 16,2 %, a 8,7 % pozostaje na zbiornik i silniki drugiego stopnia, ładunek użyteczny, a w przypadku promu kosmicznego także na orbitera. Tak więc razem 16,7 % jest dostępne dla wszystkich silników, zbiorników, ładunku użytecznego i ewentualnego orbitera.
Zastosowanie
Równanie rakietowe jest prawdziwe dla rakietopodobnych pojazdów reakcyjnych, gdy efektywna prędkość wylotowa jest stała; i może być sumowane lub całkowane, gdy efektywna prędkość wylotowa się zmienia.
Nie ma jednak zastosowania do innych technologii, takich jak wyrzutnie, windy kosmiczne, pętle startowe, napęd na uwięzi i silniki oddychające powietrzem.
Zobacz także
- Delta-v
- Budżet delta-v
- Efekt Obertha zastosowanie delta-v in a gravitywell increases the final velocity
- Specific impulse
- Spacecraft propulsion
- Mass ratio
- Working mass
- Relativistic rocket
- Reversibility oforbits
|
|
This article includes a list of references, but itssources remain unclear because it has insufficient inline citations. Please help to improvethis article by introducing more precise citations where appropriate. (February2009) |
- ^К. Э. Циолковский, Исследование мировых пространств реактивнымиприборами, 1903. It is available online here in a RARed PDF
- ^ Moore, William; ofthe MilitaryAcademy at Woolwich (1813). A Treatise on the Motion ofRockets. To which is added, An Essay on Naval Gunnery. London: G.and S. Robinson.
- ^ Johnson, W. (1995). „Contents and commentary onWilliam Moore’s a treatise on the motion of rockets and an essay onnaval gunnery”. International Journal of Impact Engineering 16 (3): 499–521. doi:10.1016/0734-743X(94)00052-X. ISSN 0734-743X. http://www.sciencedirect.com/science/article/B6V3K-3Y5FP5P-11/2/c3e98a6cec8f083c93dc4e4e157282bb.
- How to derive the rocket equation
- Relativity Calculator – LearnTsiolkovsky’s rocket equations