| Astrodynamics | ||
| Orbital mechanics | Equations | Efficiencymeasures |
|---|---|---|
| v · d · e |
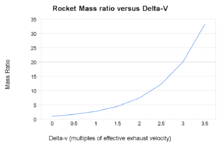
Raportul masei rachetei în funcție de viteza finală calculată din ecuația rachetei
Ecuația rachetei Tsiolkovsky, sau ecuația rachetei ideale,este o ecuație matematică care relaționează delta-v (modificarea maximă a vitezei rachetei dacă nu acționează alte forțe externe) cu viteza efectivă de evacuare și cu masa inițială și finală a unei rachete sau a unui alt motor de reacție.
Ecuația poartă numele lui KonstantinTsiolkovsky, care a derivat-o independent și a publicat-o în lucrarea sa din 1903.Ea are în vedere principiul unei rachete:un dispozitiv care își poate aplica o accelerație (o împingere)prin expulzarea unei părți din masa sa cu viteză mare în direcția opusă datorită conservării impulsului.
Pentru orice astfel de manevră (sau călătorie care implică un număr de astfel de manevre):
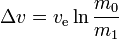
where:
m0 is the initialtotal mass, including propellant. m1 is the finaltotal mass. ve is the effectiveexhaust velocity. (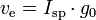 where Isp is the specific impulse expressed as a timeperiod)
where Isp is the specific impulse expressed as a timeperiod) 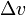 is delta-v-the maximum change of speed of the vehicle (with noexternal forces acting)
is delta-v-the maximum change of speed of the vehicle (with noexternal forces acting)
Units used for mass or velocity do not matter as long as they areconsistent.
- 1 History
- 2 Stages
- 3 Energy
- 4 Derivation
- 5 Examples
- 6 Applicability
- 7 See also
- 8 References
- 9 External links
History
This equation was independently derived by Konstantin Tsiolkovsky towards theend of the 19th century and is widely known under this name and idealrocket equation. Cu toate acestea, o broșură recent descoperită „A Treatiseon the Motion of Rockets” de William Moorespune că cea mai veche derivare cunoscută a acestui tip de ecuație a fost de fapt la Academia Militară Regală dinWoolwichîn Anglia în 1813 și a fost folosită pentru cercetarea în domeniul armelor.
Etaje
În cazul etajelor de rachetă cu propulsie secvențială, ecuația se aplică pentru fiecare etaj, unde, pentru fiecare etaj, masa inițială din ecuație este masa totală a rachetei după eliminarea etajului anterior, iar masa finală din ecuație este masa totală a rachetei chiar înainte de eliminarea etajului respectiv. Pentru fiecare etapă, impulsul specific poate fi diferit.
De exemplu, dacă 80% din masa unei rachete reprezintă combustibilul primei trepte, 10% reprezintă masa uscată a primei trepte și 10% reprezintă racheta rămasă, atunci
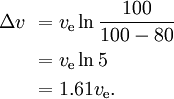
Cu trei etape similare, ulterior mai mici, cu același ve pentru fiecare etapă, avem
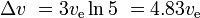
și sarcina utilă este de 10%*10%*10%*10% = 0,1% din masa inițială.
O rachetă SSTO comparabilă, tot cu o sarcină utilă de 0,1%, ar putea avea o masă de 11% pentru rezervoare și motoare și 88,9%pentru combustibil. Acest lucru ar da
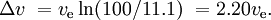
Dacă motorul unei noi etape este aprins înainte ca etapa precedentă să fi fost eliminată și dacă motoarele care funcționează simultan au un impuls specific diferit (așa cum se întâmplă adesea în cazul rachetelor de propulsie cu combustibil solid și al etajelor cu combustibil lichid), situația este mai complicată.
Energie
În cazul ideal m1este sarcina utilă și m0 – m1este masa de reacție (aceasta corespunde rezervoarelor goale care nu au masă,etc.). Energia necesară poate fi calculată simplu ca
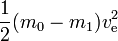
Aceasta corespunde energiei cinetice pe care masa de reacție expulzată ar avea-o la o viteză egală cu viteza de evacuare. Dacă masa de reacție ar trebui să fie accelerată de la viteza zero la viteza de evacuare, toată energia produsă ar intra în masa de reacție și nu ar mai rămâne nimic pentru obținerea energiei cinetice de către rachetă și încărcătura utilă. Cu toate acestea, dacă racheta se deplasează deja și accelerează (masa de reacție este expulzată în direcția opusă celei în care se deplasează racheta), se adaugă mai puțină energie cinetică la masa de reacție. Pentru a vedea acest lucru, dacă, de exemplu, ve=10 km/s și viteza rachetei este de 3 km/s, atunci viteza unei cantități mici de masă de reacție expulzată se schimbă de la 3 spre înainte la 7 km/s spre înapoi. Astfel, în timp ce energia necesară este de 50 MJ pe kg de masă de reacție, doar 20 MJ sunt utilizați pentru creșterea vitezei masei de reacție. Restul de 30 MJ reprezintă creșterea energiei cinetice a rachetei și a încărcăturii utile.
În general:
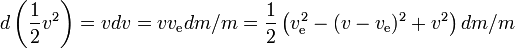
Astfel, câștigul specific de energie al rachetei în orice interval de timp mic este câștigul de energie al rachetei, inclusiv combustibilul rămas,împărțit la masa sa, unde câștigul de energie este egal cu energia produsă de combustibil minus câștigul de energie al masei de reacție. Cu cât viteza rachetei este mai mare, cu atât câștigul de energie al masei de reacție este mai mic; dacă viteza rachetei este mai mare de jumătate din viteza de evacuare, masa de reacție pierde chiar energie la expulzare, în beneficiul câștigului de energie al rachetei; cu cât viteza rachetei este mai mare, cu atât pierderea de energie a masei de reacție este mai mare.
Avem
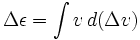
unde ε este energia specifică a rachetei (energia potențială plus energia cinetică) și Δvis o variabilă separată, nu doar variația lui v.În cazul folosirii rachetei pentru decelerare, adică pentru a expulza masa de reacție în direcția vitezei, vtrebuie luată negativă.
Formula este din nou pentru cazul ideal, fără pierderi de energie din cauza încălzirii etc. Aceasta din urmă determină o reducere a împingerii, deci este un dezavantaj chiar și atunci când obiectivul este de a pierde energie (decelerare).
Dacă energia este produsă de masa însăși, ca într-o rachetă chimică, valoarea combustibilului trebuie să fie 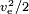 ,unde pentru valoarea combustibilului trebuie luată în considerare și masa oxidantului. O valoare tipică este ve= 4,5 km/s, ceea ce corespunde unei valori a combustibilului de 10,1 MJ/kg. Valoarea reală a combustibilului este mai mare, dar o mare parte din energie este pierdută sub formă de căldură reziduală în gazele de eșapament pe care duza nu a reușit să o extragă.
,unde pentru valoarea combustibilului trebuie luată în considerare și masa oxidantului. O valoare tipică este ve= 4,5 km/s, ceea ce corespunde unei valori a combustibilului de 10,1 MJ/kg. Valoarea reală a combustibilului este mai mare, dar o mare parte din energie este pierdută sub formă de căldură reziduală în gazele de eșapament pe care duza nu a reușit să o extragă.
Energia necesară E este
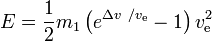
Concluzii:
- pentru
 avem
avem 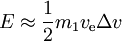
- pentru un Δv dat, energia minimă este necesară dacă ve =0.6275Δv, fiind necesară o energie de
E = 0,772m1(Δv)2. Pornind de la viteza zero, aceasta este cu 54,4 % mai mult decât doar energia cinetică a încărcăturii utile. În acest caz optim, masa inițială este de 4,92 ori mai mare decât masa finală.
Aceste rezultate se aplică pentru o viteză de evacuare fixă.
Datorită efectului Oberth și pornind de la o viteză diferită de zero, energia potențială necesară necesară din propulsor poate fi mai mică decât creșterea energiei din vehicul și din sarcina utilă. Acesta poate fi cazul atunci când masa de reacție are o viteză mai mică după ce este expulzată decât înainte- rachetele sunt capabile să elibereze o parte sau toată energia cinetică inițială a propulsorului.
De asemenea, pentru un obiectiv dat, cum ar fi deplasarea de pe o orbită pe alta, Δv-ul necesar poate depinde foarte mult de viteza cu care motorul poate produce Δv, iar manevrele pot fi chiar imposibile dacă această viteză este prea mică. De exemplu, o lansare către LEO necesită în mod normal un Δv de aproximativ 9,5 km/s (mai ales pentru ca viteza să fie dobândită), dar dacă motorul ar putea produce Δv la o rată de numai puțin mai mare decât g, ar fi o lansare lentă care ar necesita în total un Δv foarte mare (gândiți-vă că ar trebui să staționați fără să faceți nici un progres în viteză sau altitudine, ar costa un Δv de 9,8 m/s în fiecare secundă). Dacă rata posibilă este doar g sau mai mică, manevra nu se poate realiza deloc cu acest motor.
Puterea este dată de
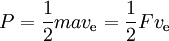
unde F este împingerea și a accelerația datorată acesteia. Astfel, împingerea teoretic posibilă pe unitatea de putere este 2 împărțit la impulsul specific în m/s. Eficiența împingerii este împingerea reală ca procent din aceasta.
Dacă de ex. energie solară, acest lucru limitează a; în cazul unei ve mari, accelerația posibilă este invers proporțională cu aceasta, prin urmare, timpul necesar pentru a atinge delta-v este proporțional cu ve; cu o eficiență de 100%:
- pentru
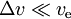 avem
avem 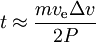
Exemple:
- putere 1000 W, masă 100 kg, Δv=5 km/s, ve=16 km/s, durează 1.5 months.
- power 1000 W, mass 100 kg, Δv=5 km/s, ve=50 km/s, takes 5 months.
Thus ve should notbe too large.
Derivation
Consider the following system:
In the following derivation, „the rocket” is taken to mean „therocket and all of its unburned propellant”. Newton’s second law ofmotion relates external forces (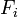 )to the change in linear momentum of the system as follows:
)to the change in linear momentum of the system as follows:
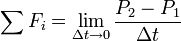
where 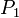 is the momentum of the rocket at time t=0:
is the momentum of the rocket at time t=0:
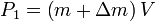
and 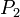 is the momentum of the rocket and exhausted mass at time
is the momentum of the rocket and exhausted mass at time  :
:
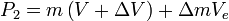
and where, with respect to the observer:
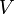 is thevelocity of the rocket at time t=0
is thevelocity of the rocket at time t=0
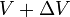 is thevelocity of the rocket at time
is thevelocity of the rocket at time 
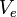 is thevelocity of the mass added to the exhaust (and lost by therocket) during time
is thevelocity of the mass added to the exhaust (and lost by therocket) during time 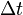
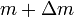 is the massof the rocket at time t=0
is the massof the rocket at time t=0
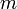 is the massof the rocket at time
is the massof the rocket at time 
The velocity of the exhaust Vein the observer frame is related to the velocity of the exhaust in therocket frame veby
Ve = V − ve
Solving yields:
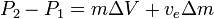
and
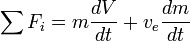
If there are no external forces then 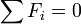 and
and
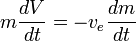
Să presupunem că 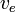 este constantă, aceasta poate fi integrată pentru a obține:
este constantă, aceasta poate fi integrată pentru a obține:
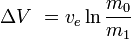
sau, în mod echivalent
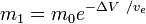 sau
sau 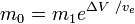
unde m0 este masa totală inițială, inclusiv propulsoarele, iar m1masa totală finală și vetviteza de evacuare a rachetei în raport cu racheta (impulsul specific sau, dacă este măsurat în timp, acesta înmulțit cu accelerația gravitațională pe Pământ).
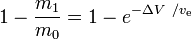 este fracția de masă (partea din masa totală inițială care este cheltuită ca masă de reacție).
este fracția de masă (partea din masa totală inițială care este cheltuită ca masă de reacție).
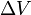 (delta v) este integrarea în timp a mărimii accelerației produse de utilizarea motorului-rachetă (care ar fi accelerația reală dacă forțele externe ar fi absente). În spațiul liber, în cazul unei accelerații în direcția vitezei, aceasta reprezintă creșterea vitezei. În cazul unei accelerații în direcția opusă (decelerare), aceasta reprezintă scăderea vitezei.
(delta v) este integrarea în timp a mărimii accelerației produse de utilizarea motorului-rachetă (care ar fi accelerația reală dacă forțele externe ar fi absente). În spațiul liber, în cazul unei accelerații în direcția vitezei, aceasta reprezintă creșterea vitezei. În cazul unei accelerații în direcția opusă (decelerare), aceasta reprezintă scăderea vitezei.
Desigur, gravitația și rezistența la înaintare accelerează, de asemenea, vehiculul și pot adăuga sau scădea modificarea vitezei experimentate de vehicul.Prin urmare, delta-v nu reprezintă, de obicei, modificarea reală a vitezei sau a vitezei vehiculului.
Deși reprezintă o simplificare extremă, ecuația rachetei surprinde elementele esențiale ale fizicii zborului cu rachetă într-o singură ecuație scurtă. De asemenea, se întâmplă că delta-v este una dintre cele mai importante mărimi din mecanica orbitală, care cuantifică cât de dificilă este efectuarea unei anumite manevre orbitale.
Evident, pentru a obține o delta-v mare, fie m0trebuie să fie imensă (crescând exponențial pe măsură ce delta-v crește), fie m1trebuie să fie mică, fie ve trebuie să fie foarte mare, fie o combinație a tuturor acestora.
În practică, acest lucru a fost realizat prin utilizarea unor rachete foarte mari (crescând m0), cu mai multe etaje (scăzând m1), și a unor rachete cu viteze de evacuare foarte mari. Rachetele Saturn V folosite în programul spațial Apolloși propulsoarele ionice folosite în sondele fără pilot la distanțe lungi sunt exemple bune în acest sens.
Ecuația rachetei arată un fel de „descreștere exponențială” a masei m1, nu în funcție de timp, ci în funcție de delta-v produsă. Delta-v care este „timpul de înjumătățire” corespunzător este 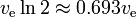
Exemple
Să presupunem o viteză de evacuare de 4,5 km/s și un Δv de 9,7 km/s (de la Pământ la LEO).
- Rachetă cu un singur etaj până la orbită: 1 – e – 9,7 / 4,5 = 0,884, prin urmare 88,4 % din masa totală inițială trebuie să fie combustibil. Restul de 11,6 % este pentru motoare, rezervor și sarcina utilă. În cazul unei navete spațiale, aceasta ar include, de asemenea, și absorbantul.
- Două etape până la orbită: să presupunem că prima etapă ar trebui să asigure un Δvo de 5,0 km/s; 1 – e – 5,0 / 4,5= 0,671, prin urmare 67,1 % din masa totală inițială trebuie să fie propulsorpentru prima etapă. Masa rămasă este de 32,9 %. După eliminarea primei etape, rămâne o masă egală cu aceste 32.9 %, minus masa rezervorului și a motoarelor din prima etapă. Presupunând că aceasta reprezintă 8 % din masa totală inițială, rămân 24,9 %. Această a doua treaptă ar trebui să asigure un Δvo de 4,7 km/s; 1 – e – 4,7 / 4,5 = 0,648, prin urmare 64,8 % din masa rămasă trebuie să fie propulsor, ceea ce înseamnă 16,2 %, iar 8,7 % rămân pentru rezervorul și motoarele celei de-a doua trepte, pentru sarcina utilă și, în cazul unei navete spațiale, și pentru orbitor. Astfel, împreună, 16,7 % sunt disponibile pentru toate motoarele, rezervoarele, încărcătura utilă și eventualul orbitator.
Aplicabilitate
Ecuația rachetei este valabilă pentru vehiculele de reacție de tip rachetă ori de câte ori viteza efectivă de evacuare este constantă; și poate fi însumată sau integrată atunci când viteza efectivă de evacuare variază.
Cu toate acestea, nu se aplică altor tehnologii, cum ar fi lansările cu tunuri, ascensoarele spațiale, buclele de lansare, propulsia cu cabluri și motoarele cu respirație pneumatică.
Vezi și
- Delta-v
- Bilanț delta-v
- Efectul Oberth care aplică delta-v in a gravitywell increases the final velocity
- Specific impulse
- Spacecraft propulsion
- Mass ratio
- Working mass
- Relativistic rocket
- Reversibility oforbits
|
|
This article includes a list of references, but itssources remain unclear because it has insufficient inline citations. Please help to improvethis article by introducing more precise citations where appropriate. (February2009) |
- ^К. Э. Циолковский, Исследование мировых пространств реактивнымиприборами, 1903. It is available online here in a RARed PDF
- ^ Moore, William; ofthe MilitaryAcademy at Woolwich (1813). A Treatise on the Motion ofRockets. To which is added, An Essay on Naval Gunnery. London: G.and S. Robinson.
- ^ Johnson, W. (1995). „Contents and commentary onWilliam Moore’s a treatise on the motion of rockets and an essay onnaval gunnery”. International Journal of Impact Engineering 16 (3): 499–521. doi:10.1016/0734-743X(94)00052-X. ISSN 0734-743X. http://www.sciencedirect.com/science/article/B6V3K-3Y5FP5P-11/2/c3e98a6cec8f083c93dc4e4e157282bb.
- How to derive the rocket equation
- Relativity Calculator – LearnTsiolkovsky’s rocket equations