| Astrodynamics | ||
| Orbital mechanics | Equations | Efficiencymeasures |
|---|---|---|
| v · d · e |
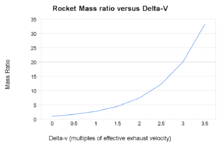
Raketové hmotnostní poměry v závislosti na konečné rychlosti vypočtenéz raketové rovnice
Ciolkovského raketová rovnice, neboli rovnice ideální rakety, je matematická rovnice, která spojuje delta-v (maximální změnu rychlosti rakety, pokud nepůsobí žádné jiné vnější síly) s efektivní výfukovou rychlostí a počáteční a konečnou hmotností rakety nebo jiného reakčního motoru.
Rovnice je pojmenována po KonstantinuCjolkovském, který ji nezávisle odvodil a publikoval ve své práci z roku 1903.
Zohledňuje princip rakety:zařízení, které na sebe může působit zrychlením (tahem)tím, že vypudí část své hmoty velkou rychlostí opačným směremv důsledku zachování hybnosti.
Pro každý takový manévr (nebo cestu zahrnující několik takových manévrů):
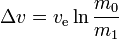
where:
m0 is the initialtotal mass, including propellant. m1 is the finaltotal mass. ve is the effectiveexhaust velocity. (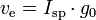 where Isp is the specific impulse expressed as a timeperiod)
where Isp is the specific impulse expressed as a timeperiod)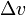 is delta-v-the maximum change of speed of the vehicle (with noexternal forces acting)
is delta-v-the maximum change of speed of the vehicle (with noexternal forces acting)
Units used for mass or velocity do not matter as long as they areconsistent.
- 1 History
- 2 Stages
- 3 Energy
- 4 Derivation
- 5 Examples
- 6 Applicability
- 7 See also
- 8 References
- 9 External links
History
This equation was independently derived by Konstantin Tsiolkovsky towards theend of the 19th century and is widely known under this name and idealrocket equation. Nedávno objevená brožura „A Treatiseon the Motion of Rockets“ od Williama Mooreše však ukazuje, že nejstarší známé odvození tohoto druhu rovnice bylove skutečnosti na Královské vojenské akademii veWoolwichi v Anglii v roce 1813 a bylo použito pro výzkum zbraní.
Stupně
V případě postupně táhnoucích raketových stupňů platí tato rovnice pro každý stupeň, přičemž pro každý stupeň je počáteční hmotnost v rovnici celková hmotnost rakety po vyřazení předchozího stupně a konečná hmotnost v rovnici je celková hmotnost rakety těsně před vyřazením příslušného stupně. Pro každou etapu může být specifický impuls jiný.
Příklad pokud 80 % hmotnosti rakety tvoří palivo prvního stupně, 10 % suchá hmotnost prvního stupně a 10 % zbývající část rakety, pak
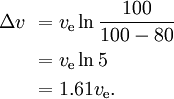
Při třech podobných, následně menších stupních se stejným ve pro každý stupeň máme
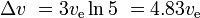
a užitečné zatížení je 10 %*10 %*10 % = 0,1 % počáteční hmotnosti.
Srovnatelná raketa SSTO, rovněž s užitečným zatížením 0,1 %, by mohla mít hmotnost 11 % pro palivové nádrže a motory a 88,9 % pro palivo. To by dávalo
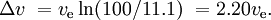
Jestliže je motor nového stupně zapálen před vyřazením předchozího stupně a současně pracující motory mají rozdílný specifický impuls (jak je tomu často u raketových nosičů na tuhé a kapalné palivo), je situace složitější.
Energie
V ideálním případě je m1užitečné zatížení a m0 – m1 reakční hmotnost (to odpovídá prázdným nádržím, které nemají žádnou hmotnost atd.). Potřebnou energii lze jednoduše vypočítat jako
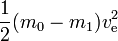
To odpovídá kinetické energii, kterou by měla vypuzená reakční hmota při rychlosti rovné rychlosti výfuku. Pokud by reakční hmota musela být urychlena z nulové rychlosti na rychlost výfuku, veškerá vyrobená energie by přešla do reakční hmoty a raketě a užitečnému zatížení by nezbylo nic na získání kinetické energie. Pokud se však raketa již pohybuje a zrychluje (reakční hmota je vypuzena ve směru opačném ke směru pohybu rakety), je reakční hmotě přidáno méně kinetické energie. Abychom to viděli, pokud je například ve=10 km/s a rychlost rakety je 3 km/s, pak se rychlost malého množství vypuštěné reakční hmoty změní z 3 dopředu na 7 km/s dozadu. Ačkoli je tedy potřeba energie 50 MJ na 1 kg reakční hmoty, na zvýšení rychlosti reakční hmoty se spotřebuje pouze 20 MJ. Zbývajících 30 MJ představuje zvýšení kinetické energie rakety a užitečného zatížení.
Všeobecně:
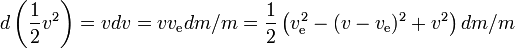
Takto je měrný zisk energie rakety v jakémkoli malém časovém intervalu ziskem energie rakety včetně zbývajícího paliva,dělený její hmotností, přičemž energetický zisk se rovná energii vyprodukované palivem minus energetický zisk reakční hmoty. Čím větší je rychlost rakety, tím menší je energetický zisk reakční hmoty; je-li rychlost rakety větší než polovina rychlosti výfuku, reakční hmota při vypuzení dokonce ztrácí energii ve prospěch energetického zisku rakety; čím větší je rychlost rakety, tím větší je energetická ztráta reakční hmoty.
Máme
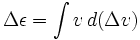
kde ε je specifická energie rakety (potenciální plus kinetická energie) a Δje samostatná veličina, nikoliv pouze změna v.V případě použití rakety ke zpomalení, tj. vypuzeníreakční hmoty ve směru rychlosti, by vs mělo být záporné.
Vzorec je opět pro ideální případ, bez ztrát energie na teplo atd. Ta způsobuje snížení tahu, takže je nevýhodná i v případě, kdy je cílem ztráta energie (zpomalení).
Pokud je energie produkována samotnou hmotou, jako v chemické raketě, musí být hodnota paliva 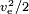 ,kde pro hodnotu paliva musí být zohledněna i hmotnost okysličovadla. Typická hodnota je ve= 4,5 km/s, což odpovídá hodnotě paliva 10,1 MJ/kg. Skutečná hodnota paliva je vyšší, ale velká část energie se ztrácí jako odpadní teplo ve výfukových plynech, které tryska nedokázala odebrat.
,kde pro hodnotu paliva musí být zohledněna i hmotnost okysličovadla. Typická hodnota je ve= 4,5 km/s, což odpovídá hodnotě paliva 10,1 MJ/kg. Skutečná hodnota paliva je vyšší, ale velká část energie se ztrácí jako odpadní teplo ve výfukových plynech, které tryska nedokázala odebrat.
Potřebná energie E je
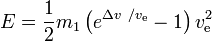
Závěry:
- pro
 máme
máme 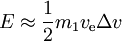
- pro dané Δv je potřeba minimální energie, pokud ve =0.6275Δv, což vyžaduje energii
E = 0,772m1(Δv)2. Počínaje nulovou rychlostí je to o 54,4 % více než pouhá kinetická energie užitečného zatížení. V tomto optimálním případě je počáteční hmotnost4,92násobkem konečné hmotnosti.
Tyto výsledky platí pro pevnou rychlost výfuku.
V důsledku Oberthova jevu a při startu z jiné než nulové rychlosti může být požadovaná potenciální energie potřebná z pohonné hmoty menší než nárůst energie ve vozidle a užitečném zatížení. To může nastat v případě, že reakční hmota má po vypuzení nižší rychlost než předtím – rakety jsou schopny uvolnit část nebo celou počáteční kinetickou energii pohonné hmoty.
Pro daný cíl, jako je přesun z jedné oběžné dráhy na druhou, může také požadovaná Δv značně záviset na rychlosti, kterou může motor vytvářet Δv, a manévry mohou být dokonce nemožné, pokud je tato rychlost příliš nízká. Například start na LEO obvykle vyžaduje Δv přibližně 9,5 km/s (hlavně pro získání rychlosti), ale pokud by motor mohl produkovat Δv rychlostí jen o málo větší než g, jednalo by se o pomalý start vyžadující celkem velmi velké Δv (představte si visení bez jakéhokoli pokroku v rychlosti nebo výšce, stálo by to Δv 9,8 m/s každou sekundu). Pokud je možná rychlost pouze g nebo menší, nelze s tímto motorem manévr vůbec provést.
Výkon je dán vztahem
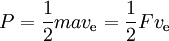
kde F je tah a a zrychlení z něj plynoucí. Teoreticky možný tah na jednotku výkonu je tedy 2 děleno specifickým impulsem v m/s. Účinnost tahu je skutečný tah vyjádřený v procentech.
Pokud je např. se používá solární energie, omezuje to a; v případě velkého ve je možné zrychlení nepřímo úměrné, tudíž čas k dosažení požadovanéhodelta-v je úměrný ve;se100% účinností:
- pro
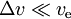 máme
máme 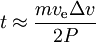
Příklad:
- výkon 1000 W, hmotnost 100 kg, Δv=5 km/s, ve=16 km/s, trvá 1.5 months.
- power 1000 W, mass 100 kg, Δv=5 km/s, ve=50 km/s, takes 5 months.
Thus ve should notbe too large.
Derivation
Consider the following system:
In the following derivation, „the rocket“ is taken to mean „therocket and all of its unburned propellant“. Newton’s second law ofmotion relates external forces (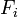 )to the change in linear momentum of the system as follows:
)to the change in linear momentum of the system as follows:
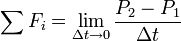
where 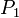 is the momentum of the rocket at time t=0:
is the momentum of the rocket at time t=0:
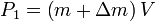
and 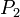 is the momentum of the rocket and exhausted mass at time
is the momentum of the rocket and exhausted mass at time  :
:
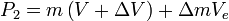
and where, with respect to the observer:
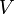 is thevelocity of the rocket at time t=0
is thevelocity of the rocket at time t=0
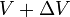 is thevelocity of the rocket at time
is thevelocity of the rocket at time 
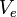 is thevelocity of the mass added to the exhaust (and lost by therocket) during time
is thevelocity of the mass added to the exhaust (and lost by therocket) during time 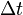
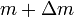 is the massof the rocket at time t=0
is the massof the rocket at time t=0
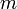 is the massof the rocket at time
is the massof the rocket at time 
The velocity of the exhaust Vein the observer frame is related to the velocity of the exhaust in therocket frame veby
Ve = V − ve
Solving yields:
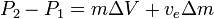
and
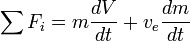
If there are no external forces then 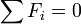 and
and
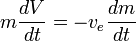
Podle 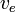 je konstantní, lze tuto hodnotu integrovat a získat následující výsledek:
je konstantní, lze tuto hodnotu integrovat a získat následující výsledek:
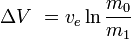
nebo ekvivalentně
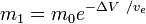 nebo
nebo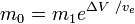
kde m0 je počáteční celková hmotnost včetně pohonné látky, a m1konečná celková hmotnost a vetrychlost výfukových plynů rakety vzhledem k raketě (specifický impuls, nebo, pokud se měří v čase, vynásobený tíhovým zrychlením na Zemi).
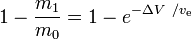 je hmotnostní podíl (část počáteční celkové hmotnosti, která se spotřebuje jako reakční hmotnost).
je hmotnostní podíl (část počáteční celkové hmotnosti, která se spotřebuje jako reakční hmotnost).
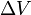 (delta v) je integrace v čase velikosti zrychlení vzniklého použitím raketového motoru (jaké by bylo skutečné zrychlení, kdyby neexistovaly vnější síly). Ve volném prostoru se v případě zrychlení ve směru rychlosti jedná o nárůst rychlosti. V případě zrychlení v opačném směru (zpomalení) se jedná o snížení rychlosti.
(delta v) je integrace v čase velikosti zrychlení vzniklého použitím raketového motoru (jaké by bylo skutečné zrychlení, kdyby neexistovaly vnější síly). Ve volném prostoru se v případě zrychlení ve směru rychlosti jedná o nárůst rychlosti. V případě zrychlení v opačném směru (zpomalení) se jedná o snížení rychlosti.
Gravitace a odpor vzduchu samozřejmě také zrychlují vozidlo a mohou přidávat nebo ubírat na změně rychlosti, kterou vozidlo zažívá.Proto delta-v obvykle není skutečnou změnou rychlosti nebo rychlosti vozidla.
Ačkoli se jedná o extrémní zjednodušení, raketová rovnice zachycuje podstatu fyziky raketového letu v jediné krátké rovnici. Také se stává, že delta-v je jednou z nejdůležitějších veličin v orbitálnímechanice, která kvantifikuje, jak obtížné je provést daný orbitální manévr.
Je zřejmé, že k dosažení velkého delta-v musí být buď m0 obrovské (roste exponenciálně s nárůstem delta-v), nebo m1 musí být malé, nebo ve musí být velmi vysoké, nebo nějaká kombinace všech těchto možností.
V praxi se toho dosahuje použitím velmi velkých raket (zvyšujících m0), s více stupni (snižujících m1) a raket s velmi vysokými výfukovými rychlostmi. Dobrým příkladem jsou rakety Saturn V používané v kosmickém programu Apollo a iontové trysky používané v bezpilotních sondách na dlouhé vzdálenosti.
Raketová rovnice ukazuje jakýsi „exponenciální rozpad“ hmotnosti m1, nikoliv však jako funkci času, ale jako funkci vyprodukovaného delta-v. Delta-v, která odpovídá „poločasu rozpadu“, je 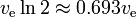
Příklady
Předpokládejme rychlost výfuku 4,5 km/s a Δv 9,7 km/s (ze Země na LEO).
- Jednostupňová raketa na oběžnou dráhu: 1 – e – 9,7 / 4,5= 0,884, proto 88,4 % počáteční celkové hmotnosti musí tvořit pohonná hmota. Zbývajících 11,6 % připadá na motory, nádrž a užitečné zatížení. V případě raketoplánu by zahrnovala také orbitální modul.
- Dva stupně na oběžnou dráhu:předpokládejme, že první stupeň by měl zajistit rychlost Δvo5,0 km/s; 1 – e – 5,0 / 4,5= 0,671, proto 67,1 % počáteční celkové hmotnosti musí tvořit pohonná hmota prvního stupně. Zbývající hmotnost činí 32,9 %. Po vyřazení prvního stupně zbývá hmotnost rovnající se těmto 32.9 %, po odečtení hmotnosti nádrže a motorů prvního stupně. Předpokládejme, že to je 8 % počáteční celkové hmotnosti, pak zbývá 24,9 %. Druhý stupeň by měl zajistit rychlost Δvo 4,7 km/s; 1 – e – 4,7 / 4,5 = 0,648, proto 64,8 % zbývající hmotnosti musí tvořit pohonná hmota, což je 16,2 %, a 8,7 % zbývá na nádrž a motory druhého stupně, užitečné zatížení a v případě raketoplánu také na oběžnou dráhu. Dohromady je tedy k dispozici 16,7 % pro všechny motory, nádrže, užitečné zatížení a případný orbiter.
Použitelnost
Raketová rovnice platí pro reaktivní vozidla typu rakety, kdykoli je efektivní rychlost výfuku konstantní; a může být sečtena nebo integrována, když se efektivní rychlost výfuku mění.
Neplatí však pro jiné technologie, jako jsou dělové motory, kosmické výtahy, startovací smyčky, upoutané motory a motory dýchající vzduch.
Viz také
- Delta-v
- Delta-v rozpočet
- Oberthův efekt uplatňující delta-v in a gravitywell increases the final velocity
- Specific impulse
- Spacecraft propulsion
- Mass ratio
- Working mass
- Relativistic rocket
- Reversibility oforbits
|
|
This article includes a list of references, but itssources remain unclear because it has insufficient inline citations. Please help to improvethis article by introducing more precise citations where appropriate. (February2009) |
- ^К. Э. Циолковский, Исследование мировых пространств реактивнымиприборами, 1903. It is available online here in a RARed PDF
- ^ Moore, William; ofthe MilitaryAcademy at Woolwich (1813). A Treatise on the Motion ofRockets. To which is added, An Essay on Naval Gunnery. London: G.and S. Robinson.
- ^ Johnson, W. (1995). „Contents and commentary onWilliam Moore’s a treatise on the motion of rockets and an essay onnaval gunnery“. International Journal of Impact Engineering 16 (3): 499–521. doi:10.1016/0734-743X(94)00052-X. ISSN 0734-743X. http://www.sciencedirect.com/science/article/B6V3K-3Y5FP5P-11/2/c3e98a6cec8f083c93dc4e4e157282bb.
- How to derive the rocket equation
- Relativity Calculator – LearnTsiolkovsky’s rocket equations