| Astrodynamics | ||
| Orbital mechanics | Equations | Efficiencymeasures |
|---|---|---|
| v · d · e |
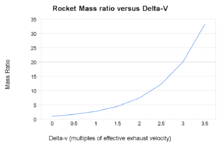
Rakéta tömegarányok a rakétaegyenletből számított végsebességhez képest
A Csiolkovszkij rakétaegyenlet, vagy ideális rakétaegyenlet,egy matematikai egyenlet, amely a delta-v-t (a rakéta maximális sebességváltozását, ha nem hatnak más külső erők) a tényleges kipufogógázsebességgel és a rakéta vagy más reakcióhajtómű kezdeti és végső tömegével hozza összefüggésbe.
Az egyenlet Konsztantyin Csiolkovszkijról kapta a nevét, aki önállóan vezette le és publikálta1903-ban megjelent munkájában.A rakéta alapelve:egy olyan eszköz, amely úgy képes gyorsulást (tolóerőt)kifejteni önmagára, hogy tömegének egy részét nagy sebességgel az ellenkező irányba löki ki a lendületmegmaradás miatt.
Minden ilyen manőverre (vagy több ilyen manőverből álló útra):
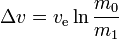
where:
m0 is the initialtotal mass, including propellant. m1 is the finaltotal mass. ve is the effectiveexhaust velocity. (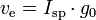 where Isp is the specific impulse expressed as a timeperiod)
where Isp is the specific impulse expressed as a timeperiod)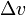 is delta-v-the maximum change of speed of the vehicle (with noexternal forces acting)
is delta-v-the maximum change of speed of the vehicle (with noexternal forces acting)
Units used for mass or velocity do not matter as long as they areconsistent.
- 1 History
- 2 Stages
- 3 Energy
- 4 Derivation
- 5 Examples
- 6 Applicability
- 7 See also
- 8 References
- 9 External links
History
This equation was independently derived by Konstantin Tsiolkovsky towards theend of the 19th century and is widely known under this name and idealrocket equation. Azonban egy nemrég felfedezett William Mooresh “A Treatiseon the Motion of Rockets” című röpiratából kiderül, hogy az ilyen típusú egyenlet legkorábbi ismert levezetése valójában az angliai Royal Military Academy atWoolwichben történt 1813-ban,és fegyverkutatásra használták.
Szakaszok
A sorozatosan toló rakétafokozatok esetében az egyenlet minden egyes fokozatra érvényes, ahol minden egyes fokozat esetében az egyenletben szereplő kezdeti tömeg a rakéta teljes tömege az előző fokozat elhagyása után, a végső tömeg pedig a rakéta teljes tömege közvetlenül az adott fokozat elhagyása előtt. Az egyes fokozatok esetében a fajlagos impulzus eltérő lehet.
Ha például a rakéta tömegének 80%-a az első fokozat üzemanyaga, 10%-a az első fokozat száraz tömege, 10%-a pedig a maradék rakéta, akkor
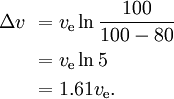
Három hasonló, később kisebb szakasz esetén, ahol minden szakaszhoz ugyanaz a ve tartozik, akkor
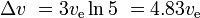
és a hasznos teher a kezdeti tömeg 10%*10%*10% = 0,1%-a.
Egy hasonló SSTO rakéta, szintén 0,1%-os hasznos teherrel, az üzemanyagtartályok és hajtóművek tömege 11%, az üzemanyagé pedig 88,9%. Ez azt eredményezné
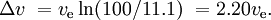
Ha egy új fokozat motorját még azelőtt begyújtják, hogy az előző fokozatot eldobták volna, és az egyidejűleg működő motorok eltérő fajlagos impulzusúak (ahogy ez gyakran előfordul a szilárd rakétahajtóművek és a folyékony üzemanyaggal működő fokozatok esetében), a helyzet bonyolultabb.
Energia
Az ideális esetben m1a hasznos hasznos teher és m0 – m1a reakciótömeg (ez megfelel a tömeg nélküli üres tartályoknak,stb.). A szükséges energia egyszerűen kiszámítható
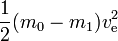
Ez megfelel annak a mozgási energiának, amellyel a kilökött reakciótömeg a kipufogógáz sebességével megegyező sebességnél rendelkezne. Ha a reakciótömeget a nulla sebességről a kilövési sebességre kellene gyorsítani, akkor az összes előállított energia a reakciótömegbe menne, és semmi sem maradna a rakéta és a hasznos teher mozgási energiájának növelésére. Ha azonban a rakéta már mozog és gyorsul (a reakciótömeg a rakéta mozgási irányával ellentétes irányba lökődik ki), kevesebb kinetikus energia kerül a reakciótömeghez. Ennek érzékeltetésére, ha például ve=10 km/s és a rakéta sebessége 3 km/s, akkor egy kis mennyiségű kilökött reakciótömeg sebessége 3 km/s-ról 7 km/s-ra változik előrefelé. Így, míg a szükséges energia 50 MJ/kg reakciótömeg, a reakciótömeg sebességnövekedéséhez csak 20 MJ kerül felhasználásra. A fennmaradó 30 MJ a rakéta és a hasznos teher mozgási energiájának növekedését jelenti.
Általánosságban:
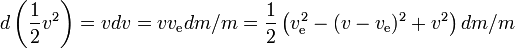
Így a rakéta fajlagos energianyeresége bármely kis időintervallumban a rakéta energianyeresége a maradék üzemanyaggal együtt,osztva a tömegével, ahol az energianyereség egyenlő az üzemanyag által termelt energiával mínusz a reakciótömeg energianyereségével. Minél nagyobb a rakéta sebessége, annál kisebb a reakciótömeg energianyeresete; ha a rakéta sebessége több mint a kipufogógázsebesség fele, a reakciótömeg még energiát is veszít a kilövéskor, a rakéta energianyereségének javára; minél nagyobb a rakéta sebessége, annál nagyobb a reakciótömeg energiavesztesége.
Megvan
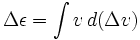
ahol ε a rakéta fajlagos energiája (potenciális és mozgási energia) és Δvis egy külön változó, nem csak a v változása.Abban az esetben, ha a rakétát lassításra használjuk, azaz a reakciótömeget a sebesség irányába lökjük ki, v negatívnak kell venni.
A képlet ismét az ideális esetre vonatkozik, ahol nem veszik el energia a hő stb. miatt. Ez utóbbi a tolóerő csökkenését okozza, így még akkor is előnytelen, ha a cél az energiaveszteség (lassulás).
Ha az energiát maga a tömeg termeli, mint egy kémiai rakétában, akkor az üzemanyagértéknek 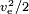 kell lennie, ahol az üzemanyagértéknél az oxidálószer tömegét is figyelembe kell venni. Egy tipikus érték ve= 4,5 km/s, ami 10,1 MJ/kg üzemanyagértéknek felel meg. A tényleges üzemanyagérték magasabb, de az energia nagy része a kipufogógázban hulladékhő formájában elvész, amelyet a fúvóka nem tudott kivonni.
kell lennie, ahol az üzemanyagértéknél az oxidálószer tömegét is figyelembe kell venni. Egy tipikus érték ve= 4,5 km/s, ami 10,1 MJ/kg üzemanyagértéknek felel meg. A tényleges üzemanyagérték magasabb, de az energia nagy része a kipufogógázban hulladékhő formájában elvész, amelyet a fúvóka nem tudott kivonni.
A szükséges energia E a
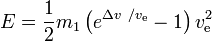
Következtetések:
- a
 esetén
esetén 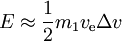
- adott Δv esetén a minimálisenergiára akkor van szükség, ha ve =0.6275Δv, amihez
E = 0,772m1(Δv)2 energiára van szükség. Nulla sebességről indulva ez 54,4 %-kal több, mint a hasznos teher kinetikus energiája. Ebben az optimális esetben a kezdeti tömeg4,92-szerese a végső tömegnek.
Ezek az eredmények rögzített kipufogógázsebességre vonatkoznak.
Az Oberth-effektus miatt és nem nulla sebességről indulva a hajtóanyagból szükséges potenciális energia kisebb lehet, mint a jármű és a hasznos teher energiájának növekedése. Ez akkor fordulhat elő, ha a reakciótömeg kilövés után kisebb sebességgel halad, mint előtte – a rakéták képesek a hajtóanyag kezdeti kinetikus energiájának egy részét vagy egészét felszabadítani.
Egy adott cél, például az egyik pályáról a másikra való elmozdulás esetén a szükséges Δv nagyban függhet attól a sebességtől, amellyel a hajtómű Δv-t tud produkálni, és a manőverek akár lehetetlenek is lehetnek, ha ez a sebesség túl alacsony. Például egy LEO-ra történő indításhoz általában kb. 9,5 km/s Δv szükséges (főleg a sebesség eléréséhez), de ha a hajtómű csak valamivel több mint g sebességgel tudna Δv-t produkálni, akkor ez egy lassú indítás lenne, ami összességében nagyon nagy Δv-t igényel (gondoljunk a lebegésre anélkül, hogy bármilyen sebesség- vagy magassági előrehaladást érnénk el, ez másodpercenként 9,8 m/s-os Δv-be kerülne). Ha a lehetséges sebesség csak g vagy annál kisebb, a manőver egyáltalán nem hajtható végre ezzel a hajtóművel.
A teljesítményt a következő képlet adja
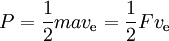
ahol F a tolóerő és a az ennek köszönhető gyorsulás. Így az egységnyi teljesítményre jutó elméletileg lehetséges tolóerő 2 osztva a m/s-ban kifejezett fajlagos impulzussal. A tolóerő hatásfok az ennek százalékában kifejezett tényleges tolóerő.
Ha pl. napenergiát használnak, ez korlátozza a-t; nagy ve esetén a lehetséges gyorsulás fordítottan arányos vele, ezért a szükséges delta-v eléréséhez szükséges idő arányos ve-vel;100 %-os hatásfokkal:
- a
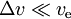 esetén
esetén 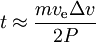
Példák:
- teljesítmény 1000 W, tömeg 100 kg, Δv=5 km/s, ve=16 km/s, tart 1.5 months.
- power 1000 W, mass 100 kg, Δv=5 km/s, ve=50 km/s, takes 5 months.
Thus ve should notbe too large.
Derivation
Consider the following system:
In the following derivation, “the rocket” is taken to mean “therocket and all of its unburned propellant”. Newton’s second law ofmotion relates external forces (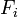 )to the change in linear momentum of the system as follows:
)to the change in linear momentum of the system as follows:
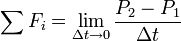
where 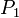 is the momentum of the rocket at time t=0:
is the momentum of the rocket at time t=0:
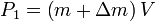
and 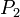 is the momentum of the rocket and exhausted mass at time
is the momentum of the rocket and exhausted mass at time  :
:
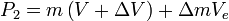
and where, with respect to the observer:
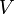 is thevelocity of the rocket at time t=0
is thevelocity of the rocket at time t=0
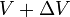 is thevelocity of the rocket at time
is thevelocity of the rocket at time 
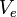 is thevelocity of the mass added to the exhaust (and lost by therocket) during time
is thevelocity of the mass added to the exhaust (and lost by therocket) during time 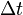
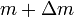 is the massof the rocket at time t=0
is the massof the rocket at time t=0
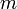 is the massof the rocket at time
is the massof the rocket at time 
The velocity of the exhaust Vein the observer frame is related to the velocity of the exhaust in therocket frame veby
Ve = V − ve
Solving yields:
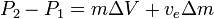
and
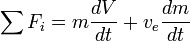
If there are no external forces then 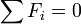 and
and
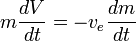
Feltéve 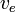 állandó, ezt integrálva megkapjuk:
állandó, ezt integrálva megkapjuk:
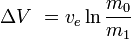
vagy egyenértékűen
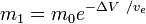 vagy
vagy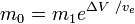
ahol m0 a kezdeti teljes tömeg a hajtóanyaggal együtt, és m1a végső össztömeg és veta rakéta kipufogógázának a rakétához viszonyított sebessége (a fajlagos impulzus, vagy, ha időben mérjük, akkor ez megszorozva a földi gravitációs gyorsulással).
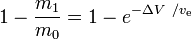 a tömeghányad (a kezdeti össztömegnek a reakciótömegként felhasznált része).
a tömeghányad (a kezdeti össztömegnek a reakciótömegként felhasznált része).
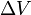 (delta v) a rakétahajtómű használata által keltett gyorsulás nagyságának időbeli integrálása (mi lenne a tényleges gyorsulás, ha nem lennének külső erők). A szabad térben, a sebesség irányában történő gyorsulás esetén ez a sebesség növekedése. Az ellenkező irányú gyorsulás (lassulás) esetén ez a sebesség csökkenése.
(delta v) a rakétahajtómű használata által keltett gyorsulás nagyságának időbeli integrálása (mi lenne a tényleges gyorsulás, ha nem lennének külső erők). A szabad térben, a sebesség irányában történő gyorsulás esetén ez a sebesség növekedése. Az ellenkező irányú gyorsulás (lassulás) esetén ez a sebesség csökkenése.
A gravitáció és a légellenállás természetesen szintén gyorsítja a járművet, és ezek hozzáadhatnak vagy levonhatnak a jármű által tapasztalt sebességváltozásból.
A delta-v tehát általában nem a jármű tényleges sebességváltozását vagy sebességét jelenti.
A rakétaegyenlet – bár szélsőséges egyszerűsítés – egyetlen rövid egyenletben foglalja össze a rakétarepülés fizikájának lényegét. Az is előfordul, hogy a delta-v az egyik legfontosabb mennyiség a pályamechanikában, amely számszerűsíti, hogy mennyire nehéz egy adott pályamanővert végrehajtani.
A nagy delta-v eléréséhez nyilvánvaló, hogy vagy m0-nak hatalmasnak kell lennie (a delta-v növekedésével exponenciálisan nő), vagy m1-nek kicsinek kell lennie, vagy ve-nek nagyon nagynak kell lennie, vagy ezek valamilyen kombinációjának.
A gyakorlatban ezt nagyon nagy rakéták (növekvő m0), több fokozat (csökkenő m1) és nagyon nagy kipufogógázsebességű rakéták alkalmazásával érték el. Az Apollo űrprogramban használt Saturn V rakéták és a hosszú távú pilóta nélküli szondákban használt ionhajtóművek jó példák erre.
A rakétaegyenlet az m1 tömeg egyfajta “exponenciális csökkenését” mutatja, nem az idő, hanem az előállított delta-v függvényében. A delta-v, amely a megfelelő “felezési idő”, 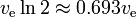
Példák
Tegyük fel, hogy a kilövési sebesség 4,5 km/s és a Δv 9,7 km/s (Föld-LEO).
- Egyfokozatú rakéta pályára állítása: 1 – e – 9,7 / 4,5= 0,884, tehát a kezdeti össztömeg 88,4 %-ának kell lennie hajtóanyagnak. A fennmaradó 11,6 % a hajtóművek, a tartály és a hasznos teher. Egy űrsikló esetében ez magában foglalja a pályára állítót is.
- Kétfokozatú pályára állítás: tegyük fel, hogy az első fokozatnak 5,0 km/s Δv-t kell biztosítania; 1 – e – 5,0 / 4,5= 0,671, tehát a kezdeti össztömeg 67,1%-a kell, hogy legyen hajtóanyag az első fokozathoz. A fennmaradó tömeg 32,9 %. Az első fokozat eltávolítása után az első fokozat tömegének maradványa megegyezik ezzel a 32 tömeggel.9 %, mínusz az első fokozat tartályának és hajtóműveinek tömege. Tegyük fel, hogy ez a kezdeti össztömeg 8 %-a, akkor 24,9 % marad. A második fokozatnak 4,7 km/s Δv-t kell biztosítania; 1 – e – 4,7 / 4,5= 0,648, tehát a fennmaradó tömeg 64,8 %-a kell, hogy legyen hajtóanyag, ami 16,2 %, és 8,7 % marad a második fokozat tartályára és hajtóműveire, a hasznos teherre, és egy űrsikló esetében a keringőegységre is. Így együttesen 16,7 % áll rendelkezésre az összes hajtóműre, a tartályokra, a hasznos teherre és az esetleges orbiterre.
Alkalmazhatóság
A rakétaegyenlet igaz a rakétaszerű reakciójárművekre, amikor a tényleges kipufogógázsebesség állandó; és összegezhető vagy integrálható, amikor a tényleges kipufogógázsebesség változik.
Az egyenlet azonban nem alkalmazható más technológiákra, például ágyúkilövőkre, űrliftekre, kilövőhurokra, kötélhajtóművekre és léghajtóművekre.
Lásd még
- Delta-v
- Delta-v költségvetés
- Oberth-effektus alkalmazása delta-v in a gravitywell increases the final velocity
- Specific impulse
- Spacecraft propulsion
- Mass ratio
- Working mass
- Relativistic rocket
- Reversibility oforbits
|
|
This article includes a list of references, but itssources remain unclear because it has insufficient inline citations. Please help to improvethis article by introducing more precise citations where appropriate. (February2009) |
- ^К. Э. Циолковский, Исследование мировых пространств реактивнымиприборами, 1903. It is available online here in a RARed PDF
- ^ Moore, William; ofthe MilitaryAcademy at Woolwich (1813). A Treatise on the Motion ofRockets. To which is added, An Essay on Naval Gunnery. London: G.and S. Robinson.
- ^ Johnson, W. (1995). “Contents and commentary onWilliam Moore’s a treatise on the motion of rockets and an essay onnaval gunnery”. International Journal of Impact Engineering 16 (3): 499–521. doi:10.1016/0734-743X(94)00052-X. ISSN 0734-743X. http://www.sciencedirect.com/science/article/B6V3K-3Y5FP5P-11/2/c3e98a6cec8f083c93dc4e4e157282bb.
- How to derive the rocket equation
- Relativity Calculator – LearnTsiolkovsky’s rocket equations