| Astrodynamics | ||
| Orbital mechanics | Equations | Efficiencymeasures |
|---|---|---|
| v · d · e |
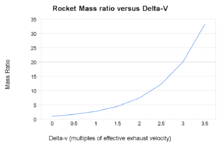
Rapporti di massa del razzo rispetto alla velocità finale calcolata dall’equazione del razzo
L’equazione di Tsiolkovsky del razzo, o equazione ideale del razzo, è un’equazione matematica che mette in relazione il delta-v (il massimo cambiamento di velocità del razzo se non agiscono altre forze esterne) con la velocità effettiva di scarico e la massa iniziale e finale di un razzo o di un altro motore a reazione.
L’equazione prende il nome da Konstantin Tsiolkovsky che la derivò indipendentemente e la pubblicò nel suo lavoro del 1903. Considera il principio di un razzo: un dispositivo che può applicare un’accelerazione a se stesso (una spinta) espellendo parte della sua massa con alta velocità nella direzione opposta per la conservazione della quantità di moto.
Per qualsiasi manovra di questo tipo (o per un viaggio che implichi una serie di manovre di questo tipo):
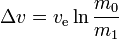
where:
m0 is the initialtotal mass, including propellant. m1 is the finaltotal mass. ve is the effectiveexhaust velocity. (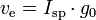 where Isp is the specific impulse expressed as a timeperiod)
where Isp is the specific impulse expressed as a timeperiod)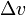 is delta-v-the maximum change of speed of the vehicle (with noexternal forces acting)
is delta-v-the maximum change of speed of the vehicle (with noexternal forces acting)
Units used for mass or velocity do not matter as long as they areconsistent.
- 1 History
- 2 Stages
- 3 Energy
- 4 Derivation
- 5 Examples
- 6 Applicability
- 7 See also
- 8 References
- 9 External links
History
This equation was independently derived by Konstantin Tsiolkovsky towards theend of the 19th century and is widely known under this name and idealrocket equation. Tuttavia, un opuscolo recentemente scoperto “A Treatiseon the Motion of Rockets” di William Mooreshows mostra che la prima derivazione conosciuta di questo tipo di equazione fu in realtà alla Royal Military Academy di Woolwich in Inghilterra nel 1813, e fu usata per la ricerca sulle armi.
Stadi
Nel caso di stadi di razzi a spinta sequenziale, l’equazione si applica per ogni stadio, dove per ogni stadio la massa iniziale nell’equazione è la massa totale del razzo dopo aver scartato lo stadio precedente, e la massa finale nell’equazione è la massa totale del razzo appena prima di scartare lo stadio interessato. Per ogni stadio l’impulso specifico può essere diverso.
Per esempio, se l’80% della massa di un razzo è il combustibile del primo stadio, e il 10% è la massa secca del primo stadio, e il 10% è il razzo rimanente, allora
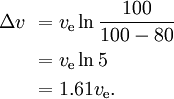
Con tre stadi simili e successivamente più piccoli con la stessa v per ogni stadio, abbiamo
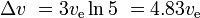
e il carico utile è 10%*10%*10% = 0,1% della massa iniziale.
Un razzo SSTO comparabile, sempre con un carico utile dello 0,1%, potrebbe avere una massa dell’11% per i serbatoi e i motori, e dell’88,9% per il carburante. Questo darebbe
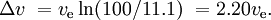
Se il motore di un nuovo stadio viene acceso prima che lo stadio precedente sia stato scartato e i motori che lavorano simultaneamente hanno un impulso specifico diverso (come spesso accade nei razzi a propellente solido e negli stadi a combustibile liquido), la situazione è più complicata.
Energia
Nel caso ideale m1 è il carico utile e m0 – m1 è la massa di reazione (questo corrisponde a serbatoi vuoti che non hanno massa, ecc.) L’energia richiesta può essere semplicemente calcolata come
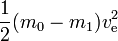
Questa corrisponde all’energia cinetica che la massa di reazione espulsa avrebbe ad una velocità pari a quella di scarico. Se la massa di reazione dovesse essere accelerata da velocità zero alla velocità di scarico, tutta l’energia prodotta andrebbe nella massa di reazione e non rimarrebbe nulla per il guadagno di energia cinetica del razzo e del carico utile. Tuttavia, se il razzo si muove già e accelera (la massa di reazione viene espulsa nella direzione opposta a quella in cui si muove il razzo) viene aggiunta meno energia cinetica alla massa di reazione. Per vedere questo, se, per esempio, ve=10 km/s e la velocità del razzo è 3 km/s, allora la velocità di una piccola quantità di massa di reazione espulsa cambia da 3 in avanti a 7 km/s indietro. Così, mentre l’energia richiesta è di 50 MJ per kg di massa di reazione, solo 20 MJ sono usati per l’aumento di velocità della massa di reazione. I restanti 30 MJ sono l’aumento dell’energia cinetica del razzo e del carico utile.
In generale:
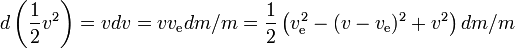
Quindi il guadagno di energia specifica del razzo in qualsiasi piccolo intervallo di tempo è il guadagno di energia del razzo compreso il carburante rimanente,diviso per la sua massa, dove il guadagno di energia è uguale all’energia prodotta dal combustibile meno il guadagno di energia della massa di reazione. Più grande è la velocità del razzo, minore è il guadagno di energia della massa di reazione; se la velocità del razzo è più della metà della velocità di scarico, la massa di reazione perde addirittura energia quando viene espulsa, a vantaggio del guadagno di energia del razzo; più grande è la velocità del razzo, maggiore è la perdita di energia della massa di reazione.
Abbiamo
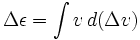
dove ε è l’energia specifica del razzo (energia potenziale più cinetica) e Δvis una variabile separata, non solo la variazione di v.Nel caso di usare il razzo per la decelerazione, cioè per espellere la massa di reazione nella direzione della velocità, v dovrebbe essere preso negativo.
La formula è ancora per il caso ideale, senza energia persa per il calore, ecc. Quest’ultima causa una riduzione della spinta, quindi è un vantaggio anche quando l’obiettivo è quello di perdere energia (decelerazione).
Se l’energia è prodotta dalla massa stessa, come in un razzo chimico, il valore del carburante deve essere 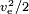 , dove per il valore del carburante anche la massa dell’ossidante deve essere presa in considerazione. Un valore tipico è ve= 4,5 km/s, corrispondente ad un valore di carburante di 10,1 MJ/kg. Il valore effettivo del combustibile è più alto, ma gran parte dell’energia viene persa come calore residuo nello scarico che l’ugello non è stato in grado di estrarre.
, dove per il valore del carburante anche la massa dell’ossidante deve essere presa in considerazione. Un valore tipico è ve= 4,5 km/s, corrispondente ad un valore di carburante di 10,1 MJ/kg. Il valore effettivo del combustibile è più alto, ma gran parte dell’energia viene persa come calore residuo nello scarico che l’ugello non è stato in grado di estrarre.
L’energia richiesta E è
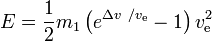
Conclusioni:
- per
 abbiamo
abbiamo 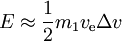
- per un dato Δv, la minima energia è necessaria se ve =0.6275Δv, richiedendo un’energia di
E = 0,772m1(Δv)2. Partendo da velocità zero questo è il 54,4% in più della sola energia cinetica del carico utile. In questo caso ottimale la massa iniziale è 4,92 volte la massa finale.
Questi risultati valgono per una velocità di scarico fissa.
A causa dell’effetto Oberth, e partendo da una velocità non zero l’energia potenziale necessaria al propellente può essere inferiore all’aumento di energia nel veicolo e nel carico utile. Questo può essere il caso quando la massa di reazione ha una velocità inferiore dopo essere stata espulsa rispetto a prima – i razzi sono in grado di liberare parte o tutta l’energia cinetica iniziale del propellente.
Inoltre, per un dato obiettivo come lo spostamento da un’orbita all’altra, il Δv richiesto può dipendere notevolmente dal tasso al quale il motore può produrre Δv e le manovre possono anche essere impossibili se tale tasso è troppo basso. Per esempio, un lancio verso LEO richiede normalmente un Δv di circa 9,5 km/s (soprattutto per la velocità da acquisire), ma se il motore potesse produrre Δv a un tasso di solo poco più di g, sarebbe un lancio lento che richiede complessivamente un Δv molto grande (si pensi di librarsi senza fare alcun progresso in velocità o altitudine, costerebbe un Δvo di 9,8 m/s ogni secondo). Se la velocità possibile è solo g o meno, la manovra non può essere eseguita affatto con questo motore.
La potenza è data da
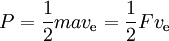
dove F è la spinta e a l’accelerazione dovuta. Così la spinta teoricamente possibile per unità di potenza è 2 diviso l’impulso specifico in m/s. L’efficienza della spinta è la spinta effettiva come percentuale di questa.
Se per esempio se si usa l’energia solare, questo limita a; nel caso di una grande ve l’accelerazione possibile è inversamente proporzionale ad essa, quindi il tempo per raggiungere un delta-v richiesto è proporzionale a ve; con un’efficienza del 100%:
- per
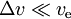 abbiamo
abbiamo 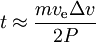
Esempi:
- potenza 1000 W, massa 100 kg, Δv=5 km/s, ve=16 km/s, richiede 1.5 months.
- power 1000 W, mass 100 kg, Δv=5 km/s, ve=50 km/s, takes 5 months.
Thus ve should notbe too large.
Derivation
Consider the following system:
In the following derivation, “the rocket” is taken to mean “therocket and all of its unburned propellant”. Newton’s second law ofmotion relates external forces (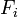 )to the change in linear momentum of the system as follows:
)to the change in linear momentum of the system as follows:
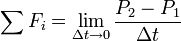
where 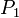 is the momentum of the rocket at time t=0:
is the momentum of the rocket at time t=0:
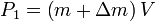
and 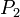 is the momentum of the rocket and exhausted mass at time
is the momentum of the rocket and exhausted mass at time  :
:
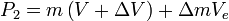
and where, with respect to the observer:
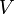 is thevelocity of the rocket at time t=0
is thevelocity of the rocket at time t=0
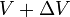 is thevelocity of the rocket at time
is thevelocity of the rocket at time 
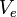 is thevelocity of the mass added to the exhaust (and lost by therocket) during time
is thevelocity of the mass added to the exhaust (and lost by therocket) during time 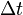
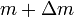 is the massof the rocket at time t=0
is the massof the rocket at time t=0
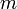 is the massof the rocket at time
is the massof the rocket at time 
The velocity of the exhaust Vein the observer frame is related to the velocity of the exhaust in therocket frame veby
Ve = V − ve
Solving yields:
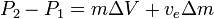
and
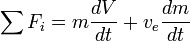
If there are no external forces then 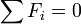 and
and
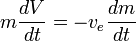
Assumendo che 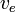 sia costante, questo può essere integrato per ottenere:
sia costante, questo può essere integrato per ottenere:
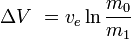
o equivalentemente
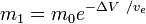 o
o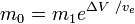
dove m0 è la massa totale iniziale incluso il propellente, e m1 la massa totale finale e vet la velocità dello scarico del razzo rispetto al razzo (l’impulso specifico, o, se misurato in tempo, quello moltiplicato per l’accelerazione gravità-terra).
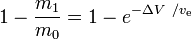 è la frazione di massa (la parte della massa totale iniziale che viene spesa come massa di reazione).
è la frazione di massa (la parte della massa totale iniziale che viene spesa come massa di reazione).
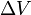 (delta v) è l’integrazione nel tempo della grandezza dell’accelerazione prodotta dall’uso del motore a razzo (quale sarebbe l’accelerazione reale se le forze esterne fossero assenti). Nello spazio libero, per il caso di accelerazione nella direzione della velocità, questo è l’aumento della velocità. Nel caso di un’accelerazione in direzione opposta (decelerazione) è la diminuzione della velocità.
(delta v) è l’integrazione nel tempo della grandezza dell’accelerazione prodotta dall’uso del motore a razzo (quale sarebbe l’accelerazione reale se le forze esterne fossero assenti). Nello spazio libero, per il caso di accelerazione nella direzione della velocità, questo è l’aumento della velocità. Nel caso di un’accelerazione in direzione opposta (decelerazione) è la diminuzione della velocità.
Ovviamente anche la gravità e la resistenza accelerano il veicolo, e possono aggiungere o sottrarre al cambiamento di velocità sperimentato dal veicolo.
Quindi il delta-v non è di solito il cambiamento effettivo di velocità o velocità del veicolo.
Anche se una semplificazione estrema, l’equazione del razzo cattura l’essenziale della fisica del volo a razzo in una singola breve equazione. Si dà anche il caso che il delta-v sia una delle più importanti quantità nella meccanica orbitale, che quantifica quanto sia difficile eseguire una data manovra orbitale.
E’ chiaro che per ottenere un grande delta-v, o m0 deve essere enorme (crescendo esponenzialmente quando il delta-v sale), o m1 deve essere minuscolo, o ve deve essere molto alto, o qualche combinazione di tutte queste.
In pratica, questo è stato ottenuto usando razzi molto grandi (aumentando m0), con stadi multipli (diminuendo m1), e razzi con velocità di scarico molto alte. I razzi Saturn V usati nel programma spaziale Apollo e i propulsori ionici usati nelle sonde senza equipaggio a lunga distanza sono buoni esempi di questo.
L’equazione del razzo mostra una sorta di “decadimento esponenziale” della massa m1, non in funzione del tempo, ma in funzione del delta-v prodotto. Il delta-v che è il corrispondente “tempo di dimezzamento” è 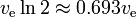
Esempi
Assumiamo una velocità di scarico di 4,5 km/s e un Δv di 9,7 km/s (dalla Terra a LEO).
- Singolo stadio al razzo orbitante: 1 – e – 9.7 / 4.5= 0.884, quindi l’88.4 % della massa totale iniziale deve essere propellente. Il restante 11,6% è per i motori, il serbatoio e il carico utile. Nel caso di una navetta spaziale, includerebbe anche l’orbiter.
- Due stadi in orbita: supponiamo che il primo stadio debba fornire un Δvo di 5,0 km/s; 1 – e – 5,0 / 4,5= 0,671, quindi il 67,1% della massa totale iniziale deve essere propellente al primo stadio. La massa rimanente è il 32,9%. Dopo lo smaltimento del primo stadio, rimane una massa pari a questa 32.9 %, meno la massa del serbatoio e dei motori del primo stadio. Supponiamo che questo sia l’8% della massa totale iniziale, quindi rimane il 24,9%. Il secondo stadio dovrebbe fornire un Δvo di 4,7 km/s; 1 – e – 4,7 / 4,5 = 0,648, quindi il 64,8% della massa rimanente deve essere propellente, che è il 16,2%, e l’8,7% rimane per il serbatoio e i motori del secondo stadio, il carico utile, e nel caso di una navetta spaziale, anche l’orbiter. Così insieme il 16,7% è disponibile per tutti i motori, i serbatoi, il carico utile e l’eventuale orbiter.
Applicabilità
L’equazione del razzo vale per i veicoli a reazione tipo razzo ogni volta che la velocità effettiva di scarico è costante; e può essere sommata o integrata quando la velocità effettiva di scarico varia.
Tuttavia, non si applica ad altre tecnologie come i gunlaunch, gli elevatori spaziali, i launchloop, la propulsione tether e i motori a soffio d’aria.
Vedi anche
- Delta-v
- Delta-v budget
- Effetto Oberth applicando delta-v in a gravitywell increases the final velocity
- Specific impulse
- Spacecraft propulsion
- Mass ratio
- Working mass
- Relativistic rocket
- Reversibility oforbits
|
|
This article includes a list of references, but itssources remain unclear because it has insufficient inline citations. Please help to improvethis article by introducing more precise citations where appropriate. (February2009) |
- ^К. Э. Циолковский, Исследование мировых пространств реактивнымиприборами, 1903. It is available online here in a RARed PDF
- ^ Moore, William; ofthe MilitaryAcademy at Woolwich (1813). A Treatise on the Motion ofRockets. To which is added, An Essay on Naval Gunnery. London: G.and S. Robinson.
- ^ Johnson, W. (1995). “Contents and commentary onWilliam Moore’s a treatise on the motion of rockets and an essay onnaval gunnery”. International Journal of Impact Engineering 16 (3): 499–521. doi:10.1016/0734-743X(94)00052-X. ISSN 0734-743X. http://www.sciencedirect.com/science/article/B6V3K-3Y5FP5P-11/2/c3e98a6cec8f083c93dc4e4e157282bb.
- How to derive the rocket equation
- Relativity Calculator – LearnTsiolkovsky’s rocket equations