| Astrodynamics | ||
| Orbital mechanics | Equations | Efficiencymeasures |
|---|---|---|
| v · d · e |
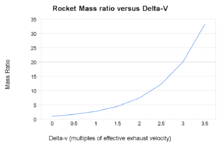
Raketmassakvoter mot sluthastighet beräknat utifrån raketekvationen
Tsiolkovskijs raketekvation, är en matematisk ekvation som relaterar delta-v (raketens maximala hastighetsförändring om inga andra yttre krafter verkar) till den effektiva utloppshastigheten och den initiala och slutliga massan hos en raket eller annan reaktionsmotor.
Ekvationen är uppkallad efter Konstantin Tsiolkovskij, som självständigt tog fram den och publicerade den i sitt arbete från 1903.I ekvationen beaktas principen för en raket: en anordning som kan ge sig själv en acceleration (en dragkraft) genom att en del av sin massa skjuts ut med hög hastighet i motsatt riktning på grund av rörelsemängdens bevarande.
För varje sådan manöver (eller resa som omfattar ett antal sådana manövrar):
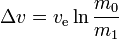
where:
m0 is the initialtotal mass, including propellant. m1 is the finaltotal mass. ve is the effectiveexhaust velocity. (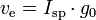 where Isp is the specific impulse expressed as a timeperiod)
where Isp is the specific impulse expressed as a timeperiod) 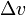 is delta-v-the maximum change of speed of the vehicle (with noexternal forces acting)
is delta-v-the maximum change of speed of the vehicle (with noexternal forces acting)
Units used for mass or velocity do not matter as long as they areconsistent.
Contents
- 1 History
- 2 Stages
- 3 Energy
- 4 Derivation
- 5 Examples
- 6 Applicability
- 7 See also
- 8 References
- 9 External links
History
This equation was independently derived by Konstantin Tsiolkovsky towards theend of the 19th century and is widely known under this name and idealrocket equation. En nyligen upptäckt pamflett ”A Treatiseon the Motion of Rockets” av William Moor visar dock att den tidigaste kända härledningen av denna typ av ekvation faktiskt gjordes vid Royal Military Academy i Woolwich i England 1813 och användes för vapenforskning.
Steg
För raketsteg med sekventiell dragkraft gäller ekvationen för varje steg, där för varje steg den initiala massan i ekvationen är raketens totala massa efter att det föregående steget har kastats bort, och den slutliga massan i ekvationen är raketens totala massa precis innan det aktuella steget kastas bort. Den specifika impulsen kan vara olika för varje steg.
Om t.ex. 80 % av raketens massa utgörs av bränslet i det första steget, 10 % av den torra massan i det första steget och 10 % av den kvarvarande raketen, då
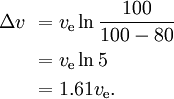
Med tre liknande, därefter mindre etapper med samma ve för varje etapp har vi
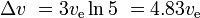
och nyttolasten är 10 %*10 %*10 % = 0,1 % av den ursprungliga massan.
En jämförbar SSTO-raket, också med 0,1 % nyttolast, skulle kunna ha en massa på 11 % för bränsletankar och motorer och 88,9 % för bränsle. Detta skulle ge
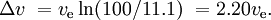
Om motorn i ett nytt steg antänds innan det föregående steget har kastats och de samtidigt arbetande motorerna har olika specifik impuls (vilket ofta är fallet med solid rocket boosters och aliquid-fuel stage) är situationen mer komplicerad.
Energi
I idealfallet är m1nyttig nyttolast och m0 – m1reaktionsmassa (detta motsvarar tomma tankar som inte har någon massa etc.). Den energi som krävs kan helt enkelt beräknas som
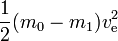
Detta motsvarar den kinetiska energi som den utdrivna reaktionsmassan skulle ha vid en hastighet som är lika med utloppshastigheten. Om reaktionsmassan skulle behöva accelereras från nollhastighet till utloppshastighet skulle all energi som produceras gå till reaktionsmassan och inget skulle finnas kvar för kinetisk energi till raket och nyttolast. Men om raketen redan rör sig och accelererar (reaktionsmassan utvisas i motsatt riktning mot den riktning som raketen rör sig i) tillförs mindre kinetisk energi till reaktionsmassan. För att se detta, om t.ex. ve=10 km/s och raketens hastighet är 3 km/s, ändras hastigheten för en liten mängd av den fördrivna reaktionsmassan från 3 km framåt till 7 km/s bakåt. Medan den energi som krävs är 50 MJ per kg reaktionsmassa används alltså endast 20 MJ för att öka reaktionsmassans hastighet. De återstående 30 MJ utgörs av ökningen av den kinetiska energin hos raketen och nyttolasten.
I allmänhet:
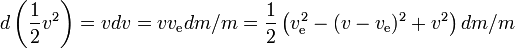
Därmed är raketens specifika energivinst under ett litet tidsintervall raketens energivinst inklusive det återstående bränslet,dividerat med dess massa, där energivinsten är lika med den energi som produceras av bränslet minus energivinsten från reaktionsmassan. Om raketens hastighet är mer än hälften av utloppshastigheten förlorar reaktionsmassan till och med energi när den utvisas, till förmån för raketens energivinst; ju större raketens hastighet, desto större energiförlust för reaktionsmassan.
Vi har
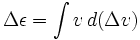
där ε är raketens specifika energi (potentiell plus kinetisk energi) och Δvis en separat variabel, inte bara förändringen i v.Om raketen används för att bromsa upp, dvs. för att utstöta reaktionsmassan i hastighetsriktningen, ska vs tas som negativ.
Formeln gäller återigen för det ideala fallet, utan att någon energi går förlorad på grund av värme osv. Det senare orsakar en minskning av dragkraften, så det är en nackdel även när målet är att förlora energi (retardation).
Om energin produceras av själva massan, som i en kemisk raket, måste bränslevärdet vara 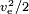 ,där för bränslevärdet även massan av oxidationsmedlet måste tas med i beräkningen. Ett typiskt värde är ve= 4,5 km/s, vilket motsvarar ett bränslevärde på 10,1 MJ/kg. Det faktiska bränslevärdet är högre, men en stor del av energin går förlorad som spillvärme i avgaserna som munstycket inte kunde utvinna.
,där för bränslevärdet även massan av oxidationsmedlet måste tas med i beräkningen. Ett typiskt värde är ve= 4,5 km/s, vilket motsvarar ett bränslevärde på 10,1 MJ/kg. Det faktiska bränslevärdet är högre, men en stor del av energin går förlorad som spillvärme i avgaserna som munstycket inte kunde utvinna.
Den nödvändiga energin E är
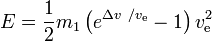
Slutsatser:
- för
 har vi
har vi 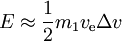
- För ett givet Δv behövs den minimala energin om ve = 0.6275Δv, vilket kräver en energi på
E = 0,772m1(Δv)2. Med utgångspunkt från nollfart är detta 54,4 % mer än bara nyttolastens kinetiska energi. I detta optimala fall är den ursprungliga massan 4,92 gånger den slutliga massan.
Dessa resultat gäller för en fast avgashastighet.
På grund av Oberth-effekten, och när man startar från en hastighet som inte är noll, kan den potentiella energi som krävs från drivmedlet vara mindre än ökningen av energin i fordonet och nyttolasten. Detta kan vara fallet när reaktionsmassan har en lägre hastighet efter utdrivningen än före – raketer kan frigöra en del av eller hela den ursprungliga kinetiska energin i drivmedlet.
För ett givet mål, t.ex. att förflytta sig från en omloppsbana till en annan, kan den erforderliga Δv i hög grad bero på den hastighet med vilken motorn kan producera Δv, och manövrar kan till och med vara omöjliga om denna hastighet är för låg. En uppskjutning till LEO kräver t.ex. normalt ett Δv på ca 9,5 km/s (främst för att uppnå den hastighet som krävs), men om motorn kan producera Δv med en hastighet på endast något mer än g skulle det bli en långsam uppskjutning som kräver ett mycket stort Δv (tänk att sväva i luften utan att göra några framsteg i hastighet eller höjd, det skulle kosta ett Δv på 9,8 m/s varje sekund). Om den möjliga hastigheten endast är g eller mindre kan manövern inte genomföras alls med denna motor.
Effekten ges av
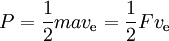
där F är dragkraften och a den acceleration som beror på den. Den teoretiskt möjliga dragkraften per effektenhet är således 2 dividerat med den specifika impulsen i m/s. Skjutkraftseffektiviteten är den faktiska skjutkraften i procent av denna.
Om t.ex. Om man t.ex. använder solenergi begränsar detta a; vid en stor ve är den möjliga accelerationen omvänt proportionell mot den, och därför är tiden för att nå en erforderligdelta-v proportionell mot ve; med 100 % verkningsgrad:
- för
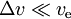 har vi
har vi 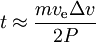
Exempel:
- effekt 1000 W, massa 100 kg, Δv=5 km/s, ve=16 km/s, tar 1.5 months.
- power 1000 W, mass 100 kg, Δv=5 km/s, ve=50 km/s, takes 5 months.
Thus ve should notbe too large.
Derivation
Consider the following system:
In the following derivation, ”the rocket” is taken to mean ”therocket and all of its unburned propellant”. Newton’s second law ofmotion relates external forces (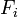 )to the change in linear momentum of the system as follows:
)to the change in linear momentum of the system as follows:
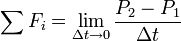
where 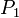 is the momentum of the rocket at time t=0:
is the momentum of the rocket at time t=0:
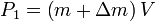
and 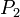 is the momentum of the rocket and exhausted mass at time
is the momentum of the rocket and exhausted mass at time  :
:
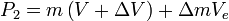
and where, with respect to the observer:
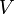 is thevelocity of the rocket at time t=0
is thevelocity of the rocket at time t=0
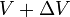 is thevelocity of the rocket at time
is thevelocity of the rocket at time 
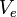 is thevelocity of the mass added to the exhaust (and lost by therocket) during time
is thevelocity of the mass added to the exhaust (and lost by therocket) during time 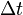
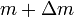 is the massof the rocket at time t=0
is the massof the rocket at time t=0
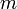 is the massof the rocket at time
is the massof the rocket at time 
The velocity of the exhaust Vein the observer frame is related to the velocity of the exhaust in therocket frame veby
Ve = V − ve
Solving yields:
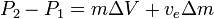
and
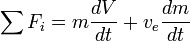
If there are no external forces then 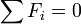 and
and
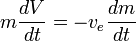
Att anta 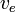 är konstant, kan detta integreras för att ge:
är konstant, kan detta integreras för att ge:
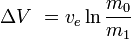
eller motsvarande
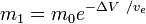 eller
eller 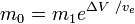
där m0 är den ursprungliga totala massan, inklusive drivmedel, och m1den slutliga totala massan och vethastigheten hos raketens avgasutsläpp i förhållande till raketen (den specifika impulsen eller, om den mäts i tid, den multiplicerad med jordens gravitationsacceleration).
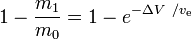 är massafraktionen (den del av den ursprungliga totala massan som används som reaktionsmassa).
är massafraktionen (den del av den ursprungliga totala massan som används som reaktionsmassa).
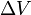 (delta v) är integrationen över tiden av storleken på den acceleration som produceras genom att använda raketmotorn (vad som skulle vara den faktiska accelerationen om inga yttre krafter fanns). I fria rymden, för fallet med acceleration i hastighetsriktningen, är detta ökningen av hastigheten. Vid acceleration i motsatt riktning (retardation) är det hastighetsminskningen.
(delta v) är integrationen över tiden av storleken på den acceleration som produceras genom att använda raketmotorn (vad som skulle vara den faktiska accelerationen om inga yttre krafter fanns). I fria rymden, för fallet med acceleration i hastighetsriktningen, är detta ökningen av hastigheten. Vid acceleration i motsatt riktning (retardation) är det hastighetsminskningen.
Givetvis accelererar även gravitation och motstånd fordonet, och de kan lägga till eller dra ifrån den hastighetsförändring som fordonet upplever.Delta-v är därför vanligtvis inte den faktiska hastighetsförändringen för fordonet.
Raketekvationen är visserligen en extrem förenkling, men den fångar de viktigaste delarna av raketflygets fysik i en enda kort ekvation. Det är också så att delta-v är en av de viktigaste storheterna inom banmekaniken, som anger hur svårt det är att utföra en viss banmanöver.
För att uppnå ett stort delta-v måste antingen m0 vara enormt stort (och växa exponentiellt när delta-v ökar), eller så måste m1 vara liten, eller så måste ve vara mycket hög, eller en kombination av alla dessa.
I praktiken har man uppnått detta genom att använda mycket stora raketer (vilket ökar m0), med flera steg (vilket minskar m1) och raketer med mycket höga utloppshastigheter. Saturn V-raketerna som användes i Apollo-rymdprogrammet och de jonraketer som används i obemannade sonder på långa avstånd är goda exempel på detta.
Raketekvationen visar ett slags ”exponentiellt avtagande” av massan m1, inte som en funktion av tiden, utan som en funktion av det producerade delta-v. Delta-v som är den motsvarande ”halveringstiden” är 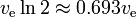
Exempel
Antag att utloppshastigheten är 4,5 km/s och Δv 9,7 km/s (jorden till LEO).
- Enstegsraket till bana: 1 – e – 9,7 / 4,5= 0,884, vilket innebär att 88,4 % av den ursprungliga totala massan måste utgöras av drivmedel. Resterande 11,6 % är för motorerna, tanken och nyttolasten. När det gäller en rymdfärja skulle den också omfattaorbiterna.
- Två steg till omloppsbana: anta att det första steget ska ge en Δvo på 5,0 km/s; 1 – e – 5,0 / 4,5= 0,671, vilket innebär att 67,1 % av den ursprungliga totala massan måste utgöras av drivmedel till det första steget. Den återstående massan är 32,9 %. Efter det att det första steget har avyttrats återstår en massa som är lika med dessa 32,9 %.9 %, minus massan av tanken och motorerna i det första steget. Om vi antar att detta är 8 % av den ursprungliga totala massan återstår 24,9 %. Det andra steget ska ge en Δvo på 4,7 km/s; 1 – e – 4,7 / 4,5= 0,648. Därför måste 64,8 % av den återstående massan utgöras av drivmedel, vilket är 16,2 %, och 8,7 % återstår för tanken och motorerna i det andra steget, för nyttolasten och, när det gäller en rymdfärja, även för omloppsbanan. Sammanlagt 16,7 % är alltså tillgängliga för alla motorer, tankarna, nyttolasten och den eventuella omloppsfarkosten.
Tillämplighet
Raketekvationen gäller för raketliknande reaktionsfordon när den effektiva utloppshastigheten är konstant, och kan summeras eller integreras när den effektiva utloppshastigheten varierar.
Den gäller dock inte för andra tekniker, t.ex. kanonlanseringar, rymdhissar, uppskjutningsslingor, tetherframdrivning och luftandningsmotorer.
Se även
- Delta-v
- Delta-v-budget
- Oberth-effekt som tillämpar delta-.v in a gravitywell increases the final velocity
- Specific impulse
- Spacecraft propulsion
- Mass ratio
- Working mass
- Relativistic rocket
- Reversibility oforbits
|
|
This article includes a list of references, but itssources remain unclear because it has insufficient inline citations. Please help to improvethis article by introducing more precise citations where appropriate. (February2009) |
- ^К. Э. Циолковский, Исследование мировых пространств реактивнымиприборами, 1903. It is available online here in a RARed PDF
- ^ Moore, William; ofthe MilitaryAcademy at Woolwich (1813). A Treatise on the Motion ofRockets. To which is added, An Essay on Naval Gunnery. London: G.and S. Robinson.
- ^ Johnson, W. (1995). ”Contents and commentary onWilliam Moore’s a treatise on the motion of rockets and an essay onnaval gunnery”. International Journal of Impact Engineering 16 (3): 499–521. doi:10.1016/0734-743X(94)00052-X. ISSN 0734-743X. http://www.sciencedirect.com/science/article/B6V3K-3Y5FP5P-11/2/c3e98a6cec8f083c93dc4e4e157282bb.
- How to derive the rocket equation
- Relativity Calculator – LearnTsiolkovsky’s rocket equations